Расчет на прочность при изгибе
При чистом изгибе в поперечных сечениях бачки возникают только нормальные напряжения 
. При поперечном изгибе, кроме нормальных напряжений, имеют место и касательные напряжения τ, которые, как и нормальные, распределены по высоте сечения неравномерно, что вызывает неравномерное распределение угловых деформаций 
. В результате поперечные сечения деплаиируют. Однако нарушение гипотезы плоских сечений незначительно влияет на величину нормальных напряжений. Поэтому формулы, полученные для определения нормальных напряжений при чистом изгибе, остаются справедливыми для определения этих напряжений и при поперечном изгибе.
Расчет на прочность балок из пластичных материалов.
Расчет на прочность осуществляют при изгибе по наибольшим нормальным напряжениям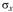 
. Возникающие в поперечных сечениях касательные напряжения не учитываются ввиду их малости по сравнению с нормальными напряжениями.
Сечение балки, в котором возникает наибольший по модулю момент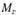 
, является расчетным (опасным). Наибольшие 
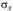возникают в волокнах, наиболее удаленных от нейтральной линии.
Условие прочности при изгибе имеет вид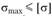 
. Для традиционных конструкционных материалов (стальные, алюминиевые, титановые и магниевые сплавы) допускаемые напряжения при изгибе
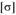принимаются такими же, как и при растяжении (сжатии).
Используя условие прочности, проектировочный расчет производят по формуле
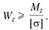(2.75)
Подставляя в выражение (2.75) соответствующее выражение для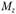
и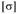
, определяют необходимые по условию прочности размеры сечения. Значения
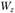конкретного сечения берутся по справочнику или вычисляются по соовет- ствующсй формуле.
В балках постоянного по длине сечения вес конструкции прямо пропорционален площади сечения А: чем больше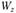
для данного А, тем рациональнее форма сечения. При изменении положения сечения относительно плоскости действия нагрузки прочность балки может существенно меняться за счет
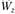, хотя А не изменится. Сечение следует ориентировать таким образом, чтобы изгиб балки проходил в плоскости наибольшей жесткости на изгиб
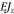. Например, прямоугольное сечение ориентируют длинной стороной параллельно плоскости изгибающего момента
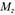, тогда
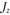и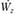
достигают наибольших значений.
Расчет на прочность балок из хрупких материалов. Хрупкие материалы, в отличие от пластичных, различно сопротивляются растяжению и сжатию, т.е. имеют различные значения допускаемых напряжений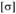 
па растяжение и сжатие. Поэтому для хрупких материалов целесообразно применять сечения, несимметричные относительно нейтральной линии, например тавровое, П-образное и др. При этом сечение следует ориентировать таким образом, чтобы его часть с меньшим находилась в растянутой зоне, поскольку на растяжение хрупкие материалы работают значительно хуже, чем на сжатие.
Касательные напряжения при изгибе
Касательные напряжения в сплошных сечениях. Будем считать, что при поперечном изгибе сохраняется гипотеза плоских сечений. Пусть консольная балка нагружена силой F (рис. 2.31). Определим касательные напряжения, действующие в горизонтальном сечении АВ, расположенном на расстоянии у от нейтральной оси. Для решения задачи используем закон парности касательных напряжений, позволяющий для определения касательных напряжений в поперечном сечении балки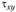 
рассматривать равные им по величине 
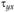, действующие в горизонтальной плоскости. Выделим элемент бруса длиной dx, ограниченный плоскостями т–т и п–п
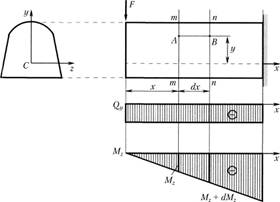
Рис. 2.31
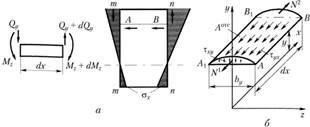
Рис. 2.32
(см. рис. 2.31 и 2.32, а). В нормальном сечении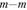
будут действовать напряжения
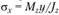, соответствующие осевой силе
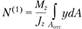, а в нормальном сечении
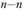– напряжения i
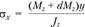, соответствующие осевой силе
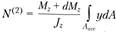. Равнодействующая двух осевых сил
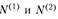равна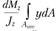
и направлена в сторону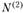
Для выполнения условий равновесия эта равнодействующая должна уравновешиваться касательными силами, действующими на площадке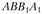
(рис. 2.32, б). Если принять до
пущение о равномерном распределении касательных напряжений по ширине сечения, полагая длину элемента небольшой, можно считать, что касательные напряжения на указанной горизонтальной площадке распределены равномерно и направлены в сторону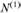
В этом случае уравнение равновесия отсеченного элемента имеет вид
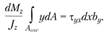
Отсюда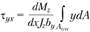
. Поскольку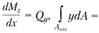
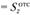и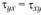 
, получим
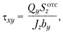(2.76)
где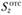 
– статический момент площади отсеченной части сечения относительно оси
; 
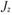– момент инерции сечения; 
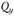– поперечная сила, действующая в данном сечении.
Выражение (2.76), называемое формулой Журавского, устанавливает закон изменения касательных напряжений по высоте поперечного сечения балки.
Для сплошного круглого сечения (рис. 2.33) ввиду симметрии в точках А\ В касательные напряжения равны. Касательное напряжение τ в точке А должно быть направлено по касательной к контуру.
В теории упругости доказано, что касательные напряжения по ширине сечения АВ направлены так, что линии их действия пересекаются в одной точке С. Разложим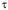
на составляющие 
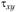и 
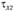. Поскольку 
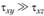, то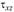 
не учитывают; 
и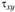 
считают равными и определяют их по формуле Журавского (2.76).
Для длинных балок из конструкционных металлических материалов подбор сечений по условию прочности на изгиб осуществляется по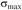
, поскольку роль касательных напряжений незначительна.
Для композитных материалов необходимо после выбора сечения по атах провести проверку прочности по
, поскольку допускаемое напряжение на сдвиг невелико. В этом случае используются два условия прочности:
• для выбора размеров сечения: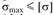
;
• для проверки прочности: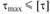
Касательные напряжения в тонкостенных сечениях.
Толщина любого из элементов в тонкостенных сечениях существенно меньше остальных линейных размеров. 'Гонкостенные сечения бывают двух видов: незамкнутого (открытого) профиля и замкнутого. Линия, делящая толщину сечения пополам, называется средней линией. По этой линии строится эпюра касательных напряжений т.
При расчете балок с тонкостенным сечением на прочность определяющую роль играют нормальные напряжения, вычисляемые по формулам (2.73) и (2.74). Однако в отличие от балок со сплошным сечением в данном случае необходимо учитывать величину и закон распределения касательных напряжений.
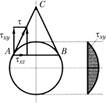
Рис. 2.33
Принимаютсяследующие допущения:
• по толщине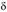
напряжения
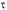распределены равномерно, т.е. одинаковы по величине и направлению;
• направление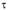
совпадает с направлением касательной к средней линии.
Для тонкостенных сечений, как и для сплошных, формула для τ получается в результате учета равновесия части сечения, но разрез делается плоскостью, нормальной к средней линии, а не параллельной нейтральному слою, как при выводе формулы Журавского.
Внешне формула Журавского (2.76) не изменяет своего вида и для тонкостенных сечений, лишь обозначение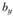
заменяется на 5, однако есть принципиальное отличие: здесь определяются полные напряжения τ, а не
:
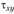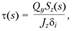(2.77)
где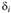 
– толщина /-го участка сечения;
– координата, отсчитываемая вдоль средней линии от начала каждого /-го участка.
Поскольку τ не изменяются по толщине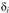
, часто вместо
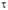используют характеристику
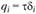, которая называется потоком касательных напряжений (рис. 2.34, а):
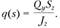
Эту характеристику удобно использовать, еслнб изменяется по контуру; при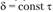
определяют по формуле (2.77).
В каждом сечени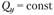и
и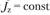
, если же и
,
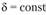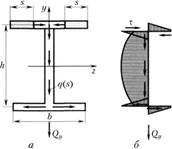
Рис. 2.34
то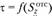
. На рис. 2.34, а показан поток касательных на
пряжений в двутавровом поперечном сечении. Общий вид эпюры касательных напряжений приведен на рис. 2.34, б.
Перемещения при изгибе
Под перемещением балки при изгибе понимается прогиб или угол поворота ее оси. Имеется несколько методов определения перемещений: с помощью дифференциального уравнения упругой линии или по интегралу Мора.
Определение перемещений в балке методом интегрирования дифференциального уравнения упругой линии. Из полученного ранее выражения (2.72) имеем:
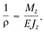
При малых прогибах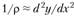
, тогда получим уравнение
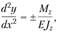(2.78)
которое называется дифференциальным уравнением упругой линии балки.
Выбор знака в этом уравнении определяется направлением координатной оси у. Если она направлена вверх, ставится знак "плюс".
Определим угол поворота и прогиб оси балки, показанной на рис. 2.35, с помощью дифференциального уравнения упругой линии. Подставляя в уравнение (2.78) выражение для изгибающего момента, имеем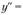 
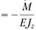. Отсюда 
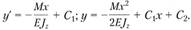. Произвольные постоянные
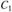и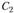
найдем из граничных условий. При
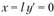, отсюда
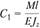. При
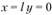, отсюда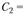
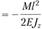
Окончательно получили формулы:
• угла поворота:
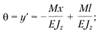(2.79)
Рис. 2.35
• прогиба балки:
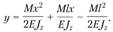(2.80)
Используя зависимости (2.79) и (2.80), можно вычислить прогиб и угол поворота любой точки оси балки, например конца балки:
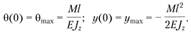
Энергетический метод определения перемещений балок. Для получения расчетных зависимостей рассмотрим потенциальную энергию балки при изгибе.
В пределах упругости потенциальная энергия деформации равна работе внутренних сил на перемещениях точек их приложения. В большинстве случаев в пределах упругости имеет место линейная зависимость между изгибающим моментом и углом поворота нормального сечения, поэтому элементарная работа внутренних сил, равная потенциальной энергии деформации, определяется следующим образом:
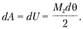(2.81)
Поскольку, уравнение (2.78) можно записать в виде
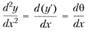
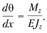
Подставив последнее выражение в равенство (2.81), получим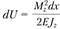 
. Отсюда для потенциальной энергии деформации запишем
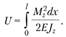(2.82)
Согласно теореме Кастилиано частная производная от потенциальной энергии системы по силе равна перемещению точки приложения силы по направлению ее действия. Таким образом, используя теорему Кастилиано, непосредственно можно вычислить перемещения, ио только тех точек, где приложены внешние силы, и только в направлении этих сил.
Интеграл Мора. На практике часто пользуются интегралом Мора, который получается из рассмотрения баланса энергии. Если имеется несколько (и) участков балки, на которых подынтегральные функции изменяются, берут сумму интегралов, т.е.
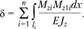(2.83)
Формула (2.83) называется интегралом Мора и служит для определения перемещений балки.
Если необходимо определить не прогиб, а угол поворота сечения, то здесь вместо единичной силы прикладывают единичный момент.
Найдем прогиб конца консоли, показанной на рис. 2.35. Сначала определяем изгибающий момент от внешней нагрузки 
. Затем балка освобождается от внешней нагрузки, и в рассматриваемом сечении А прикладывается единичная сила. Определяется момент от единичной нагрузки: 
Далее вычисляем прогиб:
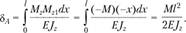
Положительный результат означает, что прогиб направлен вниз, т.е. по заданному направлению единичной силы.