Опционные контракты
Опционный контракт – это договор, предоставляющий покупателю в обмен на премию право продать или купить актив в определенный момент времени в будущем или в течение определенного периода по заранее установленной цене. Одна сторона называется держателем опциона, а другая – продавцом. Опционы на право покупки называют опционами колл (саll), на право продажи – пут (put).
При заключении договора держатель опциона выплачивает продавцу премию, приобретая, таким образом, право исполнения опциона в момент истечения его срока действия или раньше, в зависимости от условий контракта, которые определяются стилем опциона. Принято выделять три стиля опционов: американский, европейский и экзотический.
Американские опционы могут быть исполнены в любой момент времени в течение срока действия, в случае с европейскими исполнение возможно только в момент истечения срока действия. Экзотические опционы имеют более сложную структуру. Среди экзотических наиболее часто встречаются следующие типы опционов: барьерные, опционы с возвратом и азиатские. В барьерных опционах изначально устанавливается цена базисного актива, при преодолении который опцион начинает действовать и может быть исполнен. Цена исполнения опциона с возвратом зависит от минимального или максимального значения, которое принимает цена базисного актива в течение всего срока действия опциона. Расчеты по азиатскому опциону осуществляются на основе разницы между ценой исполнения и средней ценой базисного актива за установленный период, который может совпадать с временем действия опциона. В дальнейшем в данной главе будут рассматриваться в основном европейские опционы.
Существуют как биржевые, так и внебиржевые опционы. По типу базисных активов опционы подразделяются на процентные, валютные, фондовые и товарные. Процентные опционы заключаются на процентные фьючерсы, соглашения о будущей процентной ставке (FRA) или на процентные свопы. Опционы на процентные свопы называют свопционами. Валютные опционы заключаются на валюту или валютные фьючерсы, фондовые – на акции или индексные фьючерсы, товарные – на товары или товарные фьючерсы.
Принципиальным отличием опционов от форвардов, фьючерсов и свопов является то, что они предоставляют держателю право, но не обязательство купить или продать актив по зафиксированной цене. Именно за это право держатель платит опционную премию. Согласно существующей терминологии держатель опциона занимает длинную позицию, которая в зависимости от типа опциона называется "длинный колл" (если это право купить актив) или "длинный пут" (если это право продать актив). Тогда продавец этих опционов будет иметь короткую позицию ("короткий колл" или "короткий пут"), т.е. обязательство продать или купить базисный актив при желании держателя опциона. Представим эти термины в табл. 10.2.
Таблица 10.2. Соотношение видов опционов и позиций
|
Вид опциона |
Позиция |
|
|
короткая |
длинная |
|
|
Колл |
Обязательство продать базисный актив по цене исполнения по требованию держателя опциона |
Право купить базисный актив по цене исполнения |
|
Пут |
Обязательство купить базисный актив по цене исполнения по требованию держателя опциона |
Право продать базисный актив по цене исполнения |
Продавец опциона подвергается существенным рискам, в случае опциона колл возможные убытки по короткой позиции практически неограниченны. Проанализируем возможную прибыль или убыток по приведенным выше четырем опционным позициям.
Для этого введем следующие обозначения:
ST–цена базисного актива на дату истечения опциона T;
X– цена исполнения опциона; с – премия опциона колл; р – премия опциона пут.
Функция выигрыша для держателя европейского опциона "колл" имеет вид: max{ST-X, 0}. Действительно, покупатель может воспользоваться правом приобретения базисного актива по цене X, если его спот-цена окажется выше. Следовательно, выигрыш для длинного опциона колл потенциально неограничен и напрямую зависит от того, насколько вырастет цена на базисный актив, при этом возможный убыток ограничен размером опционной премии с. Симметрично определяется функция выигрыша для продавца опциона колл: – max{ST-X, 0}. Отметим, что короткий опцион колл характеризуется существенной подверженностью риску, поскольку потенциальные убытки продавца в случае роста цены на базисный актив неограниченны. Поэтому для ограничения рисков продавцы зачастую вместе с продажей опциона колл покупают базисный актив. На рис. 10.5, а показан график прибыли (с учетом выигрыша и затрат) для длинного опциона колл, а на рис. 10.5,б – для короткого опциона колл.
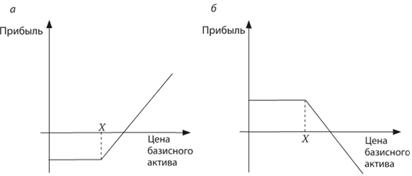
Рис. 10.5. Графики прибыли для длинного (о) и короткого (б) опциона колл
Аналогично выигрыш держателя опциона пут определяется следующей функцией: max{Х – ST, 0}, а для продавца опциона пут – симметрично: –maх{Х – ST, 0}. Графики прибыли для длинного и короткого опциона пут представлены на рис. 10.6, а и 10.6, б соответственно.
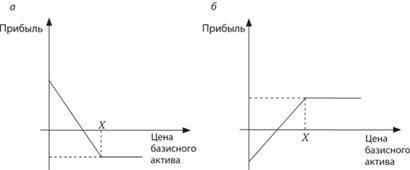
Рис. 10.6. Графики прибыли для длинного (о) и короткого (б) опциона пут
Для держателя опциона пут максимально возможный выигрыш равен цене исполнениях.
Приведем основные свойства американских и европейских опционов.
1. Цена американского опциона больше или равна цене европейского опциона с аналогичными характеристиками. Это утверждение справедливо, поскольку американские опционы расширяют права держателя. Увеличение цены обусловлено возможностью исполнения опциона в любой момент времени в течение срока его действия.
2. Для американских опционов справедливы следующие неравенства:
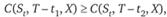 если
если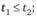
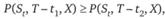 если
если 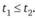
Здесь С и Р – цены американских опционов колл и пут соответственно.
3. Чем больше цена исполнения, тем ниже цена опциона колл. Чем больше цена исполнения, тем выше цена опциона пут. Это свойство следует из вида платежной функции опционов колл и пут и связано с возможностями исполнить опцион. Свойство справедливо как для европейских, так и для американских опционов.
4. Цена опциона колл является выпуклой функцией от цены базисного актива. Поясним данное свойство. Рассмотрим два опциона колл с ценами исполнения X1 и Х2. При этом цена третьего опциона является выпуклой комбинацией: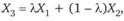 где
где 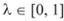 . Тогда для цены третьего опциона справедливо следующее неравенство:
. Тогда для цены третьего опциона справедливо следующее неравенство:
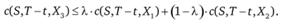
Паритет цен европейских опционов. На совершенном рынке цены европейских опционов колл и пут связаны между собой следующим соотношением:
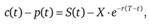
где с(t) – цена опциона колл в момент времени t; p(t) – цена опциона пут в момент времени t; r – безрисковая процентная ставка на срок (Т-t) лет при непрерывном начислении процентов.
Докажем формально это равенство. Рассмотрим два портфеля. Один состоит из опциона пут и единицы базисного актива, а второй – из опциона колл и суммы 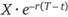 , инвестированной на период [t; Т] под безрисковую процентную ставку г. Следовательно, текущая стоимость первого портфеля составляет
, инвестированной на период [t; Т] под безрисковую процентную ставку г. Следовательно, текущая стоимость первого портфеля составляет 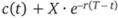 , а второго – p(t) + S(t). В момент истечения опциона стоимость первого портфеля окажется равной
, а второго – p(t) + S(t). В момент истечения опциона стоимость первого портфеля окажется равной
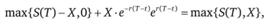
а второго – 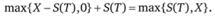
Таким образом, инвестирование средств в оба портфеля приводит к одинаковому результату. Это означает, что и текущие стоимости портфелей должны совпадать, т.е. 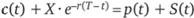 . Перегруппировав слагаемые, получаем равенство, которое требовалось доказать.
. Перегруппировав слагаемые, получаем равенство, которое требовалось доказать.
Если паритет цен не выполняется, это означает, что на рынке имеются арбитражные возможности, которые, как правило, быстро ликвидируются. Если за время, оставшееся до истечения опциона, по базисному активу поступают доходы, то паритет цен записывается следующим образом:
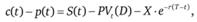
где PVt(D) –дисконтированная стоимость доходов, поступающих по базисному активу за период [t; Т].
Опционные стратегии. Существует много различных комбинаций опционов и базисных активов. Эти комбинации классифицируют по уровню риска и выигрыша, по характеру ожиданий ("бычьи", "медвежьи", нейтральные), по входящим позициям (только различные опционы или опционы с базисными активами), по целям (спекулятивные, хеджирующие) и т.д. Рассмотрим наиболее простые стратегии торговли опционами.
Стратегия покрытого опциона колл (covered call) состоит в покупке базисного актива и одновременной продаже опциона колл на этот актив. В этом случае при увеличении цен на базисный актив инвестору не придется покупать его для исполнения обязательства по опциону. График прибыли для покрытого опциона колл представлен на рис. 10.7, а. В этом случае максимальный риск и выигрыш ограничены.
Защитная стратегия покупки опциона пут (protective put) состоит в одновременной покупке базисного актива и опциона пут на данный актив. Таким образом, инвестор защищает свою позицию от падения цен, так как в этом случае будет увеличиваться стоимость опциона пут. График прибыли от этой стратегии представлен на рисунке 10.7, б.
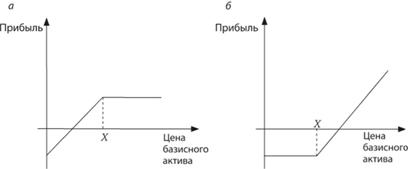
Рис. 10.7. Графики прибыли для покрытого опциона колл (а) и защитного опциона пут (б)
Стратегия "стрэддл" (straddle) состоит из разных позиций по опционам колл и пут с одинаковыми ценами исполнения и датами истечения. Стратегия "стрэнгл" (strangle) состоит из опционов с разными ценами исполнения.
Стратегии, состоящие в комбинировании опционов одного вида, называют спредами. Спред "быков" состоит из короткой позиции по опциону колл (пут) и длинной по опциону колл (пут) с одной и той же датой истечения, но с разными ценами исполнения, причем цена исполнения по короткой позиции должна быть выше, чем по длинной. Такой спред применяется, если инвестор полагает, что цены на базисные активы повысятся. График выигрыша для "бычьего" спреда изображен на рис. 10.8, а.
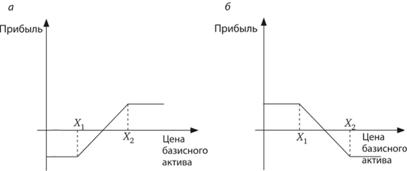
Рис. 10.8. Графики выигрыша для "бычьего" (о) и "медвежьего" (б) спреда
Аналогичная стратегия, применяемая при игре на понижение, называется спредом "медведей", состоящим из короткой позиции по опциону колл (пут) и длинной позиции по опциону колл (пут) с одной и той же датой истечения, но с разными ценами исполнения, причем цена исполнения по длинной позиции должна быть выше, чем по короткой. График выигрыша для "медвежьего" спреда изображен на рис. 10.8, б.
Существуют и более сложные спреды, состоящие более чем из двух позиций. Примерами таких стратегий являются спред "бабочка" и спред "сэндвич".
Спред "бабочка" состоит из длинной позиции по двум опционам колл с ценами исполнения Х1 и Х3 и короткой позиции по двум опционам колл с ценой исполнения 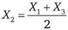 . Затраты на создания такого спреда составят с1 + с3 – 2с2. Данное выражение является положительным в силу выпуклости платежной функции опциона колл относительно цены исполнения. В момент истечения опционов выигрыш составит
. Затраты на создания такого спреда составят с1 + с3 – 2с2. Данное выражение является положительным в силу выпуклости платежной функции опциона колл относительно цены исполнения. В момент истечения опционов выигрыш составит
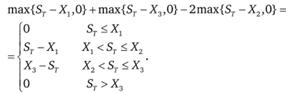
Функция прибыли (с учетом затрат и выигрыша) построена на рис. 10.9.
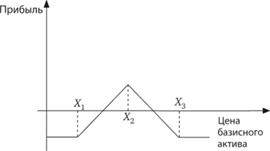
Рис. 10.9. Функция прибыли от спреда "бабочка" (с учетом затрат и выигрыша)
Из графического представления прибыли от реализации данной стратегии очевидно, чем обусловлено название спреда.
По сути, данный спред является комбинацией спреда "быков" и спреда "медведей". Такая стратегия используется в том случае, если инвестор полагает, что резкие изменения цены базисного актива маловероятны.
Оценка опционов. Опционную премию условно можно разделить на две части: внутренняя стоимость и временна́я стоимость. Внутренняя стоимость представляет собой разность между ценой базисного актива и ценой исполнения, а временна́я стоимость – между премией и внутренней стоимостью. По сути, внутренняя стоимость отражает выигрыш по опциону, который ожидается на данный момент. Временна́я стоимость – функция, обратно зависящая от времени, остающегося до истечения опциона. Временна́я стоимость отражает возможности того, что выигрыш по опциону увеличится благодаря изменению конъюнктуры на спот-рынке. По этой причине в момент исполнения опциона временна́я стоимость равна нулю и цена совпадает с внутренней стоимостью.
Существует классификация опционов в зависимости от соотношения цены исполнения и спот-цены базисного актива. Если цена исполнения равна цене базисного актива, то говорят, что опцион без выигрыша (at-the-money). В этом случае премия по опциону совпадает с его временной стоимостью. Если выигрыш по опциону положителен, т.е. его исполнение приносит прибыль, то его называют опционом с выигрышем (in-the-money). В обратном случае это опцион с проигрышем (out-of-the-money).
Очевидно, что вопрос оценки стоимости опциона является достаточно сложным, так как его временна́я стоимость зависит от множества факторов, таких, как конъюнктура на рынке базисных активов, время до истечения опциона, безрисковая доходность и т.д. По этой причине было предложено множество моделей, в основе которых лежат различные предположения о поведении цен базисных активов. Наибольшую известность получила модель, которая была построена Фишером Блэком и Майроном Шоулзом. В основе модели Блэка-Шоулза лежат следующие допущения:
1) рынки являются совершенными;
2) цены на базисные активы изменяются непрерывно;
3) процентные ставки известны и постоянны;
4) волатильность базисных активов постоянна.
Для построения модели оценки опционов используется теория случайных процессов, включая теорию стохастических дифференциальных уравнений в частных производных. Приведем основные этапы вывода уравнения Блэка – Шоулза. В основе модели лежит предположение о том, что поведение цен на спот-рынке в течение срока жизни опциона является случайным процессом, который может быть описан геометрическим броуновским движением. Это означает, что на бесконечно малом интервале времени dt логарифмическая доходность распределена нормально с математическим ожиданием mdt и дисперсией σ2dt. Формально геометрическое броуновское движение цен базисных активов может быть записано с помощью следующего стохастического дифференциального уравнения: dSt = (mSt)dt + (σSt)dwt, где wt – винеровский случайный процесс. Таким образом, в центре нашего внимания находится цена опциона, представляющая собой функцию от случайного процесса и от времени, оставшегося до истечения опциона. Обозначим цену опциона колл c(St, t). Блэк и Шоулз показали, что в предположениях о совершенном рынке на основе динамической хеджирующей стратегии можно сформировать безрисковый портфель, состоящий из опциона колл и базисного актива, объем которого непрерывно меняется. Обозначим его через Дг. Тогда стоимость данного портфеля равна: V(t) = – c(St, t) + ΔtSt. Проанализируем изменения стоимости безрискового портфеля во времени. Для этого найдем дифференциал стоимости портфеля: dV=-dc(St, t) + ΔtdSt. Учитывая, что St представляет собой геометрическое броуновское движение, по лемме Ито дифференциал функции c(St, t) от случайного процесса Ито равен:
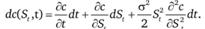
Тогда
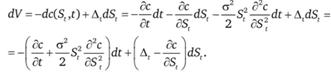
Подставив уравнение для геометрического броуновского движения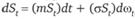 , получим
, получим
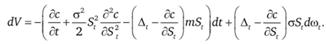
Отсюда найдем кумулятивную стоимость портфеля за период т, проинтегрировав полученное выражение от 0 до τ:
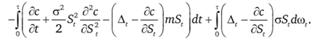
Заметим, что стохастическим в этом выражении является только последнее слагаемое: 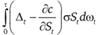 , так как wt – винеровский случайный процесс. Предположим, что инвестор применяет динамическую хеджирующую стратегию, состоящую в том, что количество базисного актива непрерывно меняется во времени в соответствии со следующей формулой:
, так как wt – винеровский случайный процесс. Предположим, что инвестор применяет динамическую хеджирующую стратегию, состоящую в том, что количество базисного актива непрерывно меняется во времени в соответствии со следующей формулой: 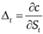 для t < τ. Тогда рассматриваемое слагаемое будет равно нулю, и кумулятивная стоимость портфеля окажется детерминированной величиной. Очевидно, что при отсутствии арбитражных возможностей стоимость рассматриваемого портфеля должна совпадать со стоимостью безрискового актива, в который инвестирована сумма:
для t < τ. Тогда рассматриваемое слагаемое будет равно нулю, и кумулятивная стоимость портфеля окажется детерминированной величиной. Очевидно, что при отсутствии арбитражных возможностей стоимость рассматриваемого портфеля должна совпадать со стоимостью безрискового актива, в который инвестирована сумма: 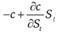 . Доход от инвестирования данной суммы под безрисковую процентную ставку r составит
. Доход от инвестирования данной суммы под безрисковую процентную ставку r составит
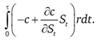
Поскольку при отсутствии арбитражных возможностей доходы от эквивалентных альтернатив должны совпадать, приравняем
выражения, полученные для захеджированного портфеля и актива, инвестированного под безрисковую процентную ставку:
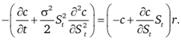
Отсюда для любой цены базисного актива S получим
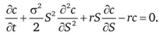
Данное дифференциальное уравнение в частных производных называется уравнением Блэка – Шоулза. Начальным условием, позволяющим получить частное решение данного уравнения, является выигрыш от опциона в момент исполнения:
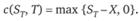
Из полученной модели очевидно, что цена опциона зависит от следующих параметров:
1) спот-цены актива S;
2) момента исполнения опциона Т;
3) цены исполнения X;
4) безрисковой процентной ставки r;
5) волатильности базисного актива σ.
Заметим, что цена опциона не зависит от математического ожидания доходности актива т. Это объясняется предположением о нейтральном отношении инвестора к риску. В реальности, за больший риск инвестор, как правило, требует большей ожидаемой доходности. Одним из объяснений правомерности предположения о нейтральном отношении к риску является предположение о возможности построения идеального динамического хеджа. По этой причине в модели возможно считать, что доходность актива совпадает с безрисковой доходностью. В то же время следует заметить, что доходность базисного актива влияет на его текущую цену, оказывая, таким образом, косвенное влияние на цену опциона.
Результатом решения дифференциального уравнения Блэка – Шоулза в частных производных с соответствующим начальным условием является следующее выражение для цены опциона:
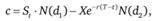
где с – цена (премия) опциона колл; St – цена базисного актива в текущий момент времени t; X – цена исполнения опциона; Т – дата истечения опциона; r – безрисковая процентная ставка; N(d) – значение стандартной нормальной функции распределения в точке d, т.е. 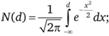
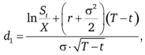
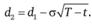
Аналогичным образом может быть получена формула для оценки опциона пут. Кроме того, ее можно получить исходя из паритета цен европейских опционов:
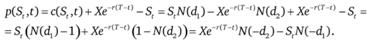
Проверим, удовлетворяет ли полученная формула экономическим представлениям о поведении цены опциона при экстремальном изменении цены базисного актива. Легко видеть, что при St → 0 d1→-∞, следовательно, N(-d1) → 1, a StN(-d1) → 0. Таким образом, при 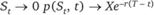 . Действительно, это максимальная выгода, которая может быть получена. Если же цена актива St → ∞, то не имеет смысла исполнять опцион, а значит, выгода от
. Действительно, это максимальная выгода, которая может быть получена. Если же цена актива St → ∞, то не имеет смысла исполнять опцион, а значит, выгода от 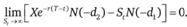 него должна быть равна нулю. Действительно
него должна быть равна нулю. Действительно