Общая схема оценивания прогнозных моделей z-множителями

Мы уже обращали внимание на одну очевидную мысль: МНК является лишь одним из возможных и далеко не самым лучшим методом оценки коэффициентов моделей прогнозирования процессов социально-экономической динамики. Даже в случае применения выборочного подхода обратимых процессов МНК является лучшим способом оценки коэффициентов модели лишь в ситуации нормального распределения случайных величии. Для других распределений предпочтительными будут другие методы – обобщенный метод моментов, метод максимального правдоподобия, метод Ньютона, метод спейсингов или разнообразные методы непараметрической регрессии. Конечно, МПК используется чаще всего при обработке статистических выборок, но это вовсе не говорит о том, что он – лучший метод для любых ситуаций. Просто чаще всего в случайных совокупностях проявляются условия, для которых наилучшим будет именно МНК – множество случайных факторов действуют на статистический показатель незначительно, причем действуют разнонаправлено, поэтому результат этого действия вполне описывается нормальным распределением.

Какие же методы могут выступить в виде альтернативы МНК для решения задачи оценивания коэффициентов моделей, описывающих необратимые процессы? Ведь эти процессы многообразны и узнать наперед, к какому типу они относятся, чтобы применить лучший метод (или набор методов), чаще всего нельзя. Нужен некоторый набор различных методов, в том числе и МПК, для того, чтобы, испробовав каждый из них, с помощью процедуры ретропрогноза выбрать лучший для процесса метод. Вместо априорного подхода, характерного для задач математической статистики, следует использовать апостериорный подход, когда тщательно изучив особенности прогнозируемого процесса, нс задавая никаких предварительных предположений о нем, испробовав несколько подходов и методов оценки прогнозной модели, выбирают наилучший из них.

При построении прогнозных моделей необратимых процессов прогнозист не может быть уверен в том, какая модель лучше всего будет прогнозировать следующие будущие наблюдения – та, которая имеет в прошлом минимальную дисперсию, та, которая имеет в прошлом нормально распределенные остатки, или какая-то еще. Для такого априорного вывода нет никаких оснований. Необходимо различными методами сгенерировать множество различных оценок выбранной модели на некоторой части имеющейся базы; проверить с помощью процедуры ретропрогноза точность прогноза каждого из методов оценки коэффициентов модели на проверочном множестве и отдать предпочтение тому из них, который показал наилучшие прогнозные оценки. Здесь, конечно, мы возвращаемся к индуктивному методу, предполагая, что если некоторый выбранный метод в прошлом давал лучшие прогнозные оценки, то и в будущем он будет обладать подобными же свойствами. Но так и делается в современной науке – она представляет собой синтез гипотетико-эмпирического и эмпирико-дедуктивного выводов.

Покажем, как можно получить множество способов оценивания коэффициентов прогнозных моделей с помощью метода z-множителей^[1].

Следуя общенаучному принципу "от простого – к сложному", рассмотрим самую простую модель линейной однофакторной зависимости, на примере которой будет ясен смысл метода 2-множителей. После этого можно будет легко использовать метод и для оценки коэффициентов более сложных моделей.

Вспомним вначале, что для нахождения значений коэффициентов прогнозной модели мы должны каким-то образом получить такое число уравнений k, которое бы соответствовало числу k неизвестных коэффициентов этой модели. Решая эту систему из k уравнений с k неизвестными, можно найти численные значения коэффициентов.

Действительно, если, например, перед прогнозистом стоит задача найти коэффициенты линейного тренда (с двумя коэффициентами), то тот же МНК предлагает ему решить систему двух нормальных уравнений с двумя неизвестными, в результате чего вычисляются значения двух неизвестных коэффициентов тренда. Если же прогнозисту необходимо оценить значения коэффициентов квадратичной функции с тремя коэффициентами, тот же МНК приводит его к необходимости решения системы трех нормальных уравнений и т.д. Следовательно, необходимо, каким-то образом обрабатывая статистические данные, получить систему из такого количества независимых уравнений, сколько неизвестных коэффициентов содержит прогнозная модель.

Любая модель, очевидно, описывает реальный процесс с некоторой ошибкой аппроксимации εt, поэтому для любого значения t выполняется такое равенство:

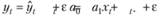(10.22)

Для использования этой модели при прогнозировании необходимо на имеющемся множестве значений yt найти значения двух коэффициентов – а0 и а1. Значит, надо каким-то образом построить два уравнения с этими двумя неизвестными коэффициентами и, решая эту систему из двух уравнений, оценить значения коэффициентов прогнозной модели.

Очевидно, что равенство (10.22) не нарушится, если его левую и правую части умножить на некоторый заранее известный заданный прогнозистом множитель :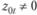

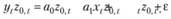(10.23)

Если теперь просуммировать левую и правую части полученного равенства по всем наблюдениям t, получим уравнение

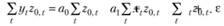(10.24)

Теперь умножим левую и правую части равенства (10.22) на другой, также заранее известный и заданный прогнозистом множитель 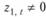, не являющийся линейным преобразованием множителя :

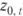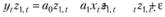(10.25)

Просуммировав теперь и это уравнение по всем наблюдениям ί, получим второе уравнение:

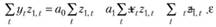(10.26)

Сведем уравнения (10.23) и (10.26) в одну систему:

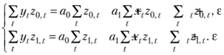(10.27)

Данная система – система двух линейных уравнений с (Т + 2) неизвестными – а0, а1 и εt (численные значения множителей z0,t и z1,t задаются прогнозистом). Очевидно, что эта система имеет множество возможных решений, и потому для задачи нахождения оценок коэффициентов линейной однофакторной модели она непригодна. Но на ее основе можно добиться решения поставленной задачи, для чего необходимо задать некоторые дополнительные условия к этой системе.

Для задания этих условий будем исходить из того очевидного положения, что точность описания некоторого процесса с помощью любой модели определяется характером ошибок аппроксимации εt. Поэтому, если и следует задавать некоторые условия к задаче (10.27), то их следует связывать именно с этими ошибками аппроксимации. Можно, например, задать такие дополнительные условия именно относительно этих ошибок аппроксимации:

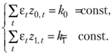(10.28)

где k0 и k1 – наперед заданные числа.

Тогда при выполнении условий (10.28) система уравнений (10.27) будет записана так:

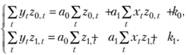
Поскольку k0 и k1 заданы, то получена система двух уравнений с двумя неизвестными, которое имеет одно решение. Очевидно, что значения коэффициентов модели будут определяться как характером задания 2-множителей, так и значениями констант k0 и k1.

Самый простой случай рассматриваемой задачи соответствует ситуации, когда k0 = k1 = 0, т.е.

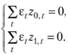(10.29)

Для него будет получена система

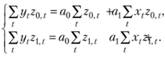(10.30)

С ее помощью коэффициенты а0 и а1 могут быть легко найдены.

Такой случай предпочтительнее случая, задаваемого условием (10.28), поскольку при этом появляется возможность интерпретации свойств получаемых оценок.

Действительно, пусть, например, используются такие 2-множители:

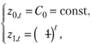(10.31)

а относительно ошибок аппроксимации выполняется (10.29). Тогда в случае, если число наблюдений Г четное, получим

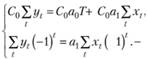(10.32)

Коэффициенты прогнозной модели для этого способа находятся очень просто – из второго уравнения сразу же вычисляются значения коэффициента а1, а после этого, подставляя полученные значения в первое уравнение системы, легко найти а0. Следует отметить, что для этой модели выполняются условия

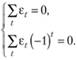(10.33)

которые со всей очевидностью следуют из (10.29).

Из этой системы равенств вытекает понимание того, что будет собой представлять линейная модель, если использовать этот способ задания 2-множителей.

Так, сумма отклонений расчетных значений модели от фактических всегда будет равна нулю. Это означает, что модель с коэффициентами, полученными таким способом задания 2-множителей, будет всегда проходить через среднюю арифметическую точку. Это со всей очевидностью следует из первого равенства системы (10.32).

Второе равенство (10.33) свидетельствует о том, что сумма ряда ошибок аппроксимации εt, умноженных на знакочередующийся ряд единиц, будет равна нулю (второе равенство системы (10.33)). В результате этого второе равенство системы (10.32) может быть записано так: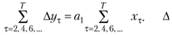

Это значит, что коэффициент пропорциональности находится через приросты показателей и характеризует средний прирост за рассматриваемый период.

Итак, во-первых, с помощью системы (10.30), задавая различные значения 2-множителей, можно получить и различные значения коэффициентов прогнозной модели. Во-вторых, с учетом одновременного выполнения системы равенств (10.29) и (10.30) прогнозист имеет дополнительную информацию о том, какими свойствами обладают ошибка аппроксимации и применяемый метод оценки коэффициентов прогнозной модели. Заметим, однако, что построение модели по выборке с учетом условия (10.29) еще не гарантирует, что и на периоде прогнозирования это условие будет выполняться. Однако если в исследуемом ряде данных не будет происходить существенных качественных изменений, можно по индукции ожидать выполнения условия (10.29) в будущем.

Сразу же возникает вопрос: а как соотносится этот метод с методом наименьших квадратов? Ответ прост: если множители задать так:

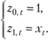(10.34)

то, подставляя их в (10.30), получим систему двух уравнений, которая в точности будет соответствовать системе нормальных уравнений МНК. Действительно, в этом случае получим

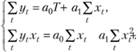(10.35)

Но теперь метод 2-множителей позволяет получить не только оценки МНК применительно к линейной модели, но и дополнительную интерпретацию оценок МНК, поскольку будет выполняться и условие (10.29). Мы можем с полным основанием утверждать, что МНК, примененный к линейной функции, дает такие значения коэффициентов модели, при которых всегда выполняются условия

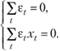(10.36)

Какой смысл имеют эти условия?

Первое равенство в системе (10.36) свидетельствует о том, что для оценок МНК сумма ошибок аппроксимации всегда будет равна нулю и всегда оценки МНК линейной однофакторной зависимости будут такими, что модель будет проходить через среднюю арифметическую наблюдений. А если описываемый с помощью линейной модели процесс будет нелинейным, как будет вести себя модель, коэффициенты которой найдены с помощью МНК? Как следует из первого равенства (10.36), модель пройдет через среднюю точку, а сумма отклонений фактических значений от расчетных будет равна нулю. Иногда приходится сталкиваться с экономистами, которые считают, что если для построенной с помощью МНК модели сумма ошибок аппроксимации равна нулю, то модель лучше всего описывает исследуемый процесс. Ошибочность этой точки зрения теперь очевидна – МНК, примененный к любому процессу, будет всегда давать такие оценки коэффициентов модели (неважно, линейной или нелинейной), при которых сумма ошибок аппроксимации равна нулю. О пригодности или непригодности модели сумма ошибок аппроксимации ничего не говорит.

Чтобы понять смысл второго равенство в системе (10.36), нужно обратиться к ковариации между ошибкой и фактором хt.

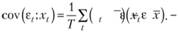(10.37)

Средняя величина по ошибкам в связи с первым равенством в (10.36) будет равна нулю, поэтому ковариация в (10.37) упростится до вида

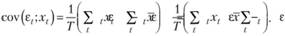(10.38)

В (10.38) в правой части полученного равенства второе слагаемое в скобках представляет собой произведение средней арифметической на сумму ошибок, которая в силу того же равенства (10.36) будет равна нулю. В результате получаем равенство, включающее в себя второе равенство из (10.36):

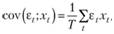
Таким образом, второе условие в (10.36) гарантирует получение таких оценок коэффициентов, при которых ковариация между ошибками и фактором xt всегда будет равна нулю, что фактически влечет за собой условие некоррелированности ошибок с регрессорами в уравнении, оцененном МНК. Это указывает на то, что в случае корректной оценки модели методом наименьших квадратов в модели не может быть проблемы эндогенности.

Как видно, МНК является частным случаем Общей схемы оценивания (ОСО) коэффициентов модели с помощью 2-множителей. Задавая различные 2-множители, прогнозист,

решая систему (10.30), получает различные значения коэффициентов линейной однофакторной модели и выбирает ту пару значений 2-множителей, при которой ошибка ретропрогноза минимальна. Это могут быть и оценки МНК, но для необратимых процессов чаще всего это будут другие оценки.

Кроме того, исследователь может оценить коэффициенты модели (10.22) таким образом, чтобы выполнялись нужные ему предположения. В качестве варианта таких предположений можно предложить отсутствие автокорреляции первого порядка, что в случае, если сумма ошибок равна нулю, записывается как

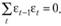
Осуществляется это путем задания z-множителей в виде

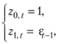
откуда следует такая система уравнений:

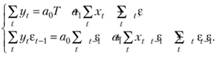(10.39)

Примем выполнение таких условий:

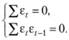
Полученная система в итоге упрощается до

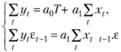(10.40)

Однако для осуществления расчетов по (10.40) исследователю нужно предварительно иметь ошибки εt-1 которые послушаются лишь после оценки модели. Данная задача может быть решена итеративно: оценив модель, например, с помощью МНК, получают первоначальный набор ошибок, который затем используется в переоценке модели в соответствии с условиями (10.40).

Как видим, метод 2-множителей позволяет задавать различные условия при построении модели, которые могут быть нужны в различных ситуациях.

Рассмотрим теперь, как можно использовать метод 2-множителей для более сложных моделей, например квадатичной модели:

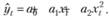(10.41)

Поскольку модель содержит три неизвестных коэффициента а0, а1 и а2, то необходимо использовать три множителя: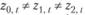(не являющихся линейным преобразованием друг друга) для получения системы из трех уравнений с тремя неизвестными. Опуская вывод системы уравнений метода 2-множителя, аналогичный выводу системы уравнений для линейной однофакторной модели, получим следующую систему для нахождения значений коэффициентов квадратичной модели (10.41):

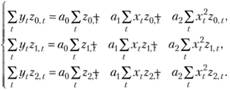(10.42)

которой соответствует система равенств, задающая условия для ошибки аппроксимации:

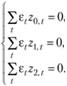(10.43)

Покажем, как получить из этой общей системы оценивания коэффициентов квадратичной модели такие коэффициенты, которые будут соответствовать оценкам МНК. Для этого зададим такие множители: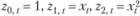

Тогда система (10.42) будет соответствовать системе нормальных уравнений МНК. Действительно, подставляя эти множители в (10.42), получим

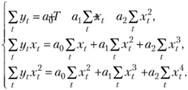(10.44)

что, как легко убедиться, полностью соответствует системе уравнений МНК.

Если теперь задать, например, совокупность множителей 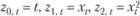, то полученные оценки будут близки к оценкам МНК, но все же отличаться от них.

Изложенный метод 2-множителей позволяет предложить бесконечное множество способов оценки коэффициентов моделей прогнозирования, причем МНК – только один из этого множества. Поэтому, используя разумное число возможных комбинаций и способов задания множителей, прогнозист может из этого множества выбрать тот из них, который демонстрирует свои лучшие свойства в процедуре ретропрогноза.

Методическое свойство метода 2-множителей заключается в том, что с его помощью можно легко сформулировать систему нормальных уравнений МНК для любых аддитивных моделей, что позволяет сформировать систему нормальных уравнений для различных моделей, не прибегая к утомительному выводу этой системы традиционным путем через вычисление производных по коэффициентам функции минимизации суммы квадратов отклонений фактических значений от расчетных.

Пусть, например, прогнозист хочет с помощью МНК оцепить коэффициенты такой модели:

Для построения системы нормальных уравнений МПК оценивания коэффициентов этой модели с помощью ОСО следует левую и правые части равенства умножить на 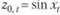, после чего просуммировать по всем t. После этого левую и правую части равенства следует вновь умножить на 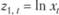, после чего полученные произведения просуммировать по всем t. Сведем два полученных уравнения в систему:

Не менее просто получить систему нормальных уравнений МНК для многофакторной аддитивной модели, например, такой:

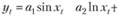(10.45)

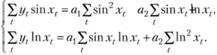(10.46)

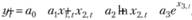(10.47)

Z-множители такой модели для получения системы нормальных уравнений очевидны:

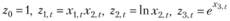(10.48)

С их помощью легко получить искомую систему уравнений:

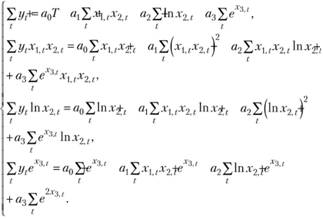(10.49)

Естественно, что в силу (10.29) для полученных оценок МНК будут выполняться следующие условия:

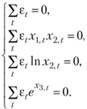(10.50)

Теперь, как видно, можно сформировать систему нормальных уравнений для оценки с помощью МНК коэффициентов любой аддитивной модели.

Эта методическая помощь важна, но в рассматриваемом контексте не является самоцелью. Для эволюционных процессов оценки МНК не являются наилучшими, поэтому, используя различные 2-множители, можно получать самые различные системы уравнений, в результате решения которых формируется семейство оценок коэффициентов, из которого посредством процедуры ретронрогноза выбирается лучший набор 2-множителей.

Метод 2-множителей может быть так же легко представлен в матричном виде. Модель множественной линейной регрессии в матричном виде записывается следующим образом:

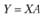, (10.51)

где

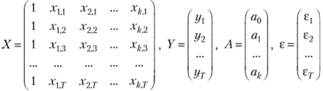
Сформируем матрицу, состоящую из 2-множителей:

Умножение матрицы Z на все элементы уравнения (10.51) даст нам следующее равенство:

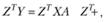(10.52)

естественным предположением в котором будет:

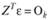, (10.53)

где Оk – вектор-столбец длиной к, составленный из нулей.

Условие (10.53) как раз гарантирует то, что произведение всех 2-множителей на ошибки будет равно нулю. С учетом этого итоговая формула для получения оценок коэффициентов в (10.51) будет иметь вид

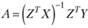(10.54)

В эконометрике схожим образом вычисляются оценки коэффициентов в случае с применением метода инструментальных переменных. Метод z-множителей от метода инструментальных переменных отличают три особенности:

1. В качестве z-множителей могут выступать любые переменные по выбору исследователя, вне зависимости от предположений относительно эндогенности переменных в модели.

2. Из метода z-множителей явно следует условие (10.53), которое является определяющим при принятии решения о том, какую модель исследователь хочет получить, т.е. принцип метода z-множителей отличается от принципа метода инструментальных переменных: исследователь задает условия, в которых хочет построить модель, после чего составляет соответствующую матрицу z-множителей и оценивает коэффициенты модели.

3. Метод инструментальных переменных позволяет оценивать коэффициенты регрессий в случае, если в качестве инструментов выбрано такое количество переменных, которое оказывается не меньше коэффициентов в модели (с учетом константы). В случае с методом z-множителей число z-множителей должно совпадать с числом столбцов в матрице X, иначе ограничения на ошибки не имеют смысла, т.е. в методе z-множителей требования к количеству множителей более жесткие.

Из второго условия, в частности, следует, что какие бы переменные исследователь ни включил в матрицу Z, они не будут коррелировать с ошибками в модели. Однако если в качестве z-множителей выбирать переменные, не входящие в регрессию, то для переменных X, включенных в нее, условие некоррелированности с ошибкой перестает действовать, т.е. в случае использования инструментальных переменных исследователь может получить модель с обозначенной выше проблемой эндогенности. При этом проблема становится менее явной, если выбранные z-множители сильно коррелируют с факторами модели X. Поэтому использование инструментальных переменных само по себе сопряжено с некоторыми рисками, о которых прогнозист должен знать.

Формально же расчеты по данным двум методам в случае равенства числа инструментальных переменных числу коэффициентов в модели осуществляются одинаково, по формуле (10.54).

Рассмотрим простой пример. В табл. 10.2 приведены статистические данные, которые мы будем использовать для демонстрации метода 2-множителей.

Таблица 10.2

Данные условного примера

Месяц	Объем продаж, y	Доход потребителей, х1	Затраты на рекламу, х2	Рыночная цена продукции, х3
Январь 2009 г.	149	10 078,82	11 000	127
Февраль 2009 г.	153	9901,76	10 000	105
Март 2009 г.	277	9968,59	11 000	157
Апрель 2009 г.	163	11 827,17	11 000	136
Май 2009 г.	153	11 496,26	10 000	127
Июнь 2009 г.	248	11 954,79	10 000	136
Июль 2009 г.	253	12 012,63	10 000	142
Август 2009 г.	267	11 672,39	11 000	152
Сентябрь 2009 г.	273	11 719,17	11 000	153
Октябрь 2009 г.	167	13 167,83	11 000	134
Ноябрь 2009 г.	274	13 308,06	11 000	143
Декабрь 2009 г.	175	13 200,16	11,000	142
Январь 2010 г.	172	13 286,91	11 000	144
Февраль 2010 г.	182	13 149,22	12 000	129
Март 2010 г.	201	13 504,04	13 000	164
Апрель 2010 г.	375	13 152,63	14 000	196
Май 2010 г.	205	13 398,53	14 000	171
Июнь 2010 г.	371	13 635,36	13 000	198
Июль 2010 г.	362	14 521,33	14 000	199
Август 2010 г.	350	14 497,11	13 000	186
Сентябрь 2010 г.	192	14 855,05	12 000	163
Октябрь 2010 г.	194	14 784,21	13 000	109
Ноябрь 2010 г.	365	14 633,45	14 000	198
Декабрь 2010 г.	403	14 476,58	15 000	210
Январь 2011 г.	235	14 485,14	15 000	210
Февраль 2011 г.	449	14 582,06	16 000	243
Март 2011 г.	434	14 658,35	15 000	234
Апрель 2011 г.	475	14 523,20	16 000	254
Май 2011 г.	238	14 550,53	15 000	199
Июнь 2011 г.	236	14 568,49	15 000	192
Июль 2011 г.	446	15 742,71	16 000	233
Август 2011 г.	461	15 522,71	15 000	245
Сентябрь 2011 г.	249	15 461,62	16 000	233

На статистических данных с января 2009 г. по декабрь 2010 г. мы будем с помощью разных способов задания z-множителей оценивать коэффициенты многофакторной линейной модели. Данные за 2011 г. мы используем как проверочные для определения точности ретропрогноза. Будем использовать три способа задания множителей:

1. 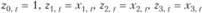, который подразумевает выполнение условий МНК:

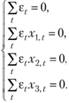(10.55)

2. 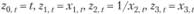, в соответствии с которым выполняется

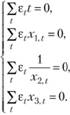(10.56)

3. :

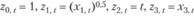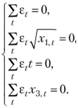(10.57)

Первый способ задания 2-множителей, очевидно, соответствует оценкам МНК. Второй способ будет приводить к тому, что прогнозная модель будет построена со смещением (что следует из условия (10.56)), в связи с тем, что мы убрали условие равенства суммы ошибок нулю. Из-за этого и произведение ошибок на z-множители уже не соответствует корреляции между этими компонентами. Из условия (10.57) следует, что корреляция между ошибкой и х1 и ошибкой х2 может быть отлична от нуля. Однако это позволяет нам наложить другие условия: некоррелированности ошибок со временем и с корнем из х1. Использование таких 2-множителей позволило построить следующие модели (табл. 10.3).

Таблица 103

Модели, построенные на основе данных табл. 10.2 с помощью метода 2-множителей

Модель	Уравнение модели	sMAPE по ряду, %	sMAPE по прогнозу, %
(10.35)		16,32	20,54
(10.36)		38,38	15,19
(10.37)		15,91	22,72

Как видим, модели существенно различаются по значениям коэффициентов. Кроме того, ошибки аппроксимации у них так же различаются: наименьшая ошибка аппроксимации оказалась в модели (10.57), наивысшая – в (10.56). Модель, рассчитанная МНК, оказалась достаточно точной в аппроксимации и по ошибке ближе к последней модели. При этом точность прогноза оказалась выше у модели (10.56), нежели у других моделей.

Графически аппроксимация исходного ряда и прогнозы по моделям представлены на рис. 10.5.

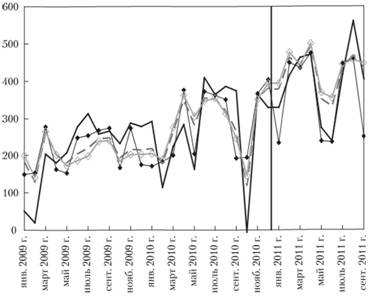
Рис. 10.5. Условный ряд данных (сплошная линия с закрашенными точками), его аппроксимация и прогнозы по моделям (10.55) (пунктирная линия), (10.56) (сплошная линия) и (10.57) (сплошная линия с незакрашенными точками):

слева от вертикальной линии – значения, по которым осуществлялась аппроксимация; справа – прогноз

Заметно, что модель (10.56), построенная с систематической ошибкой, аппроксимирует исходный ряд данных хуже всех (а в октябре расчетное значение по модели и вовсе оказалось отрицательным), однако она же оказывается и самой точной на периоде ретропрогноза за счет того, что более точно описывает значения в мае и июне 2011 г.

У метода 2-множителей есть один существенный недостаток: он не позволяет вводить условий больше, чем число коэффициентов в модели. Из-за этого задание условий (10.53) напоминает перетягивание одеяла: исследователь вводит условие некоррелированности ошибки с факторами, но тогда он лишается права вводить другие интересующие его условия, т.е. включение дополнительных условий оказывается возможным лишь при включении дополнительных переменных, относительно которых исследователь так же может захотеть наложить какие-то условия. По на самом деле возможное решение данной проблемы существует: нужно включить в модель факторы, не влияющие линейно на у, т.е. коэффициент корреляции для которых будет близок к нулю. Их добавление не исказит оценки коэффициентов при других регрессорах, коэффициент перед этой переменной нам неважен, сам фактор нас не интересует, поэтому у нас появится возможность внести еще одно условие.

В таком случае в модели может быть эконометрическая проблема "лишних переменных", которая из-за отсутствия корреляции должна нивелироваться. Однако это решение пока до конца не изучено и носит скорее гипотетический характер.

Теперь воспользуемся выводами этого параграфа для того, чтобы понять суть МНК с дисконтированием. Систему уравнений (10.6) можно получить с помощью общей схемы оценивания методом 2-множителей (10.27), если задать 2-множители так:

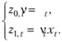(10.58)

Это означает, что, решая систему (10.6), мы получаем такие оценки коэффициентов прогнозной модели, для которой выполняются условия (10.29), применительно к рассматриваемому случаю имеющие вид

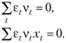(10.59)

Смысл первого уравнения системы (10.59) очевиден: поскольку веса по определению убывают в прошлое, прогнозная модель будет описывать исходный ряд данных так, что ошибки аппроксимации, убывающие в прошлое, будут больше, чем ошибки аппроксимации последних наблюдений. При этом модель обязательно будет иметь как положительные, так и отрицательные ошибки аппроксимации, иначе сумма дисконтированных ошибок аппроксимации не будет равна нулю. Модель, как следует из сказанного, хорошо описывает текущие наблюдения и плохо – прошлые, она пройдет не через среднюю арифметическую точку, а через среднюю взвешенную арифметическую точку.

Близкий к этому смысл будет иметь и второе уравнение системы (10.59): в нем представлена часть дисконтированных ковариации между ошибкой и фактором х, которая должна быть равна нулю. Это значит, что при оценке модели задается такое условие, в соответствии с которым ковариация между ошибкой и х на последних наблюдениях оказывает большее влияние на итоговую ковариацию, чем на ранних значениях.

В матричном виде МПК с дисконтированием будет эквивалентен методу 2-множителей при выполнении равенства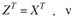

Смысл каждого из условий, вытекающих из этого равенства, будет аналогичен смыслу второго равенства в системе (10.59).

Мы вновь убедились в том, что метод 2-множителей ОСО включает не только МНК как частный случай, но и метод дисконтированного МНК, так же, как один из возможных случаев. Поэтому метод z-множителей действительно представляет общую схему оценивания коэффициентов эконометрических прогнозных моделей.

Проанализировав с помощью метода z-множителей суть дисконтированных оценок МПК, можно заметить, что с его помощью получаются и иные способы использования дисконтированных оценок. Например, применяя общий принцип учета текущих наблюдений в большей степени, чем более ранних, можно получить новые оценки коэффициентов с учетом дисконтированных данных. Например, можно задать такие 2-множители:

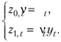(10.60)

Тогда будет получена другая система уравнений:

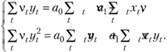(10.61)

Решая эту систему, прогнозист получит оценки адаптированной модели, ведь текущая информация используется в большей степени, чем прошлая, но эти оценки будут отличаться от оценок МНК с дисконтированием и, возможно, в некоторых случаях будут давать более точные прогнозы.

Ряд различных способов дисконтирования данных, который открывает метод z-множителей, довольно широк. Это вооружает прогнозиста новым дополнительным инструментом построения адаптивных моделей среднесрочного прогнозирования.