Модель простого экспоненциального сглаживания
Прежде всего, упростим задачу – предположим, что прогнозисту необходимо изучить некоторый временно́й ряд уt не имеющий какой-либо явно выраженной тенденции, и сделать прогноз в конце ряда на один шаг наблюдения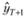 
В этом случае ему проще всего воспользоваться в качестве прогнозной модели простой средней арифметической (см. параграф 5.2):
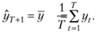(7.1)
Эта средняя арифметическая характеризует средний уровень ряда, отклонения от которого вызваны рядом причин.
В случае стационарного процесса и при нормальном распределении случайных величин эта процедура не вызывает никаких сомнений и возражений. Однако если эти условия не выполняются, то средняя арифметическая уже не будет лучшей прогнозной моделью.
В случаях с эволюционными процессами предположение об одинаковой важности всех наблюдений для получения точного прогноза не может быть адекватным. Поэтому, чтобы точнее спрогнозировать такой процесс, нужно в большей степени обращать внимание на текущие, а не на прошлые наблюдения. Например, для того, чтобы определить на завтра курс рубля по отношению к евро, текущие значения этого курса важнее, чем значения полугодовалой давности. Однако просто исключить из рассмотрения прошлые значения в общем случае также будет некорректно, так как они в себе содержат некоторую "историю изменений". Поэтому при получении точечного прогноза в случае с эволюционными процессами каждому наблюдению нужно задать некоторый вес. Тогда прогноз на один шаг может быть получен по формуле
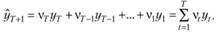(7.2)
веса при этом должны быть такими, чтобы их сумма была равна единице:
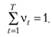(7.3)
Естественное желание учесть текущую информацию в большей степени, чем прошлую, может быть математически выражено так:
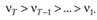
Если при этом потребовать выполнения условия (7.3), то, подставляя эти веса в (7.2), можно получить формулу взвешенной средней арифметической. В математике существует огромное количество рядов, чья сумма будет равна единице, а каждый вес будет убывать с убыванием наблюдений в прошлое, например, ряд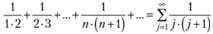 
сходится к единице, т.е. его сумма равна единице.
В принципе любой сходящийся к некоторому числу ряд можно преобразовать так, чтобы его сумма была равна единице.
Например, ряд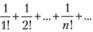 
сходится к числу е – 1. Поэтому сумма следующего ряда будет равна единице: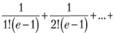 
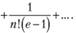
Так какой ряд из огромного множества имеющихся вариантов предпочесть для случая краткосрочного прогнозирования эволюционных процессов? В каждом случае прогнозируемый процесс своеобразен, и использовать один и тот же способ задания весов будет методологически ошибочным – в каждом отдельном случае наилучшим будет свой способ задания весов взвешенной средней. Перебирать все возможные сходящиеся к единице ряды в поиске наилучшего из них на практике не представляется возможным. Поэтому необходимо использовать некоторую универсальную процедуру, в которой, задавая один или несколько параметров, можно было бы наилучшим образом настроить взвешенную среднюю к свойствам изучаемого ряда. Такая возможность имеется при показательном характере задания весов наблюдений. Соответствующая модель была впервые предложена Р. Г. Брауном в 1956 г.[1] и независимо от него – Ч. Хольтом в 1957 г.[2]:
Здесь параметр а является единственной переменной, варьируя которую можно получить модель, пригодную для различных по характеру изменений прогнозируемого процесса. В общем случае веса в этом ряде распределяются по убывающей показательной функции. Как мы знаем, любая показательная функция может быть приведена к виду экспоненты, поэтому и этот ряд обычно называют экспоненциальным.
С помощью экспоненциально взвешенного ряда весов легко рассчитать среднее взвешенное показателя у в момент времени Т, которое будет являться прогнозной моделью про
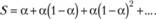(7.4)
цесса на следующий момент наблюдения (Т + 1). Обозначим это прогнозное значение через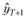 
. Подставляя в (7.2) веса (7.4), получим:
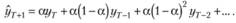
Далее, вынося за скобки общий для всех слагаемых, кроме первого, сомножитель (1 – а), получим:
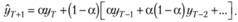
Сумма в квадратных скобках правой части полученного равенства есть не что иное, как Назад взвешенная средняя, вычисленная на множестве предыдущих значений ряда. С учетом этого получим окончательно:
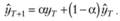(7.5)
Здесь α называется постоянной сглаживания, а (1 – α) – эквивалентной постоянной сглаживания.
Формула (7.5) оказалась очень удобной для расчетов и на Западе известна под названием "модель простого экспоненциального сглаживания" ("Simple exponential smoothing"). В отечественной литературе ее иногда называют по имени автора – "модель Брауна".
Как уже было сказано, модель имеет смысл только в том случае, когда ряд весов сходится и его сумма равна единице. В противном случае расчет по формуле (7.5) не даст взвешенную среднюю, и модель потеряет смысл взвешенной средней.
Иногда в литературе можно встретить немного другую формулу для модели экспоненциального сглаживания (к пей мы обращались в параграфе 5.1.1):
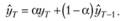(7.6)
Как видим, модель в этой форме от модели в форме (7.5) отличает лишь то, каким образом учитывается фактическое значение при формировании расчетного. Форма (7.6) чаще используется для целей сглаживания временно́го ряда, нежели в непосредственном прогнозировании, тем не менее обе формы имеют право на существование и во многом похожи по своим свойствам. Здесь и далее мы будем рассматривать модель экспоненциального сглаживания в форме (7.5).
Сразу стоит отметить, что основная цель модели Брауна – давать краткосрочные прогнозы (на 1–3 наблюдения вперед). С ее помощью можно получить прогноз и на более долгосрочную перспективу, но необходимо иметь в виду, что прогноз се тривиален. Получить этот прогноз можно, введя предположение о том, что в будущем фактические значения, которые произойдут через h наблюдений, совпадут с расчетными, полученными на наблюдении (Т + 1). В таком случае прогноз на h наблюдений, полученный методом Брауна, будет рассчитываться по формуле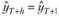 
. Как видно, со временем прогнозные значения на h наблюдений будут повторять сглаженную тенденцию, наблюдавшуюся в (Т + 1)-й момент времени.
Исходный ряд весов (7.4), предложенный Брауном, представляет собой бесконечную геометрическую прогрессию, о которой известно, что она сходится к единице, если для члена геометрической прогрессии выполняется единственное условие: модуль члена геометрической прогрессии должен быть меньше единицы[3].
Для нашего случая это условие запишется следующим образом:
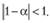(7.7)
Из этого со всей очевидностью следует, что постоянная сглаживания должна изменяться в пределах[4]:
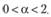(7.8)
Легко убедиться в том, что при величине постоянной сглаживания, превышающей единицу, ряд весов становится знакочередующимся, но все так же сходится к единице. Это со всей очевидностью следует из теоремы Лейбница, которая гласит, что ряд 
, где все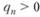 
, сходится, если последовательность {qn} невозрастающая и
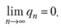(7.9)
Применительно к нашему ряду для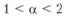 
это будет сформулировано так. Ряд значений:
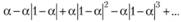(7.10)
имеет в своем составе только положительные члены. Чтобы он сходился, необходимо выполнение условия (7.9), что для исследуемого ряда примет вид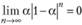 
.
Оно выполняется, поскольку выражение под модулем всегда меньше единицы в заданных границах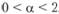 
Отметим, что еще в 1968 г. Дж. Л. Бреннер, Д. А. Д'Эспосо и А. Г. Фаулер показали в своей статье[5], что постоянная сглаживания должна лежать именно в пределах от 0 до 2, но до сих пор практически повсеместно используется более узкий промежуток – от 0 до 1, использование которого существенно обедняет модель экспоненциального сглаживания.
Итак, модель Брауна имеет право на существование как при нахождении постоянной сглаживания в пределах
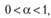(7.11)
которые назовем "классическими", так и в пределах
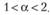(7.12)
которые мы назовем "запредельным множеством"[6].
Параметр α получил название постоянной сглаживания, потому что, как и любая взвешенная средняя, эта модель усредняет прошлые значения, т.е. сглаживает "ники" и "провалы" графика динамики показателя (рис. 7.1).
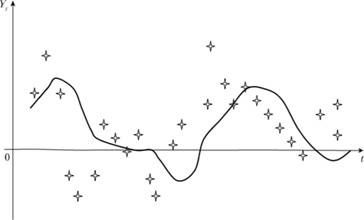
Рис. 7.1. Графическое представление сглаживания ряда с помощью модели Брауна
Определим влияние постоянной сглаживания на результаты аппроксимации динамических рядов моделью Брауна. Предположим, что постоянная сглаживания лежит в пределах от нуля до единицы (7.11) и принимает свое крайнее значение, равное нулю.
Тогда, подставив это значение в модель (7.5), получим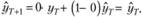 
В таком экстремальном случае модель не учитывает текущую информацию, она становится неадаптивной. Если в качестве стартовой оценки мы использовали среднюю арифметическую по какой-то части ряда (либо по всему ряду), то в этом случае мы придем к прогнозу, рассчитанному на основе этой средней величины. Однако стоит отметить, что 0 – это значение, при котором, формально говоря, модель Брауна не существует (так как ряд весов перестает сходиться к 1).
Теперь подставим в модель Брауна другое крайнее значение из классических пределов – единицу: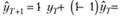 
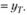Модель в таком виде становится идентичной модели Naive, рассмотренной нами в параграфе 5.2.2. В целом при таком значении постоянной сглаживания модель не учитывает прошлые значения, а полностью адаптируется к текущей информации.
Видя эти две крайние ситуации в классических пределах, можно заключить, что постоянная сглаживания характеризует степень адаптации модели Брауна к текущей информации. О том, как влияет величина постоянной сглаживания на степень адаптации модели, свидетельствует рис. 7.2, на котором изображены две сглаженные методом Брауна кривые. Первая – при а = 0,3, вторая – при а = 0,7.
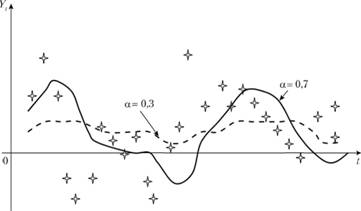
Рис. 7.2. Модель Брауна при разных значениях постоянной сглаживания
Какой же экономический смысл имеют запредельные случаи метода Брауна, определенные границами условия (7.11)? С учетом того что запредельные случаи соответствуют условию, при котором постоянная сглаживания всегда не меньше единицы, то можно ввести новую переменную в следующем виде:
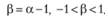(7.13)
Если теперь подставить (7.13) в исходную формулу модели Брауна (7.5) и осуществить элементарные преобразования, можно получить следующее выражение:
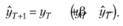(7.14)
Так как мы уже неоднократно обозначали ошибку аппроксимации как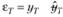 
, то модель (7.14) можно записать так:
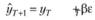(7.15)
Таким образом, появляется возможность дать смысловое толкование запредельным случаям модели Брауна.
Во-первых, следует сразу отмстить, что при этом модель полностью адаптивна к текущей информации – в формуле (7.15) текущая информация учитывается полностью, поскольку первое слагаемое формулы есть не что иное, как текущее наблюдение уt.
Во-вторых, модель становится в той или иной степени адаптивной к текущей ошибке аппроксимации – отклонению расчетных значений от фактических εt. При этом если постоянная β равна нулю, то прогнозная модель оказывается совершенно не адаптивной к текущей ошибке, а если она равна единице, то в соответствии с условием (7.15) модель краткосрочного прогноза полностью учитывает величину текущей ошибки отклонения и модель становится абсолютно адаптивной к ошибке прогноза. Случаям, когда постоянная β лежит в пределах от нуля до единицы, соответствует та или иная степень адаптивности модели к текущей ошибке отклонения фактических значений от расчетных (модель приобретает свойства самообучаемости). Тут же можно заметить, что для классического предела β принимает отрицательные значения. В таком случае модель начинает медленнее реагировать на происходящие изменения.
Поскольку постоянная сглаживания определяет то, как описывает модель Брауна прогнозируемый ряд, а значит, определяет и то, насколько точным может быть прогноз, выполненный с помощью этой модели, возникает необходимость выбора наилучшего значения величины постоянной сглаживания для каждого ряда.
В некоторых источниках можно встретить рекомендации задавать постоянную сглаживания в пределах от 0 до 0,3 – именно такой промежуток в свое время рекомендовал Браун. Однако данный промежуток слишком узок и научно нс обоснован. Более того, исследования по экспоненциальному сглаживанию показали, что априорное задание значений постоянной сглаживания ухудшает точность прогноза[7]. В наши дни для выбора оптимального значения постоянной сглаживания используют процедуру ретропрогноза, которая позволяет более эффективно подобрать значение постоянной сглаживания[8].
Для этого исходный ряд данных уt описывают с помощью модели Брауна, предварительно задав некоторое значение постоянной сглаживания α, и вычисляют ошибку ретропрогноза на каждом наблюдении: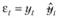 
Ошибка ретропрогноза на каждом наблюдении мало информативна с позиций поведения модели в целом. Общее представление о точности модели Брауна при заданной величине постоянной сглаживания дает некоторая обобщенная агрегированная величина: сумма квадратов отклонений, среднее абсолютное отклонение либо некоторая другая статистическая характеристика. Выбор этой характеристики определяется, прежде всего, задачами, которые ставит перед собой прогнозист. Пусть для определенности им выбран критерий минимума дисперсии:
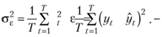(7.16)
Рассчитав для постоянной сглаживания α1 дисперсию модели Брауна относительно исходного ряда, задают другое значение постоянной сглаживания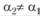
, лежащее в пределах (7.8), и вновь вычисляют ошибку рстропрогноза, а на ее основе – дисперсию ошибки.
Продолжая эту процедуру посредством изменения постоянной сглаживания в пределах ее допустимых значений, получают ряд значений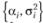 
. Поскольку дисперсия представляет собой некоторую таблично заданную функцию от постоянной сглаживания, задачу поиска оптимального значения постоянной сглаживания, при которой дисперсия ошибки будет минимальной, можно изобразить графически (рис. 7.3).
Таким образом, задача нахождения оптимального значения постоянной сглаживания сводится к элементарному поиску минимума этой функции. Решить эту задачу можно с использованием численных методов, которые в массе своей реализованы в различных статистических программах. Отметим, что чаще всего зависимость дисперсии ошибки ретро- прогноза от значений постоянной сглаживания носит характер, изображенный на рис. 7.3. Однако встречаются ситуации, когда эта зависимость имеет один или несколько локальных минимумов (рис. 7.4.). Такие ситуации для модели простого экспоненциального сглаживания крайне редки, но они могут встретиться на практике.
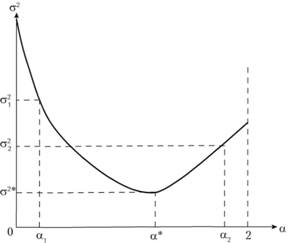
Рис. 7.3. Дисперсия ошибки ретропрогноза как функция от постоянной сглаживания
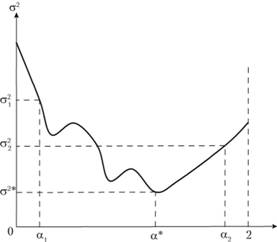
Рис. 7.4. Дисперсия ошибки ретропрогноза как функция от постоянной сглаживания с несколькими локальными минимумами
Поэтому рекомендуется поступать так. Изменяя величину постоянной сглаживания с шагом, равным 0,1, можно вычислить соответствующие дисперсии ретропрогноза. Анализ этих дисперсий позволяет определить окрестности оптимальной точки и уже в этой окрестности, используя любой известный прогнозисту численный метод, можно найти оптимальное значение постоянной сглаживания.
На практике иногда встречаются ситуации, в которых минимум дисперсии получается при α<0, что противоречит условию (7.8). Обычно это происходит в случаях с процессами, имеющими случайный или хаотический характер, в которых наилучшей оценкой прогноза является либо средняя величина, либо величина, близкая к ней. В таких ситуациях исследователю стоит задать другое начальное расчетное значение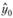 
либо использовать для прогнозирования такого ряда вместо метода Брауна какой-нибудь иной.
Как было показано выше, в случае, когда оптимальное значение постоянной сглаживания находится в классических пределах, модель адаптивна, когда же оно находится в запредельном множестве, модель не только адаптивна, но и самообучаема. Это говорит о том, что оптимальное значение постоянной сглаживания определяется свойствами исходного ряда. Чем отличается ряд, для которого наилучшей является постоянная сглаживания, лежащая в классических пределах, от другого ряда, для которого оптимальное значение постоянной сглаживания лежит в запредельном множестве? Для ответа на этот вопрос проведем модельные эксперименты на условных примерах. Рассмотрим таблицу результатов расчета рядов, генерируемых различными моделями, имеющими тенденции разного рода (табл. 7.1)[9].
Таблица 7.1
Оптимальные значения α для динамических рядов разного типа
|
Модель, с помощью которой генерировался динамический ряд |
Оптимальное значение постоянной сглаживания |
|
Отсутствие тенденций, нормальное распределение ошибок |
0,0202 |
|
Ряд с периодическим изменением уровня |
0,5321 |
|
Линейный рост |
1,5473 |
|
Линейное убывание |
1,5473 |
|
Экспоненциальный рост |
1,8547 |
|
Синусоида (три периода) |
1,4967 |
|
Парабола второй степени (вогнутая) |
1,4724 |
|
Сумма синусоиды, параболы и экспоненты |
0,2775 |
|
Логарифмическая функция |
1,2745 |
Из данных таблицы видно, что практически во всех случаях оптимальными значениями постоянных сглаживания являются значения, находящиеся в запредельном множестве от 1 до 2. Исключением является случай генерации сложного динамического ряда с помощью синусоиды, параболы и экспоненты (графически эта сумма представляет собой невозрастающую и неубывающую совокупность значений, колеблющихся вокруг некой средней величины), ряд с периодическим изменением уровня и, конечно же, случай с искусственным стационарным процессом (отсутствие тенденций). Понятно, что при разных значениях коэффициентов генерирующих функций будут получаться разные ряды, а следовательно, и разные оптимальные постоянные сглаживания, однако закономерность, показанная в табл. 7.1, сохраняется.
Теперь можно сделать необходимые обобщения, касающиеся запредельного множества Брауна. Если в процессе оптимизации постоянная сглаживания лежит в классических пределах – от 0 до 1, то это говорит о том, что перед исследователем представлен процесс либо с постоянным математическим ожиданием (стационарный процесс), либо процесс, в котором уровни ряда меняются очень редко. В таком случае модель Брауна может достаточно эффективно использоваться для прогнозирования. Если же оптимальное значение постоянной сглаживания оказалось находящимся в запредельном множестве, то это диагностирует ситуацию, когда средняя взвешенная в принципе не может использоваться в качестве оптимальной оценки прогнозного значения моделируемого процесса. Это говорит о том, что процесс вышел за рамки простой динамики. У него появилась некоторая тенденция в развитии. Ее математическое описание в наблюдаемый промежуток времени возможно с помощью одной из эконометрических моделей. В этом случае модель, которая лучше всех описывает динамику прогнозируемого экономического процесса, берется за основу и с ее помощью применяется соответствующая модификация метода Брауна.
Тем не менее, если перед исследователем стоит задача дать прогноз по модели Брауна, более точным будет прогноз на основе постоянной сглаживания, подобранной из полного множества (7.8), нежели из классического[10].
Стоит сказать и о других критериях, использующихся при подборе постоянной сглаживания. Помимо критерия минимума дисперсии ошибки, в случаях, когда в ряде данных наблюдаются выбросы, рекомендуется осуществлять подбор параметров на основе минимума средней абсолютной ошибки:
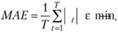(7.17)
Данный критерий более устойчив к "выбросам" и позволяет получить более робастное значение[11].
Итак, модель простого экспоненциального сглаживания оказывается очень удобной в практическом использовании для целей краткосрочного прогнозирования как стационарных, так и нестационарных процессов. Однако главной причиной, почему в литературе постоянную сглаживания повсеместно ограничивают классическим пределом, является проблема с интерпретацией значений, выходящих за границы (7.8). В данном случае мы сталкиваемся с ситуацией, когда желание интерпретировать модель значительно ее ограничивает и обедняет. Рассмотрим этот вопрос подробнее.
В общем виде модель Брауна принято записывать как (7.5):
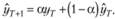(7.18)
Именно в таком виде модель Брауна и стала популярной, и именно в таком виде появляется соблазн дать постоянной сглаживания следующую интерпретацию (которая превалирует в среде экономистов): а представляет собой некоторую среднюю взвешенную, служащую для формирования прогнозного значения. Таким образом, прогноз складывается из двух частей: из части фактического значения, полученного на наблюдении ί, и части, спрогнозированной на это же наблюдение t. В такой трактовке очевидно, что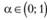
, так как подразумевается наличие средней между двумя значениями. Данной трактовки модели придерживаются многие экономисты.
Графически формирование прогнозного значения в соответствии с формулой (7.18) представлено на рис. 7.5: точка III считается как средневзвешенная фактического значения I и прогнозного II, ее значение как раз и становится прогнозом – точкой IV. Далее берется средневзвешенная между точками IV и V, получается новая средняя (точка VI) и новый прогноз (точка VII) и т.д. Причем а в данной интерпретации регулирует распределение весов между фактом и прогнозом.
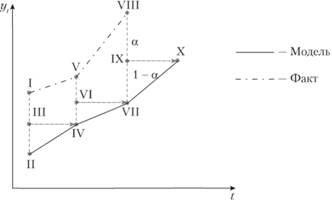
Рис. 7.5. Графическое представление механизма формирования прогноза в модели (7.18)
Однако в данном случае мы сталкиваемся с ситуацией, в которой такая трактовка модели ее только ограничивает.
Если раскрыть скобки во втором множителе правой части равенства (7.18) и перегруппировать слагаемые, то можно получить иную форму записи модели Брауна:
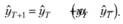(7.19)
В таком виде у нее более явно видны адаптивные черты: прогнозное значение формируется на основе предыдущего спрогнозированного, а а выступает некоторым коэффициентом адаптации модели к новой поступающей информации. В этом случае степень адаптации может быть любой: модель может адаптироваться незначительно и отсеивать поступающие "шумы" (когда а мал и, например, составляет 0,3) или достаточно быстро адаптироваться к поступающей информации в случае, когда в процессе происходят качественные изменения (когда α больше 1, например 1,7).
Более того, поскольку выражение в скобках второго слагаемого правой части равенства (7.19) есть не что иное, как текущая ошибка аппроксимации, то модель Брауна может быть записана и так:
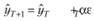(7.20)
Первая составляющая в (7.20) представляет собой среднюю взвешенную предыдущих значений, т.е. несет в себе информацию обо всех предыдущих значениях изучаемого ряда. Второе слагаемое, представляющее собой произведение постоянной сглаживания на текущую ошибку аппроксимации, характеризует способность модели учитывать текущую ошибку аппроксимации. Таким образом, модель Брауна обладает способностью адаптироваться к текущим отклонениям от некоторого сложившегося уровня ряда.
Такая форма, стоит заметить, обычно носит название формы "коррекции ошибок", так как модель в таком виде корректирует свое значение к полученной на предыдущем наблюдении ошибке.
В целом эта адаптация к ошибке происходит так. В случае, когда фактическое значение наблюдаемого ряда выше расчетного, ошибка аппроксимации имеет положительный знак и средняя арифметическая увеличивается на откорректированную с помощью постоянной сглаживания величину этого отклонения. Если текущая ошибка аппроксимации отрицательна, средняя взвешенная уменьшается на откорректированную величину ошибки аппроксимации. Таким образом, расчетные значения как бы "подтягиваются" к текущему значению. В этом и проявляется суть адаптации модели Брауна. Графическое представление этой трактовки дано на рис. 7.6.
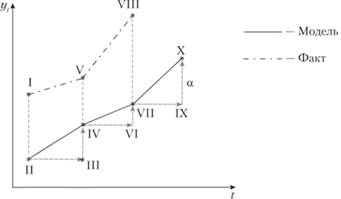
Рис. 7.6. Графическое представление механизма адаптации в модели (7.20)
Здесь расчетное значение II берется за базу для прогноза на следующем наблюдении и переносится в точку III, которая затем корректируется на величину отклонения фактического значения I от расчетного II. В итоге прогнозное значение из точки III "переходит" в точку IV, которая, в свою очередь, становится базой для следующего прогноза (точка VI) и т.д.
Модель Брауна можно представить и в другом виде. Так, если обратиться к формуле (7.15):
(7.21)
то мы придем к новой форме, по-прежнему математически тождественной формам (7.18) и (7.20). Однако благодаря такому представлению полученную модель можно в очередной раз трактовать несколько иначе. Для наглядности рассмотрим трактовку этой формы на рис. 7.7.
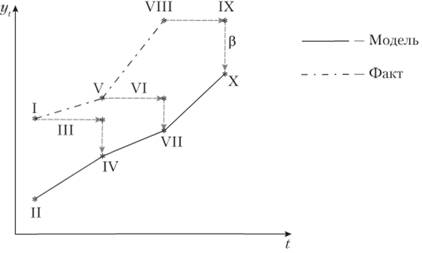
Рис. 7.7. Графическое представление механизма адаптации в модели (7.21)
По своей логике этот механизм напоминает описанный для рисунка 7.6, однако у него есть некоторые отличия. Так, модель изначально формируется исходя из предыдущего фактического значения, а не из предыдущего расчетного (значение точки I переносится на следующее наблюдение в точку III), которое затем корректируется на величину отклонения факта (точка I) от прогноза (точка II) на предыдущем наблюдении пропорционально значению коэффициента β.
Для классических пределов изменения постоянной сглаживания от нуля до единицы коэффициент β=α-1 лежит в пределах (-1,0]. При положительном знаке текущей ошибки аппроксимации фактическое значение, выступающее в качестве ориентира для прогноза, уменьшается на откорректированную величину текущей ошибки аппроксимации εT. Это значит, что прогноз по модели Брауна при постоянной сглаживания, лежащей в классических пределах, обладает свойством инерционности – следующее прогнозное значение никогда не достигнет уровня уже имеющегося текущего.
В случае запредельного множества (7.12) коэффициент β лежит в пределах [0,1). В таком случае при положительном отклонении фактического значения от расчетного модель предполагает дальнейшее увеличение показателя, превышающее достигнутый уровень. Поэтому фактическое значение увеличивается на величину текущего отклонения, скорректированного на поправочный коэффициент β.
Значит, в классических границах изменения постоянной сглаживания модель Брауна инерционна, а в запредельных случаях инерционность модели уменьшается. Зная это свойство, можно дать интерпретацию модели Брауна.
В классических пределах, когда постоянная сглаживания лежит в промежутке от нуля до единицы, модель отражает изменяющиеся, но инерционные эволюционные процессы, в которых изменения протекают с небольшой скоростью.
В запредельном множестве, когда постоянная сглаживания лежит в пределах от единицы до двух, модель описывает процессы с малой инерционностью, когда качественные изменения в исследуемом объекте происходят быстро.