Моделирование сезонных колебаний с использованием фиктивных переменных
В стороне от методов сезонной декомпозиции стоит метод учета сезонных колебаний в регрессионных моделях с помощью фиктивных переменных. Метод фиктивных переменных был рассмотрен нами подробно в параграфе 4.6. Здесь мы рассмотрим один из вариантов его применения на практике.
Как мы отмечали ранее, фиктивные переменные могут включаться в регрессию двумя способами:
1) в константу, путем простого добавления соответствующих переменных;
2) в угол наклона, путем перемножения фиктивных переменных на факторы и включения новых полученных переменных в регрессию.
При моделировании сезонности эти способы дают совершенно разные результаты. Первый способ фактически соответствует построению модели с аддитивной сезонностью, в то время как второй – соответствует построению модели с мультипликативной сезонностью.
Рассмотрим для начала первый способ включения фиктивных переменных.
Пусть перед исследователем стоит задача построить аддитивную модель с сезонностью вида (6.1) 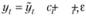 где в качестве
где в качестве 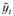 может выступать как некоторый тренд, так и регрессионная модель вида
может выступать как некоторый тренд, так и регрессионная модель вида
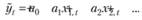 (6.24)
(6.24)
Для учета аддитивной сезонности в таком случае в модель можно ввести s-1 фиктивную переменную. Например, в случае с квартальными данными в модель нужно будет включить три фиктивные переменные, соответствующие кварталам:
1) season1 = 1 – если данное наблюдение относится к первому кварталу;
2) season2 = 1 – если данное наблюдение относится ко второму кварталу;
3) season3 = 1 – если данное наблюдение относится к третьему кварталу.
Тогда регрессионная модель будет иметь следующий вид;
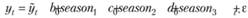 (6.25)
(6.25)
Коэффициенты такой модели могут быть оценены простым МНК.
Эталоном в данном случае выступает четвертый квартал, для которого модель (6.25) будет принимать вид 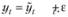
Для всех остальных кварталов будет меняться уровень ряда на величину коэффициента перед соответствующей фиктивной переменной. Такое включение фиктивных переменных будет приводить к учету аддитивной сезонности: каждый первый квартал года значение уt будет выше значения 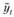 на одну и ту же фиксированную величину b0, что в принципе соответствует простому сезонному коэффициенту для этого же квартала, получаемому в случае с классической декомпозицией. Единственное различие в коэффициентах будет заключаться в точке отсчета. Как мы обсуждали ранее, фиктивные переменные характеризуют различия в категориях относительно выбранного эталона. Сезонные же коэффициенты считаются относительно некой средней сглаженной линии. Значения сезонных коэффициентов и коэффициентов при фиктивных переменных будут различными, однако зависимости они будут моделировать одни и те же, но схожим принципам.
на одну и ту же фиксированную величину b0, что в принципе соответствует простому сезонному коэффициенту для этого же квартала, получаемому в случае с классической декомпозицией. Единственное различие в коэффициентах будет заключаться в точке отсчета. Как мы обсуждали ранее, фиктивные переменные характеризуют различия в категориях относительно выбранного эталона. Сезонные же коэффициенты считаются относительно некой средней сглаженной линии. Значения сезонных коэффициентов и коэффициентов при фиктивных переменных будут различными, однако зависимости они будут моделировать одни и те же, но схожим принципам.
Моделирование мультипликативной сезонности с помощью фиктивных переменных возможно двумя методами:
1. Перейти к логарифмам, после чего включить фиктивные переменные. В таком случае мы получим модель:
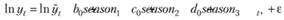 (6.26)
(6.26)
которая, как мы знаем, будет соответствовать модели:
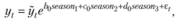 (6.27)
(6.27)
в которой сезонность уже действительно учтена мультипликативно. Однако подобное включение подразумевает предварительную оценку 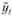 , например, по десезонализированному ряду, что заставляет нас обратиться к одному из методов сезонной декомпозиции.
, например, по десезонализированному ряду, что заставляет нас обратиться к одному из методов сезонной декомпозиции.
2. Включить фиктивные переменные в угол наклона факторов модели.
В этом случае предварительно надо понять, от какого фактора может зависеть величина амплитуды. В модели вида (6.24) сезонность может, например, расти с ростом x1 либо со снижением х2, либо с изменением другого фактора. Выяснить, с динамикой какого из факторов связана сезонность, на практике может быть проблематично. Однако если мы строим модель тренда, то сезонность можем учесть мультипликативно, добавив фиктивные переменные в угол наклона. Например, если мы имеем дело с простой линейной моделью:
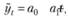 (6.28)
(6.28)
то модель с мультипликативной сезонностью будет иметь вид
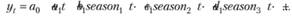 (6.29)
(6.29)
В таком случае с ростом значения t значение у по сезонам будет расти. Например, для квартальных данных на первом наблюдении в первый сезон значение у будет выше эталонного на b1•1, а на пятом (год спустя) – выше эталона на b1•5.
Графически простая модель тренда (6.28) с фиктивными переменными может быть представлена следующим образом на примере ряда № 2568 (рис. 6.19).
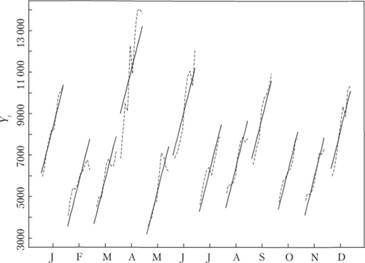
Рис. 6.19. Ряд № 2568 в динамике по месяцам (пунктирные линии) и его аппроксимация (сплошные линии) с помощью модели линейного тренда с фиктивными переменными
Как видим по рис. 6.19, каждый год по месяцам в ряде № 2568 наблюдается тенденция к росту. Поскольку ряд Ха 2568 трендово стационарен, его можно было описать простой моделью тренда с добавлением фиктивных переменных (по аналогии с (6.29)). На рис. 6.19 показано, как в таком случае тенденция была описана по месяцам. На рис. 6.20 изображена часть ряда Ха 2568 с упомянутой моделью с фиктивными переменными.
Рисунок показывает, что собой представляет модель с фиктивными переменными. Прямыми пунктирными линиями показаны модели трендов для апреля и мая каждого года. Как видим, по каждому из периодов по годам наблюдается простой линейный рост. Единственное, что происходит – от месяца к месяцу меняется константа, которая как раз и зависит от значения коэффициента при фиктивной переменной.
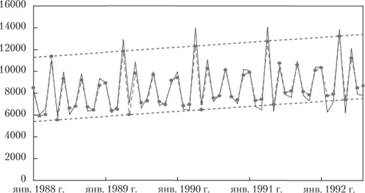
Рис. 6.20. Часть ряда № 2568 (сплошные гонкие линии) и его аппроксимация (пунктирные линии с точками) с помощью модели линейного тренда с фиктивными переменными
Подводя итог рассмотрению моделирования сезонности с помощью фиктивных переменных, можно выделить следующие преимущества и недостатки метода.
Преимущества:
1. Метод не требует "разложения" ряда на части, а значит, не требует и определения того, как именно сглаживать отдельные части ряда.
2. При использовании метода не происходит потерь наблюдений (как в случае с методом классической декомпозиции).
3. Метод позволяет включить сезонность в любую регрессионную модель, а нс только в модель тренда, что может быть полезно в случае, если мы пытаемся спрогнозировать какой-то показатель на основе значений другого известного нам показателя.
4. Метод прост в реализации: достаточно задать вид функции, определить, как именно включать фиктивные переменные, и рассчитать оценки коэффициентов методом наименьших квадратов.
Недостатки:
1. Метод подразумевает усреднение всех сезонных коэффициентов. Он не допускает возможности эволюционного изменения сезонных составляющих во времени.
2. Метод не учитывает возможные "выбросы" – их можно учесть только вручную, задав предварительно соответствующие веса каждому наблюдению и рассчитав оценки модели взвешенным МПК.
3. Для построения модели таким методом требуется предварительно выбрать вид функции, которая лучше всего опишет данный процесс. В случае с простыми трендовыми моделями это может быть затруднительно, особенно в ситуациях, когда трендовая компонента эволюционирует во времени.