Методы оптимизации на основе теоремы Куна — Таккера

Рассмотренная теорема Куна — Таккера позволяет сформулировать ряд методов условной оптимизации.

Метод вспомогательной переменной

Обсудим решение следующей задачи квадратичного программирования: вычислить

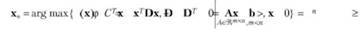
с использованием следствий из теоремы Куна — Таккера. Функция Лагранжа для данной задачи имеет вид

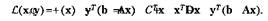
Градиенты функции Лагранжа по переменным хиу равны

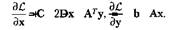
Условия Куна — Таккера с учетом дифференциальных соотношений даны в табл. 2.4.

Таблица 2.4. Условия Куна — Таккера с учетом дифференциальных соотношений

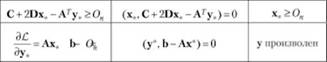
Введем вспомогательную переменную У> 0, такую, что

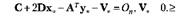
Тогда условия Куна — Таккера примут вид, данный в табл. 2.5.

Как следует из данных табл. 2.5, для отыскания оптимального решения (седловой точки функции Лагранжа) следует решить систему равенств (неравенств)

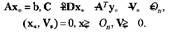
Таблица 2.5. Условия Куна — Таккера с учетом вспомогательной переменной

Таким образом, метод позволяет свести задачу условной минимизации квадратичного функционала к решению системы линейных равенств и неравенств.

Метод Била

Рассмотрим обобщенную задачу выпуклого квадратичного программирования (по сравнению с задачей (2.6.1) подпараграфа 2.6.1): вычислить

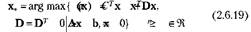
Предположим, что систему ограничений задачи (2.6.19) удается разрешить относительно п первых компонент, т.е. из ограничений задачи Ах =А{х^ + А^х = Ьт можно определить

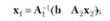
где х — свободные переменные.

Представим далее (р(х) как функцию свободных переменных. Тогда функционал определит новую задачу математического программирования, в которой минимизируемый квадратичный функционал данной задачи принимает следующий преобразованный вид:

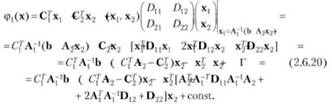
Выражение в квадратных скобках в (2.6.20) есть не что иное, как (Э<р/Эх)/2. Если (Э<р/Эх)>0,то полученное решение х = (х,, х)г оптимально. Если некоторые компоненты (Эф/Эх)<0, то можно увеличить значение ф(х). При увеличении некоторой переменной х возможны две ситуации.

1. Некоторая переменная ^базисных переменных обращается в нуль, и в дальнейшем ее увеличение невозможно. Тогда можно найти значение хт+,, при котором хк = О, как в симплекс-методе (см. параграф 2.3). Затем надо сделать пересчет переменных и снова проверить решение на оптимальность.

2. Производная Эф/Элгш+1=0 внутри допустимой области. Тогда из этого условия можно найти хт+1, вычислить новое решение, а затем снова проверить новое решение на оптимальность в соответствии с условиями Куна — Таккера.

Таким образом, описанная идея метода Била содержит проверку на оптимальность в соответствии с условиями Куна — Таккера и пересчет переменных па основе соотношений симплекс-метода. При этом вычисления проводятся в пространстве меньшей размерности в результате введения свободных переменных.

Метод Баранкина и Дорфмана

Рассмотрим задачу условной минимизации квадратичного программирования: вычислить вектор

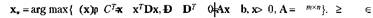
Условия Куна — Таккера для данной задачи имеют вид, представленный в табл. 2.6.

Таблица 2.6. Условия Куна — Таккера в задаче Баранкина и Дорфмана

Идея метода состоит в применении к ограничениям линейного типа данной задачи ряда симплексных преобразований, в результате которых достигается выполнение условия х'"У* = 0. При проведении симплексных преобразований проверяется одновременно допустимость решений.

Таким образом, условия Куна — Таккера порождают ряд вычислительных схем, сочетающих аналитические условия и вычислительные процедуры.

Метод проекции градиента и условные нелинейные оценки

Метод проекции градиента является универсальным для задач выпуклой минимизации, использует проецирование на допустимое множество в процессе вычислений. Рассмотрим алгоритмы, использующие проекции для различных ограничений.