Методы однокритериальной оптимизации

В практической деятельности мы часто говорим об оптимальной структуре организации, оптимальном управлении на производстве, оптимальном планировании деятельности. В предыдущих параграфах мы уже неоднократно сталкивались с постановкой и решением задач оптимизации. Данный параграф призван расширить и систематизировать материал по данной теме. В первой части рассмотрены методы однокритериальной оптимизации, во второй исследованы возможности многокритериальной оценки СЭС, в третьей рассмотрены методы теории активных систем.

Задача оптимизации функции многих переменных при отсутствии ограничений. Формальная постановка задачи оптимизации при отсутствии ограничений Вперед: найти значения п переменных xi, i = 1, 2, ..., п, заданных в евклидовом пространстве Еп, при которых достигается экстремум некоторой непрерывно дифференцируемой функции

F = F(x) = F(x1., ..., xn) (5.13)

вектора независимых переменных х = (x1., ..., xn).

Очевидно, что максимизация целевой функции F(x) равносильна максимизации функции а + bF(x) при b > 0 и ее минимизации при b < 0. То есть для упрощения задачи постоянным слагаемым целевой функции и положительным множителем можно пренебречь, а отрицательный множитель использовать для преобразования задачи максимизации в задачу минимизации. Рассмотренная задача хорошо известна читателям еще из школьного курса математики. Поэтому в данном параграфе ограничимся лишь рассмотрением конкретного примера, проливающего свет на некоторые дополнительные обстоятельства, знание которых необходимо при оптимизации экономических задач.

Задача 5.8. Рассмотрим наиболее простую детерминированную постановку задачи планирования ресурсов. Пусть в течение заданного периода Т (например, год) расходуется количество ресурсов Q, которое регулярно пополняется.

Требуется определить оптимальное число п пополнений ресурса с точки зрения минимизации затрат на хранение ресурса и разовые затраты на его пополнение. Разовое пополнение ресурса составляет количество . Его среднее значение от момента поступления до израсходования равно q/2. Если расходы на ОГЛАВЛЕНИЕ ресурса составляют С, на единицу количества, то расходы за время Т на ОГЛАВЛЕНИЕ равны

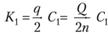
Пусть разовые расходы на пополнение ресурса составляют С2. Тогда расходы на пополнение за плановый период К2=п•С2. Общие расходы (рис. 5.4) равны сумме расходов на ОГЛАВЛЕНИЕ и пополнение ресурсов:

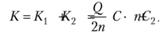(5.14)

Согласно принятой постановке следует минимизировать функцию (5.14) по аргументу п. Оптимальное значение п определяется из уравнения

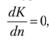
рис. 5.4 графически иллюстрирует алгоритм оптимизации.

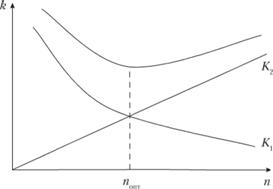
Рис. 5.4. Графики стоимостей:

К – общая стоимость; К1 – стоимость хранения; К2 – стоимость завоза ресурсов; п – число пополнений ресурса; попт – оптимальное число пополнений ресурса

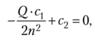
откуда

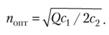(5.15)

Вычислим оптимальную величину пополнения ресурса

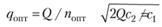(5.16)

и минимальные затраты

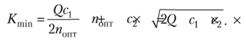(5.17)

На рис. 5.5 представлены схемы пополнения и расхода ресурсов в зависимости от величины пополняемого ресурса. В случае а) объем пополнения в два раза меньше и в два раза чаще следует пополнять ресурс. Соотношения (5.15)-(5.17) определяют, соответственно, оптимальные значения числа пополнений ресурса, его разового объема и суммарных затрат на хранение и пополнение.

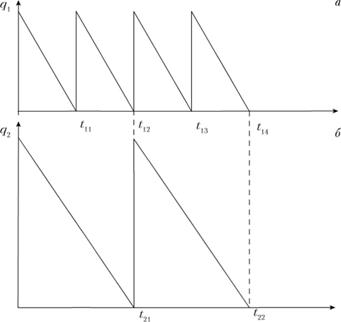
Рис. 5.5. Графики расхода ресурса в зависимости от объема накопления

Метод множителей Лагранжа. Одним из наиболее эффективных методов решения классических задач программирования с ограничениями является метод множителей Лагранжа. Этому методу в теории оптимального управления придается особое значение, поскольку он неоднократно используется в качестве основного подхода к решению почти всех видов задач оптимизации. Кроме того, с его помощью можно получить ценную информацию о том, в какой степени оптимальное значение целевой функции чувствительно к изменениям констант ограничений. Последнее обстоятельство позволяет придавать множителям Лагранжа важный экономический смысл в задачах рациональной экономической деятельности.

Для первоначального ознакомления с указанным методом рассмотрим задачу на максимум с одной степенью свободы, в которой число независимых переменных в критерии п = 2, а число ограничений т = 1, т.е. нужно найти

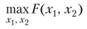(5.18)

при условии, что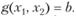

Например: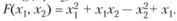

Допустим, что в точке 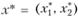существует локальное решение задачи и что в этой точке одна из частных производных функции ограничений не равна нулю.

Пусть переменные занумерованы так, что

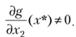(5.19)

Тогда выражение для полного дифференциала

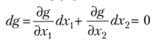(5.20)

можно в окрестности х* записать в виде

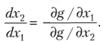(5.21)

Выражение (5.20) следует из сути ограничения: g = const.

Решая это уравнение, представим х2 как функцию х1:

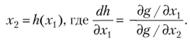(5.22)

Задача 5.9. Пусть ограничение имеет вид: 2x1 + х2 = 5. Тогда (5.21) принимает вид: dx2/ dx1 = –2 или dx1 / dx2 = –0,5, а 5 – х2 = -2x1.

Теперь исходную задачу можно представить как задачу оптимизации функции одной переменной при отсутствии ограничений, т.е. найти

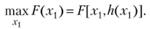(5.23)

В нашем примере: 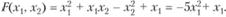Теперь легко найти точку экстремума х, =0,1.

Согласно результатам, полученным ранее, условие первого порядка для существования локального максимума функции состоит в том, что

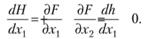(5.24)

Используя выражение (5.22), получим

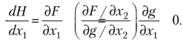(5.25)

Очевидно, что также справедливо

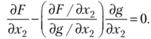(5.26)

Введем новую переменную у:

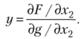(5.27)

Из условия существования локального максимума необходимо следует, что

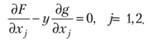(5.28)

При у = 1 имеем тождество, а при у = 2 оно совпадает с выражением (5.27) или, исключая из этих выражений переменную у,

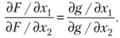(5.29)

В нашем случае простой расчет приводит к х2 = –0,2 или х1 = 0,1, что хорошо согласуется с уже полученным решением.

Отметим теперь одно весьма существенное обстоятельство, а именно: необходимые условия (5.28) и исходное ограничение можно было бы получить как условия стационарности экстремума некоторой функции без ограничений некоторой точки функции

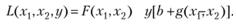(5.30)

Эти условия состоят в том, что

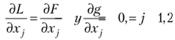(5.31)

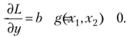(5.32)

Переменную у называют множителем Лагранжа, а функцию L – функцией Лагранжа (лагранжианом).

Итак, теперь для практического использования метода нам понадобятся только формулы (5.23), (5.30)-(5.32).

Множители Лагранжа, соответствующие решению задачи, измеряют чувствительность оптимального значения целевой функции к изменению констант ограничений b. В нашем случае это следует из выражения (5.27).

Методы линейного, нелинейного, динамического, целочисленного программирования. Метод линейного программирования ранее уже проиллюстрирован на примере распределения учебной нагрузки между вузами в параграфе 5.2. Его отличительная особенность состоит в том, что критерии оптимизации и ограничения – линейные функции. То есть критерий не имеет экстремума в общепринятом смысле, а максимальное или минимальное значение его достигается на границе области, задаваемой ограничениями. Методы линейного программирования осуществляют рациональный перебор вершин многоугольника допустимой области и выбирают из них те, которые соответствуют поставленной задаче.

Задача нелинейного программирования возникает, если или ограничения, или критерий – выпуклые (вогнутые) функции. В этом случае максимальные (минимальные) значения критерия могут достигаться как на границе области (как в задаче линейного программирования), так и внутри ее.

Задачи линейного и нелинейного программирования достаточно хорошо разработаны и изучаются во многих курсах, что позволяет нам не уделять этому вопросу много внимания.

Методы динамического программирования учитывают роль фактора времени в оптимизационных задачах. Рассмотрим особенности метода на конкретном примере.

Задача 5.10. В качестве примера возьмем задачу планирования работы железнодорожной станции, заключающуюся в выборе оптимальной очередности обработки поступивших на станцию поездов. Введем следующие обозначения: Т – горизонт планирования (максимальный период времени, на который удается построить план); N1 – количество операций, которое необходимо выполнить для полной переработки поезда на станции; N2 – количество типов поездов, различающихся по времени выполнения операций; tв (n1, п2) – время выполнения n1-й операции для п2-го типа поезда, 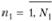,; t0 (n1, п2) – время ожидания n1-го поезда на п2 операции; it – номер первого поезда в момент времени t – расчета (корректировки) плана; it+T – номер последнего поезда в интервале планирования [t, t + Т].

Показателем качества работы станции является суммарное время нахождения вагонов на станции в интервале времени [t, t + Т]:

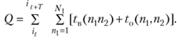(5.33)

Очевидно, что это время зависит от текущего состояния станции (общего количества и числа свободных путей, количества поездов, ожидающих выполнения той или иной операции, и т.д.) и от последовательности управления d = (d1, d2, ..., dk), отождествляемой с порядком подачи поездов на обслуживание. Показатель качества Q достигает минимальной величины, если

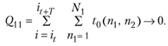(5.34)

Условие (5.34) в большинстве случаев не может быть выполнено, поэтому решается задача нахождения

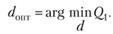(5.35)

Решение этой задачи может быть найдено методами динамического программирования.

Каждое очередное прибытие поезда определяет начало нового цикла решения задачи по формуле (5.35). При этом учитывается изменение текущей ситуации и производится смещение горизонта оптимизации.

Метод динамического программирования можно использовать для решения весьма широкого круга задач, включая задачи распределения ресурсов, замены и управления запасами, задачи о загрузке. Характерным для динамического программирования является подход к решению задачи по этапам, с каждым из которых ассоциирована одна управляемая переменная. Набор рекуррентных вычислительных процедур, связывающих различные этапы, обеспечивает получение допустимого оптимального решения задачи в целом при достижении последнего этапа. Первые задачи, которые привели к появлению вычислительного метода, были динамическими задачами управления запасами.

В экономических процессах управление заключается в распределении и перераспределении средств на каждом этапе. Например, выпуск продукции любым предприятием – управляемый процесс, так как он определяется изменением состава оборудования, объемом поставок сырья, величиной финансирования и т.д. Совокупность решений, принимаемых в начале каждого года планируемого периода по обеспечению предприятия сырьем, замене оборудования, размерам финансирования и т.д., является управлением. Казалось бы, для получения максимального объема выпускаемой продукции проще всего вложить максимально возможное количество средств и использовать на полную мощность оборудование. Но это привело бы к быстрому изнашиванию оборудования и, как следствие, к уменьшению выпуска продукции. Следовательно, выпуск продукции надо спланировать так, чтобы избежать нежелательных эффектов. Необходимо предусмотреть мероприятия, обеспечивающие пополнение оборудования по мере изнашивания, т.е. по периодам времени. Последнее, хотя и приводит к уменьшению первоначального объема выпускаемой продукции, но обеспечивает в дальнейшем возможность расширения производства. Таким образом, экономический процесс выпуска продукции можно считать состоящим из нескольких этапов (шагов), на каждом из которых осуществляется влияние на его развитие.

Началом этапа (шага) управляемого процесса считается момент принятия решения (о величине капитальных вложений, о замене оборудования определенного вида и т.д.). Под этапом обычно понимают хозяйственный год.

Планируя многоэтапный процесс, исходят из интересов всего процесса в целом, т.е. при принятии решения на отдельном этапе всегда необходимо иметь в виду конечную цель.

Таким образом, сущность динамического программирования состоит в замене решения данной k-шаговой задачи последовательностью одношаговых задач.

Назовем главные признаки (свойства) задач, к которым можно применить метод динамического программирования:

• задача должна допускать интерпретацию как k-шаговый процесс принятия решений;

• задача должна быть определена для любого числа шагов и иметь структуру, не зависящую от их числа;

• для k-шаговой задачи должно быть задано некоторое множество параметров, описывающих состояние системы, от которых зависят оптимальные значения переменных. Это множество не должно изменяться при увеличении числа шагов;

• выбор решения (стратегии управления) на k-м шаге не должен влиять на предыдущие решения, кроме необходимого пересчета переменных.

Задача 5.11. Приведем еще один пример. Пусть планируется деятельность некоторой системы S промышленных предприятий Р1, Р2, ..., Рn на некоторый период времени Т, состоящий из k хозяйственных лет ti (i = 1, 2, ..., k), причем

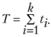
В начале периода Т на развитие предприятий выделены основные средства D. В начале каждого хозяйственного года производится финансирование всей системы предприятий, т.е. выделяется доля основных средств. Известны первоначальное состояние системы S0, характеризуемое количеством средств, уже вложенных в предприятия, и конечное состояние Sk, характеризуемое всей дополнительно вложенной суммой D. Как следует распределить по предприятиям и годам основные средства D, чтобы к концу периода Т суммарный доход W от всей системы предприятий был максимальным?

Решение. Обозначим через сумму, выделяемую в начале i-го года j-му предприятию (i = 1, 2, .... k; j = 1, 2, ..., n). Предположим, что средства на i-м этапе распределены, т.е. выбрано определенное управление U, которое состоит в том, что в начале i-го года предприятию Р, выделены средства хi1, предприятию Р2 – средства xi2 и т.д. Тогда вектор Ui = (xi1, xi2, ..., xin) определяет распределение средств на i-м этапе. Совокупность выделенных средств (управлений) на k шагах выразится системой векторов n-мерного векторного пространства

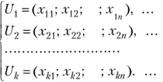
Суммарный доход за k лет зависит от совокупности управлений, т.е. является функцией от U1, U2, ..„Up.

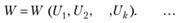
Задача состоит в следующем: на каждом этапе необходимо выбрать такое управление, чтобы суммарный доход от всей системы предприятий был максимальным.

Примечание. В общем случае начальное S0 и конечное Sk, состояния системы точно не задаются, а указывается целая область начальных S0 и конечных Sk, состояний.

Сформулированную задачу, на первый взгляд, можно решить непосредственно, объединив все этапы. Действительно, W можно рассматривать как функцию от элементов управлений на каждом этане:

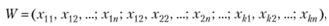
т.е. как функцию многих переменных. Теперь решение задачи заключается в нахождении такой совокупности значений аргументов Хij, при которой функция W достигает максимального значения. Казалось бы, найдя частные производные функции W по всем аргументам, приравняв их к нулю и решив уравнение

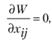
получим значения xij, при которых функция W имеет локальный максимум.

Однако этот метод имеет существенные недостатки: во-первых, при большом количестве этапов решение полученной системы довольно громоздко; во-вторых, с его помощью можно найти критические точки только внутри области, так как метод не позволяет исследовать пограничные точки; в-третьих, метод вообще неприменим, если xij – дискретные величины.

Таким образом, для большинства задач динамического программирования классические методы анализа или вариационного исчисления оказываются неэффективными, поскольку приводят первоначально поставленную задачу отыскания максимального значения функции к задаче, которая нс проще, а сложнее исходной. Динамическое программирование, используя поэтапное планирование, позволяет не только упростить решение задач, но и решить те из них, к которым нельзя применить методы математического анализа. Упрощение решения достигается за счет значительного уменьшения количества исследуемых вариантов, так как вместо того, чтобы один раз решать сложную многовариантную задачу, метод поэтапного планирования предполагает многократное решение относительно простых задач.

Однако динамическое программирование имеет и свои недостатки. В отличие от линейного программирования, в котором симплексный метод является универсальным, в динамическом программировании такого метода не существует. Каждая задача имеет свои трудности, и в каждом случае необходимо найти наиболее подходящую методику решения. Недостаток динамического программирования заключается также в трудоемкости решения многомерных задач. При очень большом числе переменных решение задачи даже на современных компьютерах ограничивается памятью и быстродействием машины. Например, если для исследования каждой переменной одномерной задачи требуется 10 шагов, то в двумерной задаче их количество увеличивается до 100, в трехмерной – до 1000 и т.д.

Отыскание оптимальной стратегии принятия набора последовательных решений в большинстве случаев производится следующим образом: сначала осуществляется выбор последнего во времени решения, затем при движении в направлении, обратном течению времени, выбираются все остальные решения вплоть до исходного.

Для реализации такого метода необходимо выяснить все ситуации, в которых может происходить выбор последнего решения. Обычно условия, в которых принимается решение, называют "состоянием" системы. Состояние системы – это описание системы, позволяющее, учитывая будущие решения, предсказать ее поведение. Нет необходимости выяснять, как возникло то или иное состояние или каковы были предшествующие решения. Это позволяет последовательно выбирать всего по одному решению в каждый момент времени. Независимо от того, отыскивают оптимальные решения с помощью табличного метода и последующего поиска или аналитическим путем, обычно быстрее и выгоднее производить выбор по одному решению в один момент времени, переходя затем к следующему моменту и т.д. К сожалению, таким методом можно исследовать не все процессы принятия решений. Необходимым условием применения метода динамического программирования является аддитивность цен всех решений, а также независимость будущих результатов от предыстории того или иного состояния.

Если число решений очень велико, то можно построить относительные оценки состояний так, чтобы оценки, отвечающие каждой паре последовательных решений, отличались друг от друга на постоянную величину, представляющую собой средний "доход" на решение. Также можно выполнять дисконтирование доходов от будущих решений. Необходимость в этом иногда появляется в том случае, когда решение принимаются редко, скажем раз в году. Тогда уже не нужно рассматривать последовательно 1-, 2-, 3-е и последующие решения, чтобы достичь решения с наибольшим номером. Вместо этого можно непосредственно оперировать функциональным уравнением, что, как правило, дает существенную выгоду с точки зрения сокращения объема вычислений.

Следующий пример иллюстрирует постановку задачи целочисленного программирования.

Задача 5.12. Рассмотрим некоторую систему (технико-технологическую, социально-экономическую), в которой поэтапно выполняются некоторые операции. Существует вероятность срыва отдельного этапа. От этого зависит успех функционирования системы. Следует повысить надежность системы путем введения алгоритмической избыточности.

Пусть исходная система состоит из п последовательно соединенных элементов (рис. 5.6), вероятности отказа которых равны q1, q2, …, qn.

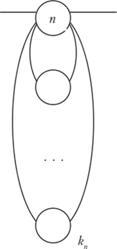
Рис. 5.6. Схема резервирования системы

К каждому из них с целью повышения надежности присоединим параллельно по ki штук резервных элементов. Каждый из полученных последовательных блоков имеет вероятность отказа 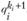, , 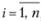так как весь блок откажет, если выйдут из строя все его элементы – и основной, и резервные. Следовательно, вероятность безотказной работы i-го блока равна 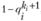, а всей резервированной системы:

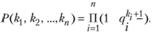(5.36)

При 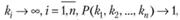неограниченным увеличением числа резервных элементов можно добиться сколь угодно высокой надежности. Однако ki, не могут быть произвольными. На их число накладываются ограничения, связанные с весом, объемом, стоимостью системы. Математически ограничения записываются в виде системы линейных неравенств

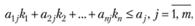(5.37)

где т – число ограничивающих условий. Задача нахождения

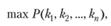(5.38)

при условиях (5.37) относится к задачам целочисленного программирования.

Отличие задач целочисленного программирования от задач нелинейного программирования состоит в том, что значения искомых переменных принимают только целые значения. Но это требует развития специальных методов исследования.