Методы информационного обеспечения решения некорректных задач
Рассмотрим строгое определение некорректно поставленных задач. Для этого воспользуемся также иллюстративными примерами 7.4-7.6, приведенными выше в параграфе 7.2.
Итак, необходимо решить операторное уравнение
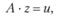(7.17)
где z – некоторый искомый элемент, который может быть вектором (в примере 7.4 это вектор параметров аj, а в примере 7.6 – вектор (а1, а2)), функцией (в примере 7.5 это V(t)), просто числом. Элементы-претенденты на решение сравниваются между собой в некотором пространств F с метрикой dF(z1;z2). Для примеров 7.4 и 7.6 таковой может быть, например, евклидова мера, для примера 7.5 – одна из мер сравнения функций между собой; и – известный элемент пространства U с заданной метрикой dN(u1,и2) (в примере 7.4 это вектор наблюденных значений временно́го ряда z(t), в примере 7.5 это функция (FT – FC), а в примере 7.6 – вектор (5; 7; 7)T); А – заданный оператор преобразования (матрица Ю. Уоккера в примере 7.4, дифференциальное уравнение (7.3) в примере 7.5 и матрица (7.6) в примере 7.6).
Задача определения решения z = R(u) операторного уравнения (7.17) называется устойчивой на паре метрических пространств (F; U), если для любого числа ε > 0 можно указать такое число σ(ε) > 0, что из неравенства du = (и1; и2) < σ(ε) следует dF = (z1; z2) < s, где z1 = R(u1), z2 = R(u2); u1, u2ÎU, z1, z2ÎF.
Различают корректно и некорректно поставленные задачи. Задача определения zÎF по заданным u Î U и А называется корректной, если:
• для всякого и Î U существует единственное решение z Î F,
• задача устойчива на пространствах F и U.
Задачи, в которых нарушается хотя бы одно из указанных требований, называются некорректно поставленными. Следует отметить, что задача, корректно поставленная на одной паре метрических пространств, может быть некорректной для другой.
Задача решения системы линейных алгебраических уравнений (7.6) является некорректной по первой причине: отсутствует набор значений а1 и а2, при которых удовлетворяются все уравнения системы (7.6). Это легко проверить, решая любую пару уравнений из системы (7.6) и подставляя полученное решение в третье уравнение.
Пример 7.9. Рассмотрим простой пример, в котором идентифицируется модель вида
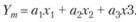(7.18)
Предположим вначале дополнительно, что входные переменные заданы без ошибки. Пусть также известно, что данные наблюдаются в точках, заданных табл. 7.6.
Несложный анализ позволяет сделать вывод, что данные табл. 7.6 не пригодны для постановки корректной математической задачи идентификации неизвестной зависимости. Действительно, все столбцы заданной матрицы являются взаимно зависимыми между собой: третий и пятый – это удвоенные первый и второй; четвертый и шестой – это суммы соответственно первого и второго и четвертого и пятого. То есть, если составить систему
линейных алгебраических уравнений, то она будет иметь множество решений. При трех неизвестных только два независимых соотношения в табл. 7.6.
Таблица 7.6
Данные для идентификации модели (7.18)
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
|
х1 |
5 |
3 |
10 |
8 |
6 |
14 |
|
х2 |
2 |
6 |
4 |
8 |
12 |
20 |
|
х3 |
1 |
3 |
2 |
4 |
6 |
10 |
|
Y |
4 |
7 |
8 |
11 |
14 |
25 |
Пример 7.10. Исследуется учебный процесс. Аргументами (управляемыми параметрами) являются длительность одного занятия т и частота занятий с. Выходными величинами будем рассматривать скорость усвоения материала V и объем полученных знаний Э.
Проведя ряд экспериментов, в результате которых табличным способом (аналогично табл. 7.6) фиксируются статистические зависимости между скоростью изменения уровня знаний V и аргументами с и τ, а также между объемом знаний Э и теми же аргументами с и т, проведя аналитические расчеты по методу наименьших квадратов, например, с помощью программного обеспечения MS Excel или иных программных продуктов, получим систему уравнений вида:
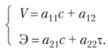(7.19), (7.20)
В матричном виде система этих уравнений представляется следующим образом:
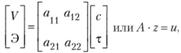(7.21)
где
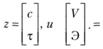
Уравнение (7.19) отражает зависимость скорости усвоения материала V от частоты и продолжительности его изучения сиτ, уравнение (7.20) выражает объем полученных при этом знаний Э от тех же переменных. Каждое уравнение имеет самостоятельное значение. Например, если известны, согласно расписанию занятий, значения с и τ, то можно рассчитать достигнутую скорость изучения и полученный объем знаний. Поставим задачу иначе: заданы необходимые скорость V и объем Э. Каковы должны быть с и τ, т.е. частота и продолжительность занятий, чтобы выполнить критериальные показатели?
Так как скорость приобретения знаний и их объем взаимосвязаны, уравнения в определенном смысле зависимы, что приводит к плохой обусловленности матрицы Л (близости к нулю ее определителя). Поэтому вычисление интересующих нас значений с и т по известным значениям V и Э с использованием обратного оператора А-1 может быть неустойчиво.
Приведем числовой пример аналогичной некорректно поставленной задачи. Пусть система алгебраических уравнений задается оператором
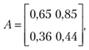
тогда
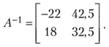
Результаты решения z = A-1 заданной системы уравнений при различных значениях V, Э (второй и третий столбцы) приведены в табл. 7.7 (четвертый и пятый столбцы).
Таблица 7.7
Исходные данные и результаты расчета управляющих воздействий
|
Номер наблюдения (вариант) |
V |
Э |
С |
τ |
cр |
τp |
|
1 |
2,35 |
1,24 |
1 |
2 |
1,5 |
1,6 |
|
2 |
2,39 |
1,24 |
0,12 |
2.72 |
0,9 |
1,8 |
|
3 |
2.4 |
1,2 |
–1,8 |
4,2 |
0,77 |
2,16 |
|
4 |
2,2 |
1,3 |
6,85 |
–2,65 |
0,69 |
0,39 |
Как очевидно из таблицы, малым отклонениям в значениях исходных данных (V, Э) соответствуют значительные отклонения в решении (с, τ). Решение для вариантов 3 и 4 вообще не имеет практического смысла, так как с и τ по смыслу задачи отрицательными быть не могут.
Приведенный пример показывает, что решение системы линейных уравнений не всегда непрерывно зависит от изменения исходных данных. На практике это может внести искажение в рассчитываемые решения, а иногда – даже привести к получению физически нереализуемых управлений.
Информационное обеспечение решения некорректных задач осуществляется на нескольких этапах:
• при сборе и отборе данных для построения моделей процессов и процедур принятия решений:
• в регуляризующих алгоритмах построения моделей;
• при регуляризации вычислительных алгоритмов.
Первый этап реализуется, в частности, процедурой активного эксперимента. Подробно этот этап описан в параграфе 7.2. Он характерен и при пассивном методе сбора информации. Здесь важно осуществить правильный отбор используемых данных.
Второй этап информационного обеспечения решения некорректных задач также достаточно полно представлен в параграфе 6.1. Более подробного рассмотрения требует третий этап: регуляризация вычислительных алгоритмов. Рассмотрим реализацию этого этапа на конкретных примерах.
Ниже приведены наиболее распространенные методы решения некорректных задач.
1. Метод подбора решения некорректно поставленной задачи.
Пример 7.11. Метод подбора решения – это широко распространенный метод приближенного решения некорректных задач. Он состоит в том, что априори заданы претенденты на решение г. Для каждого из них вычисляется оператор А • г, т.е. решается прямая задача. В качестве приближенного решения берется такой элемент г0, на котором невязка (рассогласование) du(A • z0; и) достигает минимума:
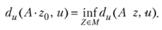(7.22)
Практически минимизация невязки du(A×z, и) производится приближенно, и возникает вопрос об эффективности метода подбора, т.е. о возможности как угодно приблизиться к искомому точному решению.
Возможность такой постановки хорошо иллюстрируется примером 7.10. Действительно, согласно существующим регламентам и учебным планам продолжительность занятий может быть или 2, или 4 академических часа в день, частота занятий – или один раз в 2 недели, или 1–2 раза в неделю. То есть количество вариантов решений, полученных комбинацией указанных значений, невелико, и решение легко поддается прямому перебору случаев.
Пример 7.12. Вернемся к модели (7.6) объекта, представленного на рис. 7.3.
Пусть заданы возможные претенденты на решение, т.е. пары значений искомых коэффициентов а, и а2: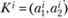 
. Вот эти значения:
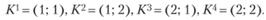
При подстановке в систему (7.6) значений а1 и а2 из Кi получаем невязки – рассогласования левых и правых частей системы уравнений (7.6). Для суммарной оценки невязок выберем обычную евклидову меру. Получим
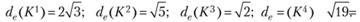
Минимальную невязку обеспечивает третий набор коэффициентов. То есть в качестве лучшего решения следует взять К3 = (2; 1). Иначе, а1 – 2 и а2 = 1.
2. Метод квазирешения.
Для решения некорректных задач при неточной правой части вводится понятие квазирешения.
Элемент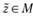 
, минимизирующий при данном и некоторый функционал du(A• z; и) на множестве М, называется квазирешением уравнения (7.17) на М, т.е.:
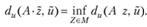(7.23)
Квазирешение может быть и не одно. В этом случае под ним будем понимать любой элемент из множества квазирешений D.
Пример 7.13. Воспользуемся условиями последнего решенного примера (система уравнений (7.6)). Будем считать значения а1 и а2 неизвестными. В качестве функционала регуляризации изберем обычную евклидову меру. Получим
(7.24)
Необходимо минимизировать соотношение (7.24).
Далее удобнее оперировать с 
. Дифференцируя последнее по а1 и а2 и приравнивая полученные производные к нулю, получим соответственно новую систему уравнений:
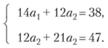
Откуда следует: а1 = 1,56 и а2 = 1,35.
3. Метод замены оператора.
Этот метод основан на замене исходного уравнения (7.17) близким ему, в некотором смысле, уравнением, для которого задача нахождения решения устойчива к малым изменениям правой части usU. В простейшем случае (метод М. М. Лавреньева) эта идея реализуется следующим образом.
Уравнение (7.17) заменяется уравнением
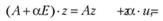(7.25)
где а > 0 – числовой параметр; Е – единичный оператор (в случае систем линейных алгебраических уравнений – единичная матрица). Решение уравнения (7.25)
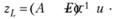(7.26)
при соответствующем выборе параметра а и принимается за приближенное решение уравнения (7.17).
Смысл данного подхода наиболее полно иллюстрируется на примере решения системы двух линейных уравнений с двумя неизвестными (7.21). Системы линейных уравнений имеют неустойчивые решения, если элементы строк матрицы А приближенно пропорциональны, т.е.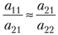 
. При точном равенстве система
или не имеет решения, или имеет бесконечное множество решений. Переход от (7.17) к (7.25) в данном случае приводит к соотношениям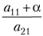 
и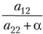 
, в которых изменяются одновременно и в одну сторону только крайние члены пропорции, что ведет к нарушению приближенного равенства и повышению устойчивости решения системы линейных уравнений.
Выбор значения параметра регуляризации а осуществляется через минимизацию специально подобранного регуляризующего оператора. Обоснование вида регуляризующего оператора, а затем и решение соответствующей задачи минимизации затруднительны в условиях нашей задачи. Открытыми остаются также следующие вопросы: почему изменяются только элементы главной диагонали? почему величина их изменения одинакова? Ответы на самом деле очевидны: так удобнее с вычислительной точки зрения. Принять этот ответ, не имеющий экономического и технологического обоснования, нельзя. В связи с этим предлагается получить "верхнюю" по устойчивости оценку решения. Далее предлагается усовершенствование метода, состоящее в следующем.
1. Изменяются все коэффициенты аij матрицы, т.е. вводится множество корректирующих параметров а".
2. Знак параметра выбирается из условия максимизации детерминанта (определителя) матрицы. Вопрос может быть решен использованием пробных шагов: сравнение двух значений определителя, которые получены при различных знаках исследуемого параметра.
3. Абсолютная величина поправочного коэффициента выбирается как наибольшее допустимое по ошибке идентификации коэффициента.
Вернемся к рассмотрению примера 7.10 с данными, заданными табл. 7.7. Пусть известно, что все коэффициенты матрицы А заданы с 5%-ной ошибкой. Кроме того, очевидно, что элементы главной диагонали для увеличения значения определителя матрицы следует изменять в направлении, противоположном изменению элементов второстепенной диагонали. Для исходной системы детерминант равен: -0,02. Поправочные коэффициенты, исходя из приведенных выше условий, будут равны:
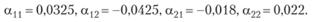
Новое значение матрицы имеет вид
Справка. Расчеты проводились до заданной точности с округлением по критерию снижения вероятности выхода за пределы допустимых норм. Теперь значение определителя равно –0,0778. Эффект метода на первом этапе процедуры очевиден. Как же изменилось решение при тех же исходных данных, которые заданы табл. 7.7 (столбцы 5 и 6)? Эго можно увидеть из ее последних столбцов (7 и 8). Эти решения обозначены соответственно ср и τр, что означает регуляризованное решение.
Физически нереализуемых (отрицательных) решений теперь уже нет, динамика изменения решений от одного случая наблюдения к другому случаю сопоставима с динамикой изменения коэффициентов матрицы. Увеличение порога варьирования коэффициентов матрицы (в примере он был равен 5%), если это позволяют условия задачи, позволит получить более устойчивое решение.