Коэффициенты прямых и полных материальных затрат

Переходя к анализу модели межотраслевого баланса, необходимо прежде всего рассмотреть основные свойства матрицы коэффициентов прямых материальных затрат А. Коэффициенты прямых затрат по определению являются неотрицательными, следовательно, матрица А в целом может быть названа неотрицательной: А > 0. Так как процесс воспроизводства нельзя было бы осуществлять, если бы для собственного воспроизводства в отрасли затрачивалось большее количество продукта, чем создавалось, то очевидно, что диагональные элементы матрицы А меньше единицы: aij < 1.

Система уравнений межотраслевого баланса является отражением реальных экономических процессов, в которых содержательный смысл могут иметь лишь неотрицательные значения валовых выпусков; таким образом, вектор валовой продукции состоит из неотрицательных компонентов и называется неотрицательным: X ≥ 0. Встает вопрос, при каких условиях экономическая система способна обеспечить положительный конечный выпуск по всем отраслям. Ответ на этот вопрос связан с понятием продуктивности матрицы коэффициентов прямых материальных затрат.

Будем называть неотрицательную матрицу А продуктивной, если существует такой неотрицательный вектор Х ≥ 0, что

Х > АХ (6.11)

Очевидно, что условие (6.11) означает существование положительного вектора конечной продукции Y > 0 для модели межотраслевого баланса (6.6).

Для того чтобы матрица коэффициентов прямых материальных затрат А была продуктивной, необходимо и достаточно чтобы выполнялось одно из перечисленных ниже условий:

1) матрица (Е - А) неотрицательно обратима, т.е. существует обратная матрица ;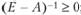

2) матричный ряд 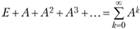сходится, причем его сумма равна обратной матрице ;

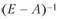3) наибольшее по модулю собственное значение l матрицы А, т.е. решение характеристического уравнения 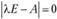, строго меньше единицы;

4) все главные миноры матрицы (Е - А), т.е. определители матриц, образованные элементами первых строк и первых столбцов этой матрицы, порядка от 1 до п, положительны.

Более простым, но только достаточным признаком продуктивности матрицы А является ограничение на величину ее нормы, т.е. на величину наибольшей из сумм элементов матрицы А в каждом столбце. Если норма матрицы А строго меньше единицы, то эта матрица продуктивна; повторим, что данное условие является только достаточным и матрица А может оказаться продуктивной и в случае, когда ее норма больше единицы.

Наибольший по модулю корень характеристического уравнения, приведенного в условии 3) продуктивности матрицы А (обозначим его через l*), может служить оценкой общего уровня коэффициентов прямых материальных затрат, а, следовательно, величина 1 - l* характеризует остаток после затрат, т.е. продуктивность. Чем больше 1 - l*, тем больше возможности достижения других целей, кроме текущего производственного потребления. Другими словами, чем выше общий уровень коэффициентов матрицы А, тем больше наибольшее по модулю собственное значение l* и ниже уровень продуктивности, и наоборот, чем ниже общий уровень коэффициентов матрицы А, тем меньше наибольшее по модулю собственное значение и выше продуктивность.

Перейдем к анализу матрицы коэффициентов полных материальных затрат, т.е. матрицы В = (Е - А)-1. Согласно определению 6.2 из предыдущего параграфа коэффициент этой матрицы показывает, сколько всего нужно произвести продукции i-й отрасли, чтобы получить единицу конечной продукции j-й отрасли.

Дадим другое определение коэффициента полных материальных затрат исходя из того, что кроме прямых затрат существуют косвенные затраты той или иной продукции при производстве продукции данной отрасли. Рассмотрим в качестве примера формирование затрат электроэнергии на выпуск стального проката, при этом ограничимся технологической цепочкой "руда - чугун - сталь - прокат". Затраты электроэнергии при получении проката из стали будут называться прямыми затратами, те же затраты при получении стали из чугуна будут называться косвенными затратами 1-го порядка, а затраты электроэнергии при получении чугуна из руды будут называться косвенными затратами электроэнергии на выпуск стального проката 2-го порядка и т.д. В связи со сказанным выше имеет место следующее определение.

Определение 6.3. Коэффициентом полных материальных затрат cij называется сумма прямых затрат и косвенных затрат продукции i-й отрасли для производства единицы продукции j-й отрасли через все промежуточные продукты на всех предшествующих стадиях производства. Если коэффициент косвенных материальных затрат k-го порядка обозначить через 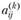, то имеет место формула

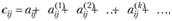(6.12)

а если ввести в рассмотрение матрицу коэффициентов полных материальных затрат С = (сij) и матрицы коэффициентов косвенных материальных затрат различных порядков 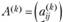, то поэлементную формулу (6.12) можно записать в более общем матричном виде:

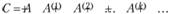(6.13)

Исходя из содержательного смысла коэффициентов косвенных материальных затрат можно записать ряд матричных соотношений:

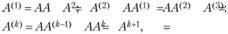
с использованием которых матричная формула (6.13) может быть переписана в следующем виде:

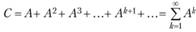(6.14)

Если матрица коэффициентов прямых материальных затрат А является продуктивной, то из условия 2) продуктивности существует матрица В = (Е - А)-1, являющаяся суммой сходящегося матричного ряда:

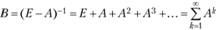(6.15)

Из сопоставления соотношений (6.14) и (6.15) устанавливается Вперед связь между двумя матрицами коэффициентов полных материальных затрат:

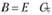
или, в поэлементной записи:

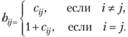
Данная связь определяет экономический смысл различия между коэффициентами матриц В и С: в отличие от коэффициентов матрицы С, учитывающих только затраты на производство продукции, коэффициенты матрицы В включают в себя кроме затрат также саму единицу конечной продукции, которая выходит за сферу производства.

Перейдем теперь к вычислительным аспектам решения задач на основе модели межотраслевого баланса. Основной объем расчетов по этой модели связан с вычислением матрицы коэффициентов полных материальных затрат В. Если матрица коэффициентов прямых материальных затрат А задана и является продуктивной, матрицу В можно находить либо по формулам обращения матриц, рассматриваемым в курсе матричной алгебры (некоторые из этих формул рассмотрены в гл. 2), либо приближенным способом, используя разложение в матричный ряд (6.15).

Рассмотрим первый способ нахождения матрицы В. Находят матрицу (Е - А), а затем, применяя один из прямых методов обращения невырожденных матриц, вычисляют матрицу (Е - А)-1. Одним из наиболее употребительных методов обращения матриц является метод Жордана. Часто применяется также метод, основанный на применении формулы матричной алгебры

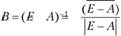(6.16)

где в числителе матрица, присоединенная к матрице (Е - А), элементы которой представляют собой алгебраические дополнения для элементов транспонированной матрицы (Е - А)', а в знаменателе - определитель матрицы (Е - А). Алгебраические дополнения в свою очередь для элемента с индексами i и j получаются умножением множителя (-1)i+j на минор, получаемый после вычеркивания из матрицы i-й строки и j-го столбца.

При втором способе вычисления матрицы коэффициентов полных материальных затрат используется формула (6.15). Обязательным условием корректности этих расчетов является условие продуктивности матрицы А, и при расчетах ограничиваются учетом косвенных материальных затрат до некоторого порядка включительно, например до 2-го, 3-го порядков. В этом способе используется процедура умножения квадратных матриц с их последующим сложением, и коэффициенты полных материальных затрат получаются с известным приближением (с недостатком).

Пример 6.1. Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат и вектор конечной продукции:

Найти коэффициенты полных материальных затрат и вектор валовой продукции, заполнить схему межотраслевого материального баланса.

1. Определим матрицу коэффициентов полных материальных затрат по второму (приближенному) способу, учитывая косвенные материальные затраты до 2-го порядка включительно. Запишем матрицу коэффициентов косвенных затрат 1-го порядка:

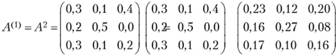
матрицу коэффициентов косвенных затрат 2-го порядка:

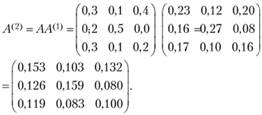
Таким образом, матрица коэффициентов полных материальных затрат приближенно равна

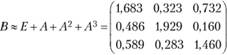
2. Определим матрицу коэффициентов полных материальных затрат с помощью формул обращения невырожденных матриц (первый способ):

а) находим матрицу (Е - А):

б) вычисляем определитель этой матрицы:

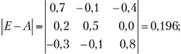
в) транспонируем матрицу (Е - А):

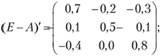
г) находим алгебраические дополнения для элементов матрицы

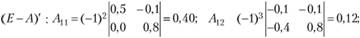
таким образом, присоединенная к матрице (Е - А) матрица имеет вид

д) используя формулу (6.16), находим матрицу коэффициентов полных материальных затрат:

Как отмечено выше, элементы матрицы В, рассчитанные но точным формулам обращения матриц, больше соответствующих элементов матрицы, рассчитанной по второму приближенному способу без учета косвенных материальных затрат порядка выше 2-го.

3. Найдем величины валовой продукции трех отраслей (вектор X), используя формулу (6.8'):

4. Для определения элементов первого квадранта материального межотраслевого баланса воспользуемся формулой, вытекающей из формулы (6.4): хij = aij Хj. Из этой формулы следует, что для получения первого столбца первого квадранта нужно элементы первого столбца заданной матрицы А умножить на величину X1 = 775,3; элементы второго столбца матрицы А умножить на X2 = 510,1; элементы третьего столбца матрицы А умножить на X, = 729,6.

Составляющие третьего квадранта (условно чистая продукция) находятся с учетом формулы (6.1) как разность между объемами валовой продукции и суммами элементов соответствующих столбцов найденного первого квадранта.

Четвертый квадрант в нашем примере состоит из одного показателя и служит, в частности, для контроля правильности расчета: сумма элементов второго квадранта должна в стоимостном материальном балансе совпадать с суммой элементов третьего квадранта. Результаты расчета представлены в табл. 6.2; незначительные расхождения по строкам таблицы объясняются погрешностью из-за округления чисел.

Таблица 6.2

Межотраслевой баланс производства и распределения продукции

Производящие отрасли

Потребляющие отрасли

Конечная продукция

Валовая продукция

1

2

3

1

232,6

51,0

291,8

200,0

775,3

2

155,1

255,0

0,0

100,0

510.1

3

232,6

51,0

145,9

300,0

729.6

Условно чистая продукция

155,0

153,1

291,9

600,0

Валовая продукция

775,3

510,1

729,6

2015,0