Измерение риска: распределение доходности отдельного актива

Допустим, в момент времени t = 0 цена некоторого актива равна 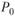(рис. 5.3). В момент времени I = 1 цена актива может стать 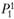, если ситуация будет развиваться чрезвычайно неудачно для актива. Также цена может стать 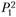, если ситуация будет развиваться лучше, чем для цены 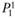Цена актива может и вовсе не поменяться или даже вырасти, например до уровня 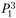, если ситуация будет развиваться благоприятным образом.

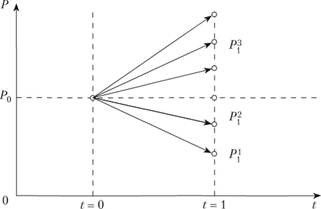
Рис. 5.3. Цена актива и ее изменение во времени

Каждое возможное развитие ситуации (i-е состояние мира) имеет некоторую вероятность своего наступления 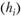, поэтому каждому значению цены актива 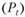в момент t при t-м состоянии мира можно поставить в соответствие вероятность. Это позволяет рассматривать цену (или доходность) актива как случайную величину, имеющую распределение и функцию плотности распределения.

На рис. 5.4 представлено два ожидаемых в момент t=0 распределения цены актива: одно – для момента t = 1, а другое – для момента t = 4. Очевидно, что с увеличением времени, прошедшего с момента инвестиции, на цену актива могут оказать влияние все больше и больше факторов, как благоприятных, так и наоборот. Все это приводит к тому, что функция плотности ожидаемого распределения "расползается" вдоль оси, увеличивая вероятности сильных изменений в цене актива. При этом среднее значение цены может оставаться неизменным, как это нарисовано на рис. 5.4, хотя и не обязательно.

На рис. 5.4 представлены распределения с симметричными функциями плотности, но вполне вероятны ситуации, когда функция плотности может быть скошена вправо (вероятность роста цены выше вероятности падения цены) или влево (вероятность роста цены меньше вероятности падения цены).

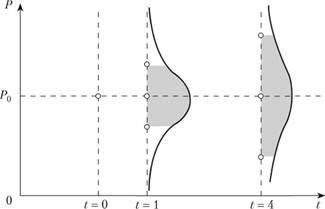
Рис. 5.4. Изменение цены актива во времени

Поскольку принятое ранее определение риска подразумевает, что отклонение в любую сторону – это плохо, то симметричные распределения подходят для использования. Отметим, что эмпирические исследования не всегда подтверждают симметричность распределений доходности активов на финансовых рынках, что заставляет исследователей искать меры риска для несимметричных распределений, например полудисперсию. Симметричные распределения очень удобны для анализа и построения моделей, поэтому финансовые исследования чаще основываются именно на подобных распределениях.

Функция плотности распределения полностью характеризуется первым и вторым моментами. Первый момент соответствует среднему значению величины, а второй – разбросу значений этого среднего, т.е. дисперсии.

Поскольку в каждом состоянии мира доходность актива может быть разной, то среднее значение рассчитывается как математическое ожидание и является ожидаемой доходностью актива:

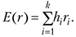(5.2)

Для измерения риска актива используют второй момент распределения – дисперсию, которая рассчитывается по формуле

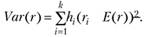(5.3)

Дисперсия подходит в качестве измерения риска, так как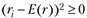 в формуле (5.3) и он будет увеличивать дисперсию при отклонении от ожидаемого результата в любую сторону. Это полностью согласуется с принятым определением риска, так как чем больше дисперсия актива, тем больше шансов, что реальное значение будет отличаться от ожидаемого, т.е. больше риск.

Также отметим одну особенность этих параметров распределения. Цена актива измеряется в рублях, первый момент распределения – ожидаемая цена – также измеряется в рублях, а вот второй момент распределения – дисперсия цены – измеряется в руб2. Что такое км2, понимают все, но что такое руб2, вряд ли кто-то сможет объяснить. Поэтому вместо дисперсии величины х чаще используют стандартное отклонение, которое является квадратным корнем из дисперсии, 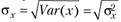. Стандартное отклонение имеет ту же размерность, что и исходная величина, что делает его использование более распространенным вследствие легкости интерпретации.

Пример 5.1. Имеются данные о следующих двух инвестиционных возможностях:

А		Б
Вероятность	Доходность, %	Вероятность	Доходность, %
0,10	0,10	0,15	0,08
0,20	0,12	0,15	0,10
0,30	0,15	0,15	0,18
0,40	0,20	0,55	0,24

Определите ожидаемую доходность, стандартное отклонение и коэффициент вариации (отношение стандартного отклонения актива к его доходности) для каждой альтернативы. Какое вложение представляется более рискованным? Какой из показателей – стандартное отклонение или коэффициент вариации – предпочтительнее использовать для сравнения риска различных альтернатив, подобных данным?

Решение

Для начала находим математическое ожидание доходности каждой альтернативы:

Для расчета дисперсии доходностей по альтернативам проще всего использовать запись, как представлена тут (это поможет избежать массы ошибок при расчетах):

Поскольку активы А и Б имеют разные значения и доходности, и стандартного отклонения, то целесообразней в качестве оценки риска использовать коэффициент вариации, показывающий величину риска на единицу доходности:

Таким образом, актив Б представляется менее рискованным.