Выявление тенденций с помощью локальных полиномиальных регрессий (LOESS)
Метод локальных полиномиальных регрессий (от англ. LOcal regrESSions – "LOESS" или LOcally WEighted Scatterplot Smoother – "LOWESS") разработал В. С. Кливленд в 1979 г.[1] Идея метода заключается в том, чтобы сгладить ряд значений, используя простую линейную либо полиномиальную зависимость у от х. Однако при этом предлагается строить модель не по всему ряду данных, а по его отдельным частям. Такой подход фактически позволяет построить простые регрессии для эволюционных рядов данных, так как при расчете коэффициентов используются лишь наиболее актуальные данные.
Рассмотрим метод локальных регрессий подробнее.
Идея метода заключается в том, чтобы рассчитать множество регрессий, центрами каждой из которых поочередно являются значения хi из ряда данных. При этом в расчете должны использоваться только некоторые точки хj находящиеся па заданном расстоянии от хi, такие, что
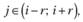(5.6)
где r – заданное исследователем натуральное число, рассчитываемое по формуле
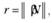
где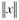 
обозначает округление числа х до целого по правилам математического округления; N – число наблюдений в выборке; 
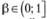– коэффициент сглаживания, по своему смыслу похожий на постоянную сглаживания в EWMA. Чем ближе β к 0, тем меньше значение r, тем меньше наблюдений включается в рассмотрение, а значит, сильнее учитываются точки, близкие к хi. При β = 1 получаем регрессию, построенную по всему ряду данных.
Каждому из значений, попавших в окно заданной ширины, задаются некоторые веса по принципу: чем дальше находится наблюдение от хi, тем меньше должен быть его вес. Например, на некоторой итерации рассчитывается регрессия с центром х41 и r = 4, т.е. в расчете регрессии так же используются значения х37, х38, х39, х40 и х42, х43, х44, х45. Веса у наблюдений ж37 и ж45 должны быть минимальными, в то время как вес центра наблюдения х41 – максимальным.
Возникает вопрос: как задать веса для этих наблюдений? Для этого вводится функция весов W(z), такая, что:
1) W(z) > 0, если |*|<1;
2) W(z) = 0, если |г|>1;
3) W(-z) = W(z);
4) W(z) не увеличивающаяся функция для |z| > 0.
Первое условие позволяет задать функцию и ограничить ее некоторым промежутком, второе – исключить из рассмотрения точки, выходящие за заданные границы, третье – задать одинаковые веса равноудаленным точкам слева и справа от центра. Последнее, четвертое, условие позволяет удаленным от центра точкам задать не больший вес, чем точкам, близким к центру.
Можно выбрать множество различных функций, удовлетворяющим данным условиям. Кливленд предложил для этого использовать биквадратную либо трикубическую функцию:
В данном случае z – это переменная расстояния, характеризующая удаленность наблюдений от центральной точки. В самой центральной точке z=0.
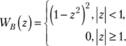(5.7)
и
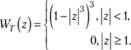(5.8)
На рис. 5.5 графически изображены биквадратная функция (5.7) и трикубическая функция (5.8).
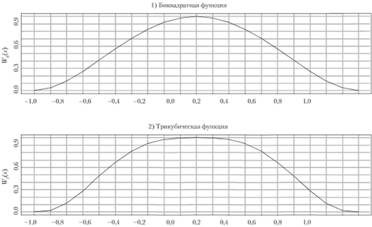
Рис. 5.5. Распределение весов по биквадратной (1) и трикубической (2) функциям в зависимости от значений z
Как видим, функция (5.7) предполагает более гладкое распределение весов, чем функция (5.8): значения, располагающиеся ближе к центру по биквадратной функции, имеют большие веса, чем по трикубической.
Стоит так же заметить, что сумма весов, распределенных по весовым функциям (5.7) и (5.8), не равна единице. Действительно, при построении LOESS несколько наблюдений могут оказаться на очень близком расстоянии от центральной точки, а значит, и веса у них будут близкими к единице. Очевидно, что сумма весов в таком случае будет больше единицы. Однако условие равенства суммы весов единице для построения LOESS не требуется, так как при расчетах коэффициентов локальных регрессий важно не то, какие именно веса имеют наблюдения, а то, как эти веса распределяются между ними.
После того как веса заданы, взвешенным методом наименьших квадратов рассчитываются оценки коэффициентов либо локально-линейной
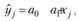(5.9)
либо локально-полиномиальной регрессии:
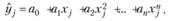(5.10)
Обычно для построения LOESS используются полиномы не выше второй степени, так как использование более высоких степеней сопряжено с вычислительными сложностями, сглаживание исходного ряда данных при этом осуществляется неэффективно, да и полученные при этом локальные регрессии не несут в себе какого бы то ни было смысла. К тому же известно, что полиномы высоких степеней дают неустойчивые прогнозные оценки.
После этого шага в распоряжении исследователя оказывается модель, па основе которой рассчитывается значение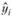 
при данном xi. Сама модель и ее коэффициенты обычно интереса не представляют, а вот расчетное значение 
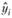сохраняется. Далее происходят переход к следующей точке, расчет весов, расчет коэффициентов новой модели и т.д. до тех пор, пока не будут получены 
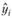для всех наблюдений, после чего в распоряжении исследователя оказывается сглаженный ряд 
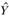, с которым далее уже можно работать.
Рассмотрим методику построения LOESS шаг за шагом. До начала построения LOESS исследователь задает коэффициент сглаживания β.
1. Выбирается i-е наблюдение. Очевидно, что на первом шаге i=1.
2. Для выбранной i-й точки рассчитывается расстояние hi от xi до наиболее удаленной от него точки, вошедшей в интервал (5.5):
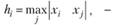(5.11)
где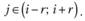 
Формула (5.11) позволяет выбрать максимальное из всех расстояний от центральной точки до точек, вошедших в интервал.
3. Рассчитываются веса для каждой j-й точки, попавшей в окно на основе выбранной весовой функции:
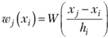(5.12)
На данном шаге обычно отдается предпочтение трикубической функции (5.8).
4. Рассчитываются коэффициенты выбранной модели (либо (5.9), либо (5.10)) взвешенным МПК:
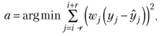[2](5.13)
5. В случае если исследователю нужны робастные оценки коэффициентов (оценки, устойчивые к выбросам), то осуществляется переход к шагу 6. Если же такие оценки не нужны, то происходит переход к первому шагу, выбирается следующее наблюдение.
6. По построенной на шаге 4 регрессии рассчитываются остатки: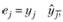 
по которым находится медиана: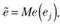 
На основе медианы рассчитывается медианное абсолютное отклонение:
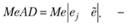(5.14)
Использование данной статистики обусловлено тем, что в случае несимметрично распределенных остатков, а также больших "выбросов", MeAD считается более адекватной и робастной оценкой, нежели, например, стандартное отклонение.
Кроме того, у этой величины есть полезное свойство, характеризующее связь MeAD со стандартным отклонением нормально распределенной величины, использующееся в статистике:
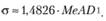(5.15)
7. После получения MeAD на предыдущем шаге на основе остатков рассчитываются новые (робастные) веса для каждого наблюдения:
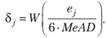(5.16)
В качестве весовой функции здесь обычно используется биквадратная функция (5.7).
У читателя может возникнуть правомерный вопрос: почему в знаменателе берется именно 6MeAD, а не какое-нибудь другое число. Из формулы (5.15) следует, что:
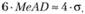
Использование такой величины позволяет убрать из рассмотрения все крайне редкие события, лежащие за пределами четырех стандартных отклонений (вероятность таких событий ниже 0,00004), которые можно классифицировать просто как "выбросы", искажающие картину мира.
Деление ошибок на 6MeAD приводит к тому, что в соответствии с формулами весовых функций наблюдения, лежащие близко к "выбросам", получают очень низкие веса, а наблюдения наиболее отдаленные от них – веса повыше.
8. После получения ряда новых весов рассчитываются новые коэффициенты выбранной модели (опять же либо (5.9), либо (5.10)) взвешенным МНК:
9. Шаги 6–8 повторяются т раз, после чего осуществляется переход к шагу 1, выбирается следующее наблюдение.
Обычная рекомендация по числу итераций т – это задать его равным 2, так как за две итерации обычно удается получить робастные оценки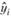 
[3].
На рис. 5.6 показан ряд данных № 1683 из базы рядов М3 (это ряд по отгрузке продукции), сглаженный LOESS (построенной средствами программы "R"[4]) с робастными оценками (т = 2) и разными коэффициентами сглаживания.
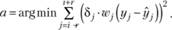(5.17)
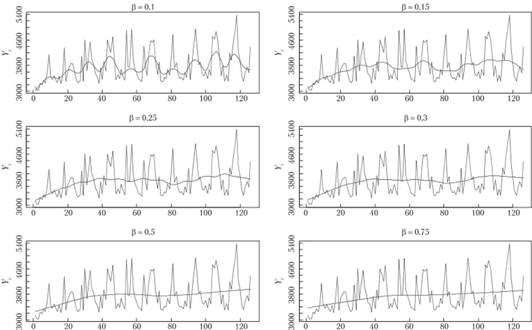
Рис. 5.6. Ряд данных № 1683 из базы М3 и его сглаживание с помощью LOESS с разными значениями коэффициента сглаживания
Как видим, при малых значениях β веса распределяются таким образом, что итоговые значения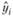 
сильнее реагируют на колебания в ряде данных и отклоняются от линии тренда. При β = 0,5 уже наблюдается достаточно плавная тенденция, по которой можно попробовать дать прогноз.
Как было замечено ранее, сами модели, коэффициенты которых рассчитываются на шаге 4 (или 8 – в случае с робастными оценками), в анализе и прогнозировании обычно не используются. Однако при прогнозировании эволюционных процессов можно прибегнуть к последним полученным оценкам и дать прогноз у для ожидаемого значения х – в оценке коэффициентов такой регрессии используются не все наблюдения, а только последние, поэтому и при прогнозировании будет использоваться только та часть ряда, которая характеризует последнее актуальное состояние объекта исследования. Нужно, однако, иметь в виду, что полученный в результате этого прогноз в большой степени будет зависеть от выбранного значения коэффициента сглаживания. Кроме того, в таком случае нужно четко понимать, какие части LOESS соответствуют последним наблюдениям.
Так, когда в качестве независимой переменной используется время (или номер наблюдения t), подобное упорядочение осуществляется автоматически. В результате этого можно взять модель, полученную на последнем наблюдении, и дать прогноз по намеченной тенденции. Например, для случая, показанного на рис. 5.6 по LOESS с β = 0,5, можно дать прогноз на несколько наблюдений вперед.
Если же мы рассматриваем зависимость у от некоторого х, определить последние наблюдения может быть крайне затруднительно, если вообще возможно.
Например, на рис. 5.7 показана точечная диаграмма по перевозке пассажиров на трамваях и численности населения с доходами ниже прожиточного минимума, а также эта зависимость, сглаженная LOESS.
Важная черта, которую можно отметить по этому графику, заключается в том, что зависимость между указанными факторами с течением времени изменилась, причем достаточно ощутимо. LOESS, сгладившая эту зависимость, прекрасно показала произошедшие трансформации. Однако прогноз по LOESS дать затруднительно: последние наблюдения на самом деле соответствуют точкам, лежащим в левом нижнем углу графика, что можно было бы выяснить, лишь проанализировав исходные данные.
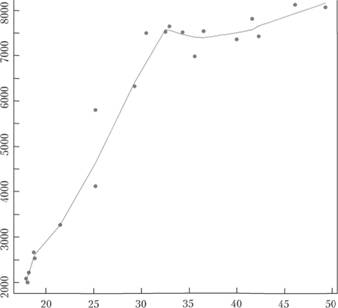
Рис. 5.7. Точечная диаграмма по перевозке пассажиров на трамваях (ось ординат), численности населения с доходами ниже прожиточного минимума (ось абсцисс) и сглаженная зависимость между этими факторами[5]