Вычисление оптимальных управлений и матричные уравнения Риккати

Рассмотрим применение уравнений Р. Беллмана для оптимизации линейных систем. Линейные уравнения динамики непрерывных и дискретных объектов имеют формы для:

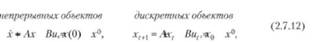
Пусть интегральные и суммарные функционалы, используемые для оптимизации систем управления, описываемых непрерывными и дискретными уравнениями типа (2.7.12), имеют вид

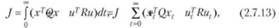
где О, = О/ £ О, Л = Лт > О — положительно определенные симметричные матрицы.

Предполагается, что объект вполне управляемый. Требуется вычислить управления с обратной связью, минимизирующие функционалы (2) на траекториях систем (1). Представим уравнения Беллмана для непрерывных и дискретных систем в соответствующих формах:

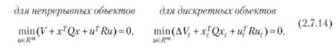
Выберем функции Ляпунова для непрерывных и дискретных объектов в виде соответствующих квадратичных форм:

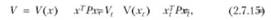
где Р = Рт > 0. Для преобразования необходимых условий (2.7.14) вычислим полную производную У(х) и приращение Д V, в силу дифференциальных и разностных уравнений (2.7.12).

Тогда можно получить два класса уравнений для непрерывных и дискретных систем, полученные вычислением полной производной или приращения функций Ляпунова в силу исследуемых систем. Получим для непрерывных и дискретных систем соответствующие полные производные и приращения, вычисленные в силу:

дифференциальных уравнений

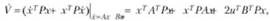
разностных уравнений

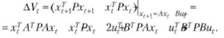
Далее необходимо подставить полную производную функции Ляпунова У(х) и приращение функции Ляпунова ДУ, в соответствующие дифференциальные и разностные уравнения Р. Беллмана как необходимые условия оптимальности.

В результате можно получить преобразованные уравнения Р. Беллмана рассматриваемых задач оптимизации в непрерывном и дискретном времени. Условия оптимальности, соответствующие непрерывному и дискретному времени, обладают специальной правой частью, представляющей собой конечномерную экстремальную задачу:

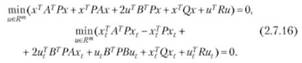
Вычислим минимум в левых частях полученных уравнений Беллмана для непрерывных и дискретных систем, используя правила векторного дифференцирования линейной и квадратичной форм вида: (стх)х=с,(хтМх)'х = 2Мх. Используя необходимое условие экстремума, можно получить линейные алгебраические уравнения для непрерывных и дискретных объектов:

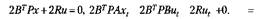
Тогда минимизирующие элементы и" и и" примут вид:

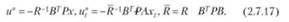
При подстановке управлений и* им,* в уравнения динамики непрерывных и дискретных объектов (2.7.16) можно получить уравнения для непрерывного (сверху) и дискретного (снизу)времени:

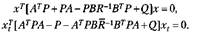
Для выполнения полученных равенств при любых векторах х и х, необходимо, чтобы были справедливы матричные уравнения

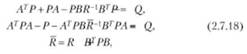
которые называются уравнениями Риккати. Уравнения сформулированы относительно матриц Р квадратичных функций Ляпунова для дифференциальных и разностных систем. Решения матричных нелинейных (квадратичных) алгебраических уравнений (2.7.18) не единственны. Необходимо с помощью численных методов найти решение, которое является положительно определенной матрицей. Условия существования таких решений определяются следующей теоремой.

Теорема 1.

Для существования единственного положительно определенного решения алгебраического уравнения Риккати достаточно выполнения условий:

1) пара матриц (Л, В) должна быть невырожденной, т.е. объект (2.7.12) с параметрами А, В — вполне управляемый (выполнен ранговый критерий управляемости Р. Калмана);

2) матрица Я > 0, т.е. положительно определенная;

3) требуется выполнение одного из двух условий:

а) матрица О_>0 — положительно определенная;

б) матрица ()> 0 и представима в виде 0_ = СТС, причем пара (А'г, С) — невырожденная.

Тогда оптимальные управления реализуются управлениями с обратной связью: и* - Кх, и* Кх,, параметры которых определяются уравнениями (2.7.18) так, что:

Приведенные результаты являются решением задачи оптимальной стабилизации и основой синтеза оптимальных систем.

Таким образом, описанные методы оптимизации систем управления позволяют синтезировать оптимальные управления и сформировать опенки качества управления на основе единой методики для линейных непрерывных и дискретных объектов, что подтверждается общностью операций, необходимых для решения задачи. Эти оценки могут быть также использованы при принятии решений в условиях неполной информации, которая не может быть учтена формализованными математическими средствами, а требует обработки экспертных оценок для различных условий и вариантов.