Выбор рискового портфеля и диверсификация

Очень часто индивид осуществляет выбор не только между безрисковым и рисковым активом, но и между различными видами рисковых активов, составляя оптимальный для себя портфель вложений.

Поскольку в портфель рисковых активов входят ценные бумаги и другие вложения разного рода, возможно возникновение взаимного влияния активов друг на друга.

Оценка риска взаимодействия двух случайных величин хиу производится по методу стохастической зависимости. Пусть qi■ — вероятность того, что переменная у примет значение тогда, когда переменная х примет значение х{. Характер зависимости двух случайных переменных отражается в матрице вероятностей (табл. 8.1)

Таблица 8.1. Матрица вероятностей при стохастической зависимости двух величин

В портфельном анализе используют две количественные меры взаимозависимости двух случайных переменных. Ковариация:

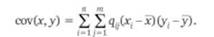
Коэффициент корреляции:

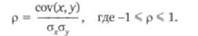
Ковариация показывает, насколько две случайные переменные, например, такие как доходности двух ценных бумаг, зависят друг от друга. Если ковариация положительна, это означает, что доходности (или цены) двух ценных бумаг имеют тенденцию изменяться в одном направлении, так что, к примеру, рост доходности или цены одной из бумаг скорее всего повлечет за собой увеличение доходности или цены другой ценной бумаги. Отрицательная ковариация демонстрирует противоположную зависимость между показателями двух ценных бумаг. Рост цены одной ценной бумаги будет, вероятно, сопровождаться падением цены или доходности другой ценной бумаги. Если значение ковариации приближается к нулю или равно ему, то связь между параметрами ценных бумаг отсутствует либо очень слаба.

Коэффициент корреляции используется для облегчения сравнения динамики случайных переменных с другими парами, поскольку нормирует ковариацию. Если р = -1, между переменными наблюдается полная отрицательная корреляция. Если р = 1 — наблюдается полная положительная корреляция. При р = 0 связь между переменными отсутствует.

Как же составить оптимальный портфель из нескольких рисковых активов?

Предположим, индивид хочет распределить свои средства между двумя видами ценных бумаг — акциями компании А и акциями компании Б. Известны показатели риска и доходности для этих ценных бумаг — (аА, гА) и (аБ, гн) соответственно. Пусть а —доля акций компании А в портфеле индивида (инвестора). Тогда средняя доходность портфеля будет г = схГд + (1 - а)гБ. Это ожидаемая доходность портфеля вложений.

Риск портфеля находится по формуле, определяющей дисперсию суммы двух случайных переменных:

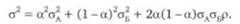
Если ожидаемая доходность инвестиционного портфеля представляет собой средневзвешенную из средних доходностей ценных бумаг, где в качестве весов используются доли активов во вложении, то риск комплексных вложений является более сложным по своей природе. В зависимости от корреляции доходности активов между собой, т.е. в зависимости от характера взаимосвязи динамики ценных бумаг, риск портфеля может как уменьшаться, так и увеличиваться по сравнению с суммой рисков отдельных вложений самих по себе.

Дисперсия суммы двух случайных величин

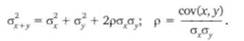
Дисперсия суммы произведения двух случайных величин на константы

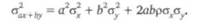
Рассмотрим частный случай.

Пусть Гд = гев = ге и Од = о2в = а2 — доходности и риски ценных бумаг одинаковы. Предположим, индивид вкладывает одну половину своих средств в акции компании А, а другую — в акции компании Б: а = 1/2. Доходность портфеля будет равна средней доходности любой из ценных бумаг.

Риск портфеля составит

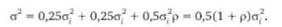
Если р = 0 — бумаги не связаны друг с другом, не коррелируют друг с другом, т.е. о2 = 0,5а2 — дисперсия портфеля оказывается равной только половине дисперсии каждого из вложений по отдельности.

Если р = -1, то а2 = 0 — у портфеля активов риск отсутствует, т.е. он безрисковый.

Если р = 1, то а = а(- — риск портфеля равен риску одной из ценных бумаг. Это максимальный риск для данного случая.

Таким образом, правильная диверсификация портфеля уменьшает совокупный риск. Дисперсия портфеля вложений меньше (или в крайнем случае не больше) средневзвешенной суммы дисперсий входящих в него активов.

Зная, как связаны между собой дисперсия портфеля вложений и доля, приходящаяся на одну ценную бумагу, можно найти оптимальную а*, при которой риск портфеля минимальный. Для этого вычислим условие первого порядка: с?о (а)/йа = 0. Откуда получаем

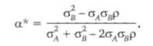
Найдем оптимальные доли акций при разных значениях коэффициента корреляции.

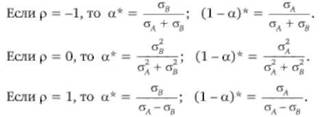
В каждом из этих случаев при соблюдении оптимальных долей индивид получает безрисковый портфель а2 = 0.

Обратим внимание на последний случай. Когда доходности ценных бумаг положительно коррелируют между собой, то

1) если ав > Од, (1 - а) < 0 или

2) если ав < аЛ, а < 0.

Это означает, что в оптимальном портфеле доля одной из акций должна быть меньше нуля — индивид должен продавать ценные бумаги "без покрытия", не имея их в наличии. Данная ситуация носит название короткие продажи.

Однако не всем индивидам нужен минимальный риск портфеля. Некоторые инвесторы согласны на высокий риск, если им предложат портфель с более высокой ожидаемой доходностью.

Выразим из уравнения

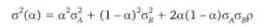
значение доли а как функции от рисков ценных бумаг и портфеля в целом а = а(ад, ав, а ). Подставим это значение в уравнение средней доходности портфеля г = агд + (1 - а)гв. В результате получим функциональную зависимость между доходностью и риском портфеля, в зависимости от коэффициента корреляции ге =/(а2, р). Рисунок 8.2 демонстрирует эту зависимость при разных р.

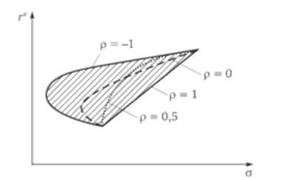
Рис. 8.2. Эффективное множество портфелей

Так как коэффициент корреляции -1 < р < 1, линия зависимости между риском и доходностью портфеля вложений очерчивает эффективное множество возможных портфелей для инвестирования. Эффективное множество обладает двумя характеристиками. Любой портфель из этого множества: 1) обеспечивает максимальную ожидаемую доходность для некоторого уровня риска; 2) обеспечивает минимальный риск для некоторого значения ожидаемой доходности. Эффективное множество представлено заштрихованной областью на рис. 8.2.

Портфели, расположенные за границами эффективного множества, не являются эффективными и никогда не будут выбраны инвестором.

Граница эффективного множества показывает линию бюджетного ограничения для индивида, выбирающего оптимальный портфель вложений.

Предпочтения индивида относительно риска и доходности и здесь могут быть представлены в виде функции полезности. Примером подобной функции может служить функция Рубинштейна и = Ч*ге - а2, где ¥ — индивидуальные предпочтения инвестора относительно доходности и риска. В качестве параметра 4* можно использовать, например, индекс Пратта — Эрроу, известный из микроэкономики.

Выразив значение доходности портфеля через переменную риска (дисперсию портфеля), получаем кривые безразличия с положительным наклоном

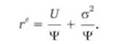
Теперь с помощью обычных методов оптимизации можно найти максимальную полезность при ограничении, описываемом границей эффективного множества. Поскольку для индивида, не склонного к риску, кривые безразличия выпуклы и имеют положительный на-

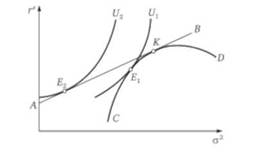
Рис. 8.3. Оптимальный выбор инвестором портфеля рисковых активов

клон, а граница эффективного множества вогнута, это решение будет единственным. Рисунок 8.3 показывает равновесие для инвестора при выборе только рисковых активов и при наличии безрисковой альтернативы.

Если индивиду предлагаются только рисковые активы, то линия СО характеризует границу эффективного множества портфелей. Оптимум инвестора находится в точке точке касания линии СО и кривой безразличия (/,. При включении одного безрискового актива индивид будет ориентироваться на линию АВ, показывающую теперь его бюджетное ограничение (как в модели Марковича, проанализированной ранее). Так как выбор осуществляется на основе одинакового набора рисковых вложений, к которым только добавляется один безрисковый актив, линия АВ должна касаться линии СО — на рисунке это точка К. Точка К никогда не будет выбрана, поскольку характеризует портфель с более высоким риском, чем набор в точке Еу Это иллюстрирует тот факт, что точка К расположена на менее предпочитаемой кривой безразличия.

Будет ли выбран портфель с безрисковым активом, если имеются портфели только с рисковыми активами? Для индивида, не склонного к риску, кривая безразличия, соответствующая выбору портфеля с безрисковым активом, расположена левее и выше, чем выбор исключительно рискованного набора. Оптимум в данном случае будет находиться в точке Е2, соответствующей кривой безразличия и2. А так как и2 > 17,, портфель Е2 окажется для инвестора предпочтительнее портфеля Ег.