Дисперсия и ее оценка

И снова вернемся к опыту с бросанием монеты.

Бросив монету десять раз, вполне вероятно получить результат, когда "орел" не выпадет ни разу. В 100 испытаниях нулевой результат значительно менее вероятен. Еще менее вероятен он в 1000 или 1 млн испытаний. Скорее всего, если мы имеем дело с действительно нормальной монетой, проведя большое число испытаний, включающее по 100 бросаний каждое, можно обнаружить, что число выпадений "орла" колеблется где-то около 50.

Параметр, который отражает теоретически ожидаемое отклонение случайной величины от ее математического ожидания, называется дисперсией.

В математической статистике дисперсия определяется как центральный момент второго порядка. Обозначим математическое ожидание случайной величины х как М(х), а дисперсию как D(x). Тогда формально дисперсия может быть определена следующим образом:

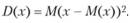
Иными словами, дисперсию можно определить как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Пользуясь этим определением, можно попытаться найти оценку для дисперсии (обозначим ее как s2), используя среднее арифметическое в качестве оценки такого математического ожидания. Очевидно, что это можно сделать следующим образом:

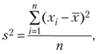(1.3)

где xi – наблюдаемые значения интересующей нас случайной переменной; п – объем выборки, т.е. число собранных эмпирических значений; 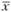– оценка для математического ожидания (среднее арифметическое по выборке), может быть получена по формуле (1.2).

Однако, как оказывается, если оценка математического ожидания, проведенная по формуле (1.2), является несмещенной, т.е. ее ожидаемое значение как раз равняется величине математического ожидания, то оценка дисперсии, выполненная по формуле (1.3), таковой не является. Оценка дисперсии, проведенная по формуле (1.3), является на самом деле выборочной, но не популяционной. Иными словами, эта оценка характеризует величину дис-

Персии только для данной выборки, но не для всей популяции данных (генеральной совокупности). И это вполне понятно – ведь сравнение значений случайной величины осуществляется не относительно истинного значения математического ожидания, как это предполагает само определение дисперсии, а лишь относительно его более или менее точной, пусть и несмещенной, оценки. Обычно в эксперименте бывает важным оценить именно популяционные характеристики математического ожидания и дисперсии.

Таким образом, вследствие того, что процедура, задаваемая по формуле (1.3), предполагает сравнение эмпирических значений х не с истинной величиной математического ожидания μ (которая практически никогда не бывает известна – ведь это лишь теоретическая величина), а только с ее оценочной характеристикой, происходит смещение оценки дисперсии. Методами дифференциального исчисления установлено, что ожидаемая величина оценочного значения дисперсии, рассчитанной по формуле (1.3), описывается следующим соотношением:

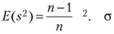(1.4)

Таким образом, получается, что если у нас есть десять выборочных значений какой-либо случайной величины, то, как показывает уравнение (1.4), оценивая дисперсию по формуле (1.3), мы занижаем ее значение, получая лишь 9/10 дисперсии исследуемой величины для генеральной совокупности. Увеличив объем выборки в десять раз, мы сможет уменьшить величину смещения до одной сотой, но все равно полученная величина будет отличаться от ожидаемого значения дисперсии. Однако, руководствуясь формулой (1.4), несложно найти способ расчета несмещенной оценки дисперсии:

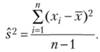(1.5)

Оценка дисперсии, представленная формулой (1.5), называется популяционной дисперсией, или дисперсией для генеральной совокупности, тогда как оценка дисперсии, полученная по формуле (1.3), называется выборочной. Таким образом, если мы хотим оценить этот параметр распределения случайной величины в какой-либо генеральной совокупности, мы должны воспользоваться формулой (1.5), тогда как формула (1.3) может быть использована, когда требуется лишь определить степень вариативности данных внутри выборки и выход за пределы имеющихся значений не предполагается даже в теории.

Иногда бывает важным оценить не столько дисперсию случайной величины, т.е. величину σ2, сколько саму σ. Этот параметр принято называть стандартным отклонением. Поскольку величины дисперсии и стандартного отклонения связаны взаимно однозначным соотношением, не существует особой проблемы для оценки стандартного отклонения. Аналогично оценке дисперсии оценка стандартного отклонения может проводиться как для выборки, так и для генеральной совокупности. На практике оценка стандартного отклонения может быть и, как правило, является предпочтительной, так как эта величина характеризуется меньшей размерностью и, следовательно, более удобна для восприятия. Кроме того, стандартное отклонение используется при вычислении стандартной ошибки измерения (SE):

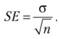
Эта статистика оказывается, в частности, необходимой для интервальной оценки исследуемой случайной величины. Подробнее об этом будет сказано в гл. 2.

Другим способом оценки вариативности в распределении случайной величины является оценка полумежквартильного интервала (Q). Эта величина в ряде случаев используется в качестве альтернативы стандартного отклонения, хотя и связана с ним однозначным соотношением Q = 0,67σ.

Как указывалось выше, квартилем называют еще один вариант квантиля распределения. Если медиана соответствует половине распределения, то квартиль – его четверти. Первая четверть распределения называется первым квартилем, второй квартиль это половина распределения (или медиана), третий квартиль – 3/4 распределения, наконец, четвертый квартиль соответствует всему распределению случайной величины. Полумежквартильный интервал соответствует половине значения разницы между первым и третьим квартилем распределения:

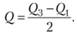
Оценка полумежквартильного интервала в качестве величины вариативности случайной величины используется, например, в сенсорной психофизике при оценке порога методом констант (Ч. А. Измайлов, М. Б. Михайловская [9]).

Надо отметить также, что в ряде случаев бывает важным оценить дисперсию не одной, а одновременно двух случайных величин х и у. Для этого можно использовать следующую формулу:

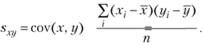
Полученная таким образом статистика называется ковариацией х и у. Она отражает степень связи этих двух переменных. В отличие от дисперсии и стандартного отклонения, которые не могут выражаться отрицательными числами, ковариация может принимать любые значения. Поскольку величина ковариации зависит в значительной степени от размерности самих величин, между которыми устанавливается связь, то по ее величине оценить степень связи между этими переменными не представляется возможным. Поэтому в качестве меры связи двух переменных принято использовать не ковариацию, а параметр, производный от нее, – корреляцию. Величина корреляции может быть получена в результате деления ковариации па произведение стандартных отклонений двух случайных величин, между которыми вычисляется ковариация. Иными словами, корреляция определяет степень ковариации случайных величин, распределенных в соответствии с законом стандартного нормального распределения. Более детально о разных видах корреляции и ковариации мы поговорим в гл. 7–9.