Теория игр

Теория игр – математический метод изучения оптимальных стратегий в играх. Под игрой понимается процесс, в котором участвуют два и более лица, ведущих борьбу за реализацию своих интересов. Лица, участвующие в игре, называются игроками. Если в игре участвуют две стороны, то ее называют игрой двух лиц. Если число сторон больше двух, ее относят к игре п игроков. Решения, которые принимают игроки, называются стратегиями. Под стратегией понимают возможные действия, позволяющие игроку на каждом этапе игры выбирать из определенного количества альтернативных вариантов такой ход, который представляется ему лучшим ответом на действия других игроков. По количеству стратегий игры делятся на конечные и бесконечные. В конечной игре каждый из игроков имеет конечное число возможных стратегий. Если хотя бы один из игроков имеет бесконечное число возможных стратегий, игра является бесконечной. Результатом игры является выигрыш или проигрыш (что может отражать прибыль или убыток предприятия). Различают игры с нулевой и с ненулевой суммой. Игра с нулевой суммой (антагонистическая игра) реализуется тогда, когда сумма выигрышей всех игроков в каждой партии равна нулю. Игра, в которой нужно вносить взнос за право участия в ней, является игрой с ненулевой суммой.

Большое значение в теории игр отводится равновесию. Ситуация называется равновесной, если ни один из игроков не заинтересован в том, чтобы ее нарушить. В случае антагонистической игры ситуация равновесия называется седловой точкой. Функция выигрыша игры во всех ее седловых точках принимает одно и то же значение, которое называется ценой игры. Именно ситуации равновесия могут быть предметом договоренности между игроками.

Возможные варианты игры сводятся в платежную матрицу, в которой строки соответствуют различным стратегиям игрока А, столбцы – стратегиям игрока В. В общем виде матричная игра может быть записана следующей платежной матрицей:

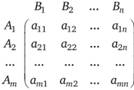
где А; – стратегия первого игрока;

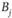– стратегия второго игрока;

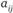– значения выигрыша первого игрока при выборе им i-й стратегии, а вторым игроком j-й стратегии.

Поскольку данная игра является игрой с нулевой суммой, значение выигрыша для второго игрока является величиной, противоположной по знаку значению выигрыша первого игрока.

Каждый из игроков стремится максимизировать свой выигрыш с учетом поведения противодействующего ему игрока. Поэтому для первого игрока необходимо определить минимальные значения выигрышей в каждой из стратегий, а затем найти максимум из этих значений, т.е. определить величину

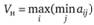
или найти минимальные значения по каждой из строк платёжной матрицы, а затем определить максимальное из этих значений. Величина 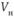называется максимином матрицы или нижней ценой игры.

Величина выигрыша первого игрока равна, по определению матричной игры, величине проигрыша второго игрока. Поэтому для второго игрока необходимо определить значение

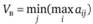
или найти максимальные значения по каждому из столбцов платёжной матрицы, а затем определить минимальное из этих значений. Величина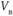называется минимаксом матрицы или верхней ценой игры.

В случае равенства 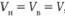, игра имеет решение в чистых стратегиях, а стратегии, в которых достигается V – оптимальными чистыми стратегиями. Величина V называется чистой ценой игры.

Пример

Предприятие имеет возможность выпускать три вида продукции в течение определенного периода времени. Другое предприятие (конкурент) в данном периоде также имеет возможность выпускать три аналогичных вида продукции. Результаты возможных событий представлены в платежной матрице:

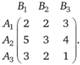
Определим верхнюю и нижнюю цену игры:

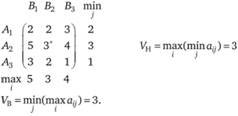
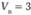Если игрок А будет постоянно придерживаться стратегии А2 то будет иметь гарантированный выигрыш . В этих условиях игроку В следует придерживаться стратегии В2, при которой он меньше всего проиграет, . Таким образом пара стратегий 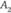, составят решение игры, цена которой будет равна 3. Данный элемент называется седловой точкой матрицы (в матрице выделен звездочкой). Это характеризует, что игра имеет решение в чистых стратегиях.

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. В этом случае можно получить оптимальное решение с использованием смешанных стратегий. Представим следующую платежную матрицу:

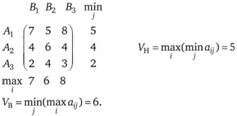
Поскольку минимакс и максимин в матрице не совпадают, следовательно, равновесия в чистых стратегиях не существует и для решения игры необходимо использовать смешанные стратегии. Определение пары смешанных стратегий приводит к тому, что если один из игроков придерживается свой оптимальной стратегии, то другому игроку невыгодно отступать от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры V, которая должна удовлетворять неравенству 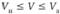. Нахождение такого решения сводится к решению прямой и двойственной задачи линейного программирования.

Выполним подстановку задачи. Найдем смешанные стратегии для игроков А и В:

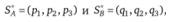
где р и q – вероятности применения соответствующих чистых стратегий игроками А и В.

По условию задачи выигрыш каждого игрока не может быть меньше цены игры V. Поэтому данная задача может быть представлена для игроков в виде следующих систем линейных неравенств:

Чтобы определить значение цены игры, надо обе части каждого из уравнений разделить на V. Введем обозначения 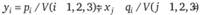и составим две задачи линейного программирования:

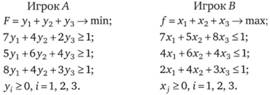
В результате решения задач в Excel получаем следующие результаты:

Интерпретируем результаты расчетов. Значение целевой функции F = 0,1818, отсюда 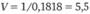(цена игры). При этом 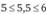Для определения значений вероятностей выбора смешанной стратегии игрока А умножим значения переменных на V:

Соответственно вероятность выбора смешанной стратегии игроком В:

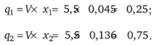
Следовательно, для достижения своей оптимальной стратегии игрок А с вероятностью 0,5 должен производить продукцию 1 и с вероятностью 0,5 – продукцию 2. В свою очередь, игрок В должен с вероятностью 0,25 сосредоточиться на выпуске продукции 1 и с вероятностью 0,75 – на выпуске продукции 2. Продукцию 3 не рекомендуется выпускать обоим игрокам.