Теорема о медианном избирателе и многомерные альтернативы

В конце 1940-х гг. Дункан Блэк обнаружил достаточное (но не необходимое) условие достижения устойчивого равновесия в коллективном выборе. Если индивидуальные предпочтения являются одновершинными, то устойчивую коллективную поддержку получает альтернатива, наиболее предпочитаемая медианным избирателем.

Понятия одновершинного предпочтения и медианного избирателя интуитивно легко воспринимаются с помощью рис. 4.2. На этом рисунке Q – количество некоего общественного блага, U – значения функций индивидуальной полезности участников голосования, отвечающие тому или иному уровню производства этого блага. Соизмеримость этих значений для разных индивидов не предполагается, поэтому существенно лишь, что соответствующие функции достигают максимума при разных величинах Q. Буквами V1, V2, V3, V4, V5 обозначены графики зависимостей U ot Q для пяти голосующих.

V1, V2, V3, V4, V5 обозначены графики зависимостей U от Q для пяти голосующих.

Графики одновершинны, т.е. мера удовлетворенности каждого из голосующих сначала монотонно возрастает с увеличением Q, а потом, достигнув максимума, начинает так же монотонно убывать. Третьего голосующего можно считать медианным в том смысле, что по обе стороны его точки максимальной удовлетворенности Q3 находятся по две точки максимальной удовлетворенности других участников выбора. Очевидно, третий голосующий способен кооперироваться с первым и вторым против четвертого и пятого, либо с четвертым и пятым – против первого и второго.

Обратим внимание, что все альтернативы, между которыми делается выбор, расположены в данном случае на одной шкале Q, что, собственно, и придает ясный смысл понятию медианного участника

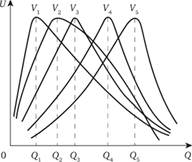
Рис. 4.2. Одновершинные предпочтения избирателей

выбора (избирателя). Подобные шкалы могут фиксировать меру не только объема производства общественного блага, но и, например, величины налога и других переменных, по поводу которых принимаются коллективные решения.

Теперь дадим более строгие определения и докажем теорему о медианном избирателе. Пусть функция полезности i-го индивида 17. определена на множестве значений некоей переменной х. Наиболее предпочитаемое данным индивидом значение рассматриваемой переменной 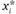назовем идеальной точкой. Это значит, что для всех х, неравных 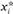, по определению, .

Пусть у и z – две точки на шкале значений х, таких, что либо и у, и z меньше или равно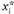, либо и у, и z больше или равно 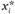. Предпочтения i-го голосующего называются одновершинными в том и только том случае, если при всегда , и наоборот.

Пусть – идеальные точки η голосующих индивидов. Обозначим 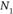– число идеальных точек, таких, что 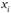меньше или равно некоторому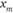, а 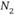– число идеальных точек 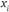, таких, что 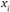больше или равно 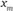. Точка 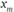называется медианной позицией тогда и только тогда, когда 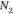и , и 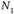больше или равно (N/2).

Теорема о медианном избирателе формулируется следующим образом: если х –множество альтернатив, расположенных на одной шкале, всем участникам выбора свойственны одновершинные предпочтения, определенные на х, и выбор совершается на основе правила простого большинства, то медианная позиция не может проиграть.

Предположим, что какой-либо из допустимых вариантов 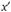побеждает 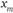. Пусть 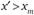. Тогда по крайней мере для голосующих альтернатива 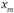предпочтительнее, чем 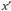. В самом деле, 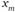ближе к идеальным точкам этих голосующих, чем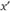, а такая близость по определению одновершинного предпочтения дает преимущество. Между тем по определению медианной позиции 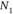составляет не меньше половины голосующих. Следовательно, вариант 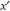не способен завоевать поддержку большинства. Аналогично доказывается невозможность забаллотировать вариант 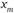при .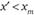

Если альтернативы, по отношению к которым совершается коллективный выбор, можно расположить на одной шкале, то весьма вероятно, что предпочтения голосующих будут одновершинными. Людям обычно свойственно выше оценивать такие варианты решений, которые ближе к наиболее предпочитаемым ими состояниям, по сравнению с вариантами, которые дальше от идеала. Если кто-то считает оптимальным расходовать на развитие культуры 2% бюджета, то скорее всего для него 1,5%-ные затраты привлекательнее 1%-ных, а 3%-ные – 4%-ных.

Однако всегда ли оцениваемые альтернативы удается разместить на одной шкале? Часто встречаются решения, которые по природе своей многомерны. Достаточно типичен, например, случай, когда одновременно приходится принимать взаимосвязанные решения о том, какие количества нескольких разных общественных благ произвести и какими должны быть размеры налогов. Впрочем, и при наличии многомерного выбора предпочтения голосующих иногда складываются таким образом, что представление о медианном участнике выбора остается в силе.

Если решаемая проблема имеет, например, два измерения, то предпочтения удобно графически изображать так, как это сделано на рис. 4.3.

Пусть 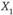и 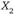– две самостоятельные характеристики рассматриваемых альтернатив (это могут быть, скажем, количества двух разных видов общественных благ, которые предстоит произвести при данном объеме бюджетных ассигнований). Для индивида А наиболее предпочтительно такое сочетание 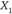и 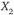, которое фиксируется на графике точкой А, а для индивида В – сочетание, фиксированное точкой В. Представим себе, что имеется третья ось координат U, перпендикулярная к плоскости, на которой расположены ос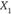и и 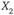; по этой третьей оси откладываются значения полезности всевозможных сочетаний альтернатив для индивидов.

Замкнутые кривые 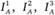и т.д. соединяют точки, соответствующие альтернативам, равноценным для первого индивида, а кривые

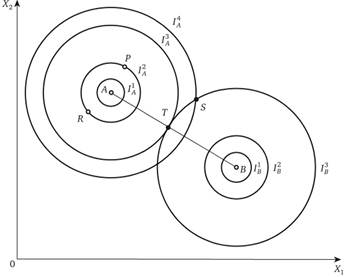
Рис. 4.3. Двумерные предпочтения двух индивидов

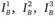и т.д. – соответствующие альтернативам, равноценным с позиций второго индивида (например, для индивида А равноприемлемы точки Р и R). Одновершинные кривые, изображенные на рис. 4.2, можно сопоставить с конусами, чьи проекции вершин и линий одного уровня изображены на рис. 4.3.

Если в выборе участвуют два индивида (или две группы лиц с тождественными предпочтениями), то будет избран вариант, соответствующий какой-либо точке касания лини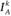й и 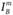(k и m – любые). В самом деле, если бы решение соответствовало точке, в которой касание таких линий не происходит, например точке S, то, переместившись по замкнутой кривой в точку касания Т, можно было бы, не ухудшив положение избирателя (или группы избирателей) В, улучшить положение А. В отношении же точек касания очевидно, что каждой из них соответствует Парето-эффективное состояние. Эти точки в совокупности составляют контрактную линию, изображенную на рис. 4.3 отрезком АВ.

Допустим, что в выборе участвуют не два, а три индивида: А, В и С. Их предпочтения могут складываться так, как изображено на рис. 4.4, но могут и так, как показано на рис. 4.5.

На обоих рисунках АВ, ВС и АС – контрактные линии. На рис. 4.5 АВ и ВС лежат на АС. В такой специфической ситуации, несмотря на двумерный (в общем случае – многомерный) характер альтернатив, они как бы выстраиваются на одной шкале, и участник выбора В оказывается медианным избирателем. Вместе с участником А он способен забаллотировать выбор С, а вместе с С – выбор А. В конечном итоге точка В обеспечивает компромисс между A и С и является устойчивым результатом коллективного выбора.

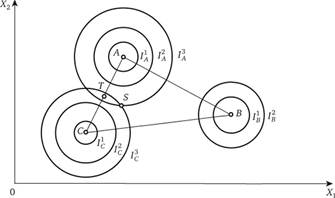
Рис. 4.4. Невозможность устойчивого результата выбора для трех индивидов

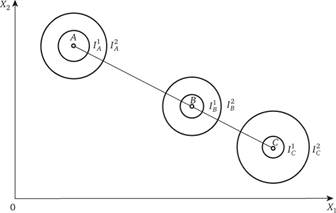
Рис. 4.5. Возможность устойчивого результата выбора для трех индивидов

В ситуации же, представленной на рис. 4.4, устойчивый результат недостижим. Представим себе, что выбран вариант, соответствующий точке S. Этот вариант Парето-эффективен, как и любой другой, отвечающий точкам, которые расположены на границах и внутри треугольника АВС. Но при наличии трех участников двое из них могут вступить в коалицию, дабы улучшить свое положение за счет третьего. Это произойдет, например, если индивиды А и С договорятся избрать решение Г вместо S. Легко видеть, что Т по сравнению с S ближе как к А, так и к С. В то же время Т дальше, чем S, по отношению к точке В. Ясно, что аналог медианного избирателя может быть найден не только при совпадении контрактных линий, как на рис. 4.5, но и вообще, если предпочтения всех участников голосования, кроме одного, уравновешивают друг друга.

Обратимся к рис. 4.6, на котором обозначены идеальные точки пяти голосующих индивидов. Какую бы прямую мы ни провели через точку Е, по обе стороны линии окажется равное количество идеальных точек других участников выбора. Получается, что при любом разделении плоскости, образуемой осями Х1 и Х2, если только разграничительная прямая проходит через точку Е, эта точка занимает в некотором смысле медианное положение по отношению к остальным. Голоса А и В уравновешиваются голосами С и D, голоса В и С – голосами А и D и т.д. В результате позиция избирателя Е оказывается решающей. Таким образом, представление о медианном избирателе может быть распространено на случай двумерных (и более общо – многомерных) альтернатив.

Доказано, что для таких альтернатив устойчивый результат коллективного выбора существует тогда и только тогда, когда один

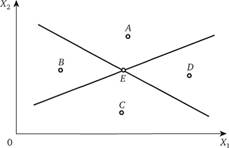
Рис. 4.6. Позиция медианного избирателя в случае двумерных альтернатив

из участников голосования занимает медианное положение в описанном выше смысле. Это значит, что по любую сторону всякой проходящей через медианную идеальную точку гиперплоскости размерностью на единицу меньшую, чем размерность альтернатив, оказывается не менее половины идеальных точек всех участников выбора.