Кинематический анализ механизмов

Кинематический анализ состоит в определении параметров движения звеньев механизма по заданному движению ведущих звеньев без учета действующих сил.

Основными задачами кинематического анализа являются:

• определение положений звеньев механизма и построение траекторий отдельных точек;

• определение скоростей точек и угловых скоростей звеньев;

• определение ускорений точек и угловых ускорений звеньев.

При решении задач кинематического анализа должны быть заданы:

• кинематическая схема механизма, а следовательно, структура механизма и размеры его звеньев;

• закон движения ведущего звена в виде зависимости перемещения звена (линейного или углового) или точки на нем от времени или других параметров движения.

В связи с этим кинематическому анализу должно предшествовать исследование структуры механизма, при котором определяется, сколько, какого класса и в какой последовательности соединены структурные группы, образующие ведомую кинематическую цепь механизма. Задачи кинематического анализа могут быть решены графическими или аналитическими методами. Выбор метода определяется назначением расчета и требуемой точностью решения.

Графические методы основаны на геометрическом построении траекторий движения отдельных точек звеньев механизма, их скоростей и ускорений. Получаемые результаты дают наглядную картину движения звеньев механизма и его точек. Однако для этих методов характерны трудоемкие построения и малая точность. Графическими методами нельзя получить общее решение, так как необходимые построения выполняются для каждого конкретного положения механизма.

Аналитические методы отличаются большим разнообразием математических подходов. Они основаны на использовании методов аналитической геометрии, тензорно-матричных операций, векторного анализа и др. Аналитические методы обеспечивают высокую точность вычисления искомых параметров для каждого момента времени работы механизма. Однако в ряде случаев из-за сложности математических преобразований утрачивается наглядность картины изменения исследуемых параметров. В настоящее время преимущественно применяют аналитические методы. Тем не менее для предварительной оценки кинематических параметров механизма и контроля аналитических вычислений используются простейшие геометрические построения – планы положений, скоростей и ускорений.

Кинематический анализ механизмов графическим методом

Решение задач о положениях, скоростях и ускорениях графическим методом поясним на примере кинематического анализа механизма плоского шарнирного четырехзвенника (рис. 1.12, а). Механизм имеет одну степень подвижности и состоит из ведущего звена 1 (кривошипа) и стойки О, к которым присоединена одна группа Ассура 2-го класса, составленная из звеньев 2 (шатуна) и 3 (коромысла). За обобщенную координату выберем угол поворота кривошипа φ1.

Задача о положениях (см. рис. 1.12, а). Решить задачу о положениях, т.е. построить план положений, – значит графически изобразить кинематическую схему механизма для

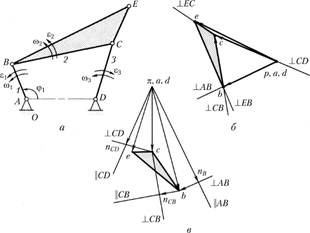
Рис. 1.12

заданного значения координаты 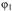. Для построения схемы механизма выберем масштабный коэффициент (м/мм):

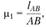
где 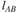– длина звена 1, м; АВ – отрезок, изображающий звено 1 на чертеже, мм.

Длины отрезков на чертеже, изображающих звенья механизма, представим в виде

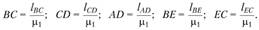
Вычислив длины отрезков, простым геометрическим построением получим план положения механизма для данного значения угла (φ1 (см. рис. 1.12, а).

Задача о скоростях (рис. 1.12, б). Данную задачу решают методом построения плана скоростей. Планом скоростей (ускорений) называется фигура, составленная из векторов абсолютных скоростей (ускорений) точек звеньев, выходящих из одной точки р ( для плана ускорений), называемой полюсом плана скоростей (ускорений), и векторов относительных скоростей (ускорений), соединяющих концы векторов абсолютных скоростей (ускорений).

Сначала для заданного положения механизма (задано значение угла 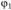) с известными размерами его звеньев строится план положений. При заданной угловой скорости ведущего звена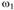требуется определить угловые скорости 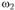, ω,-j звеньев 2, 3, а также скорости характерных точек В, С и Е звеньев механизма (см. рис. 1.12, а).

Скорость точки В ведущего звена vB (м/с) и масштабный коэффициент 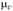(мс_1/мм) определяются выражениями

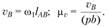
Здесь (pb) – длина отрезка, изображающего скорость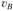 па плане скоростей (выбирается произвольно).

Для построения плана скоростей составляются два векторных уравнения скоростей на каждую группу Ассура 2-го класса, начиная с первой группы, присоединенной к ведущему звену. Скорости точек, принадлежащих внешним кинематическим парам группы, известны: 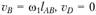Искомой является скорость точки С, принадлежащей внутренней кинематической паре группы, а следовательно, звеньям 2 и 3 одновременно.

Первое уравнение скоростей запишем, рассмотрев движение звена 2. Шатун 2 совершает плоскопараллельное движение, поэтому абсолютную скорость точки С можно представить суммой скоростей переносного и относительного движений. Переносным движением является поступательное движение звена 2 со скоростью точки В, а относительным – вращательное движение этого звена вокруг точки В. Используя теорему сложения скоростей, имеем

(1.5)

где 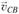– вектор скорости точки С во вращательном движе

нии звена 2 относительно точки В.

По аналогии составим второе векторное уравнение скоростей для движения звена 3:

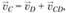(1.6)

где 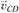– вектор скорости точки С во вращательном движении звена 3 относительно неподвижной точки D.

Приравняв правые части равенств (1.5) и (1.6), получим уравнение, которое непосредственно используется при построении плана скоростей:

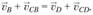(1.7)

Для плоской задачи векторное уравнение равносильно двум скалярным уравнениям, из которых можно определить две неизвестные величины 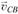и 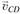. Их находят построением векторных треугольников скоростей – плана скоростей.

Построение плана скоростей начинаем с выбора полюса: на плоскости чертежа отмечаем произвольную точку р (см. рис. 1.12, б). Из полюса р откладываем отрезок (pb) произвольной длины, направленный перпендикулярно звену AB в сторону, соответствующую направлению вращения звена АВ. Затем из точки b проводим линию действия вектора 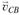, перпендикулярную звену СВ, и выполняем построение векторного треугольника, соответствующего правой части уравнения (1.7). Так как 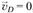, конец вектора 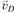(точка d на плане скоростей) совпадает с полюсом р. Из точки d проводим линию действия вектора 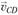, направленную перпендикулярно звену CD. Пересечение построенных линий (точка с) определяет положение конца вектора скорости 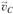. Вектор скорости изображается на плане скоростей отрезком (cb).

При определении направлений векторов на плане скоростей руководствуемся следующими правилами. Вектор абсалютной скорости всегда направлен из полюса; вектор относительной скорости – к точке плана, соответствующей первой букве индекса в обозначении этой скорости. Таким образом, стрелку вектора 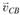на плане скоростей направляем из точки b в точку с. Вектор 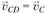, изображаемый отрезком ,также направлен в точку с плана.

Учитывая, что точка А звена АВ неподвижна, соответствующую точку а на плане совмещаем с полюсом р. На этом заканчивается построение плана скоростей механизма. Значения искомых скоросте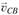йи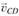находятся путем замера длин отрезков (cb) и (cd):

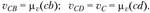
При определении угловых скоростей звеньев механизма используем полученные выше результаты. Модуль угловой скс роста вращения шатуна (звена 2) подсчитываем по формуле

Для определения направления вращения шатуна со скоростью ω2 перенесем вектор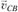параллельно самому себе из плана скоростей в точку С механизма. Направление вектора 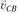показывает, что вращение шатуна будет направлено против хода часовой стрелки.

Аналогичные операции проводим при определении угловой скорости вращения звена 3:

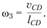
Параллельный перенос вектора vCd в точку С механизма позволяет установить, что вращение звена 3 с угловой скоростью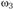направлено, как и вращение шатуна 2, против хода часовой стрелки. На схеме механизма, изображенной на рис. 1.12, а, направления вращения звеньев указаны круговыми стрелками.

После построения плана скоростей и определения угловых скоростей звеньев механизма появляется возможность определения скорости любой точки механизма. Допустим, требуется найти скорость точки Е шатуна 2 (см. рис. 1.12, а). Составляем два векторных уравнения, аналогичных уравнениям (1.5) и (1.6):

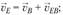(1.8)

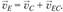(1.9)

Направление векторов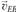 и: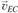

Объединим уравнения (1.8) и (1.9) в одно равенство:

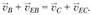
Теперь можно определить абсолютную скорость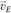, достроив план скоростей. Из точки b плана проводим линию, перпендикулярную BE, а из точки с – линию, перпендикулярную СЕ. Точка е пересечения этих линий определяет положение конца вектора 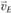. Соединив точку е с полюсом р, получим отрезок (ре), с помощью которого вычисляем значение скорости:

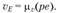
Обратим внимание на следующее свойство плана скоростей. Стороны 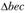плана скоростей и АВЕС плана положений механизма взаимно перпендикулярны, а следовательно, эти треугольники подобны. Вершины треугольников сходственно расположены, т.е. обход контуров (bес) и (ВЕС) происходит в одном направлении, в данном случае по ходу часовой стрелки. Это свойство справедливо как для плана скоростей, так и для плана ускорений любых точек одного и того же звена механизма. Оно формулируется в виде теоремы подобия: отрезки прямых, соединяющих концы векторов абсолютных скоростей (ши ускорений) точек одного и того же звена на плане скоростей (или ускорений), и отрезки прямых, соединяющих соответствующие точки самого звена на плане положений механизма, образуют подобные и сходственно расположенные фигуры [12].

С помощью этой теоремы можно найти скорость (или ускорение) любой точки звена путем построения подобных и сходственно расположенных фигур по известным скоростям двух точек этого звена.

Задача об ускорениях (рис. 1.12, в). Для определения ускорений точек звеньев механизма построим план ускорений. Построения проведем на примере того же шарнирного четырехзвенника при заданном значении обобщенной координаты φ1. Считаются известными угловая скорость ω1 и угловое ускорение ε1 ведущего звена.

Как известно, ускорение любой точки звена, совершающего вращательное движение вокруг неподвижной оси, можно представить суммой

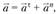
где 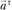и – соответственно касательная (тангенциальная) и нормальная составляющие ускорения .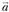

Ведущее звено (кривошип) четырехзвенника вращается вокруг точки А. Поэтому ускорение точки В

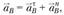(1.10)

где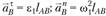

Нормальная составляющая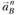ускорения точки В направлена к центру вращения (к точке A) параллельно АВ. Касательная составляющая 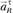направлена перпендикулярно АВ в сторону, совпадающую с направлением ускорения ε1.

На плане ускорений конец вектора нормальной составляющей ускорения точки обозначим буквой п с соответствующим точке индексом: пB – конец вектора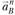на плане ускорений; пСВ – конец вектора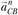

Зададимся отрезком 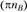, изображающим нормальную составляющую ускорения точки В, и определим масштабный коэффициент плана ускорений (в м-с-2/мм):

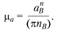
По аналогии с задачей о скоростях составим два векторных уравнения для ускорения точки С, принадлежащей звеньям 2 и 3:

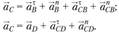
Отсюда

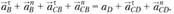(1.11)

В уравнении (1.11) aD = 0, а ускорения 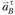и 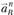уже определены по величине и направлению. Значения 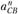и 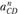вычисляем по формулам 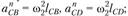отрезки, ко

торые изображают эти ускорения на плане ускорений (см. рис. 1.12, в), – по формулам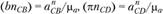

Построение плана ускорений проводим непосредственно по уравнению (1.11). От произвольной точки π откладываем отрезок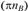параллельно AВ в направлении от В к A.

Из точки пв проводим отрезок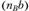, изображающий ускорение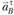. Соединив точку b с полюсом π, получим отрезок (πb), изображающий ускорение 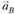. Стрелки, указывающие направление полученных векторов, расставляются согласно правилу векторного суммирования.

Для завершения построения левой части уравнения (1.11) из точки b откладываем отрезок 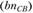параллельно шатуну 2 в направлении от точки С к точке В, а из точки пСВ перпендикулярно шатуну проводим линию действия вектора.

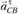При построении ускорений, расположенных в правой части (1.11), учтем, что 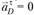, и совместим точку d плана ускорений с полюсом π. Из точки d построим параллельно CD отрезок 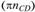, направленный от точки С к точке D и изображающий вектор 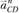. Из точки 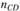перпендикулярно CD проведем линию действия вектора 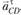, Пересечение линий действия ускорени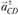й и 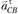определит точку с – конец вектора искомого ускорения 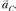. Соединяя точку с и полюс π, замерим длину отрезка 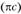. Закончив построение плана ускорений, находим неизвестные ускорения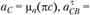 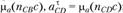; а затем – угловые ускорения звеньев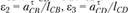

Направления ускорений ε2 и ε3, условно показанные на рис. 1.12, а круговыми стрелками, определяют векторы 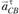и 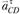, перенесенные с плана ускорений в точку С механизма.

Для нахождения ускорения аЕ точки Е шатуна используем свойство подобия плана ускорений. На отрезке (bс) плана ускорений строим 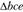, подобный 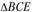плана положений и сходственно с ним расположенный. Полученную точку е соединим с полюсом π. Тогда .

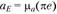Аналогичными построениями определяется ускорение любой другой точки механизма.