Дифференциальные уравнения равновесия жидкости

Выделим в жидкости, находящейся в равновесии, элементарный параллелепипед с ребрами dx, dy, dz, параллельными осям координат х, у, z (рис. 3.6). Выберем в центре параллелепипеда точку А. Давление в этой точке будет р = f(х, у, z). Так как это давление является непрерывной функцией координат, то, разлагая функцию f(х, у, z) в ряд Тэйлора в окрестности точки А с точностью до бесконечно малых первого порядка, получим следующие соотношения для давлений р1 и р2 в точках 1 и 2 на гранях параллелепипеда, перпендикулярных оси х:

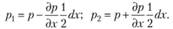
Давления на гранях параллелепипеда можно также записать в виде отношения силы к площади:

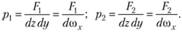(3.9)

Запишем условие равновесия сил, действующих на элементарный параллелепипед, в проекции на ось х:

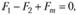(3.10)

где Fm – массовая сила, определяемая по формуле

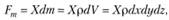(3.11)

где dm – масса элементарного параллелепипеда.

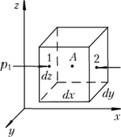
Рис. 3.6. Схема сил, действующих на элементарный параллелепипед

Подставляя формулы (3.9), (3.11) в соотношение (3.10), получаем

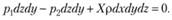
Подставляя формулы для р1 и р2, найдем

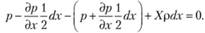
Отсюда

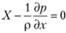
Аналогичные уравнения можно получить, если спроецировать действующие на параллелепипед силы на оси у и z. В итоге будем иметь систему трех дифференциальных уравнений вида

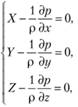(3.12)

где X, Y, Z – проекции ускорений массовых сил, приходящихся на единицу массы.

Эти уравнения впервые были выведены Эйлером в 1755 г. и называются уравнениями равновесия Эйлера. Они показывают, что при равновесии жидкости массовые силы уравновешиваются соответствующими поверхностными силами.

В векторной форме эти уравнения имеют вид

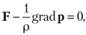
где 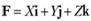; 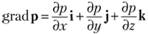(i, j, k – орты координатных осей, имеющие координаты (1; 0; 0), (0; 1; 0), (0; 0; 1) соответственно).

Потенциал массовых сил

Умножая уравнения Эйлера (3.12) соответственно на dx, dy, dz и почленно складывая, получаем

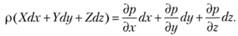(3.13)

Так как р = f (x, y, z), полный дифференциал этой функции будет

Следовательно, правая часть уравнения (3.13) есть полный дифференциал:

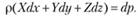(3.14)

Равенство (3.14) имеет смысл лишь в том случае, если левая его часть есть также полный дифференциал какой-то функции. Обозначим эту функцию через и = и(х, у, z). Тогда полный дифференциал ее будет

Примем, что

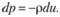(3.15)

Из сопоставления уравнений (3.14), (3.15) получим

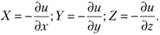
Функцию и = и(х, у, z) называют потенциальной функцией, а силы, для которых эта функция существует, – силами, имеющими потенциал.

Отсюда вывод: жидкость может находиться в равновесии только под действием массовых сил, имеющих потенциал, так как только такие силы удовлетворяют уравнениям равновесия Эйлера.

Интеграл уравнений Эйлера для несжимаемой жидкости

Проинтегрируем уравнение (3.15) при р = const:

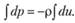
Отсюда

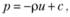(3.16)

где с – постоянная интегрирования. Полагая, что при р = р0 потенциальная функция и = u0, будем иметь

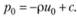
Отсюда

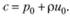(3.17)

Подставляя выражение (3.17) в соотношение (3.16), получаем

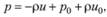
или

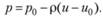
Последнее соотношение является интегралом уравнений Эйлера для несжимаемой капельной жидкости.

Так как величина ρ(u-u0) не зависит от давления р0 и определяется лишь системой массовых (но не поверхностных) сил, следовательно, на сколько изменится давление p0, на столько же изменится и давление р в любой точке жидкости. Отсюда можно сформулировать закон Паскаля: давление в жидкости, находящейся в равновесии, передается всем ее частицам без изменения сто величины.

Введем понятие поверхности равного давления и выведем ее уравнение.

Поверхностью равного давления называется такая выделенная в жидкости поверхность, гидростатическое давление во всех точках которой одно и то же. Для такой поверхности, очевидно, dp = 0. Так как р = f(x, у, z), уравнение поверхности равного давления р = const будет

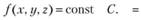
Придавая С различные значения, будем переходить от одной поверхности равного давления к другой. Это уравнение является уравнением семейства поверхностей равного давления. Поверхности равного давления и равного потенциала совпадают. Так как -ρdu = dp, при dp = 0 du = 0 и и = const.

Определение поверхности равного давления по заданным массовым силам производится по уравнению

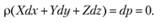(3.18)

Ввиду отсутствия массовых сил по осям х, у и с учетом того, что массовая сила по оси z Z = -g, уравнение (3.18) примет вид -ρgdz = 0, или dz = 0. Отсюда z = const.

Следовательно, поверхности равного давления, в том числе и свободная поверхность, – горизонтальные плоскости.