Понятие тензора скорости деформации

Пусть частицы среды движутся со скоростью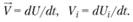

В течение бесконечно малого промежутка времени среда испытывает бесконечно малую деформацию, определяемую вектором перемещения Ui = Vidt.

Тогда аналогично тензору деформации сдвигов тензор скоростей деформации можно представить в виде

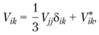(4.7)

где 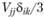– шаровой тензор, характеризующий скорость растяжения (сжатия); 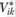– девиатор скорости деформации.

Кроме скорости деформации, характеризующейся тензором, элементарный объем среды испытывает жесткое смещение с поступательной скоростью 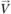и вращение с угловой скоростью

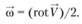(4.8)

Ускорение движущейся частицы среды определяется полной производной скорости:

(4.9)

Первый член этого уравнения характеризует локальные изменения скорости, второй – изменение вследствие переноса частицы в соседнюю точку пространства.

В каждой точке сплошной среды напряженное состояние характеризуется симметричным тензором напряжений δik.

В расписанном по компонентам виде он представляет собой матрицу

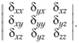(4.10)

Тензор 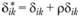называется девиатором напряжений (где r – плотность среды), а интенсивность касательных напряжений равна

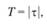(4.11)

где τ – главное касательное напряжение.

Уравнение движения и закон Гука

Уравнение движения имеет вид

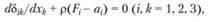(4.12)

где Fi – компоненты вектора массовой силы.

Если тело, подвергнутое деформации под воздействием внешних нагрузок, после снятия их возвращается к исходному виду, то деформации такого вида называются упругими. Уравнение состояния упругого тела являет закон Гука:

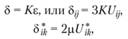(4.13)

где δ – тензор напряжения; К – модуль объемного сжатия; μ – модуль сдвига.

Первое выражение описывает связь между относительным изменением объема и всесторонним сжатием. Второе – связь между деформациями сдвига и касательными напряжениями.

Модули объемного сжатия и сдвига определяются выражением

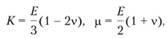(4.14)

где Е – модуль Юнга; ν – коэффициент Пуассона.

Модуль Юнга описывает уравнение движения

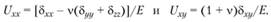(4.15)

В инвариантном виде закон Гука можно записать

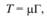(4.16)

или через девиатор напряжений

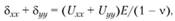(4.17)

или через оператор Лапласа

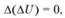(4.18)

где AU – функция напряжения, которая является бигармонической.

Таким образом, изучение плоской задачи теории упругости сводятся к исследованию бигармонического уравнения, поясняющго действие взрыва в упруго-хрупких материалах, образование осколков и трещин.

Математическая теория пластичности и уравнение Леви – Мезиса

Если деформированное тело после снятия внешней нагрузки не возвращается в исходное состояние, а имеет остаточные деформации, то говорят, что имела место пластическая деформация.

Условие пластичности можно выразить математически, с помощью компонент напряжения

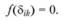(4.19)

Для описания пластической деформации грунтов и разрушенных горных пород наиболее часто используют уравнение Леви-Мезиса, наиболее точно описывающее этот процесс.

Для главных значений девиатора напряжений 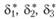и тензора скоростей пластической деформации 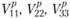можно получить выражение

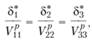(4.20)

отсюда для главных касательных напряжений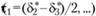 и главных скоростей деформации сдвига 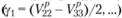получаем:

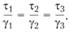(4.21)

Эти соотношения называется уравнением Леви-Мезиса. Они имеют ту же форму, как и уравнения, описывающие течение несжимаемой вязкой жидкости.

Только в случае жидкости коэффициент пропорциональности есть константа вещества (коэффициент вязкости), а для пластичных твердых тел это коэффициент равен l/λ*, где λ* является функцией напряжения и деформации.

Применительно к действию взрыва в грунтах и горных породах имеем:

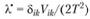(4.22)

(условие пластичности Мезиса).