Лекция 5. ТЕОРИЯ И ПРАКТИКА ПРИМЕНЕНИЯ МЕТОДОВ ОПТИМИЗАЦИИ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ
В результате изучения данной главы студент должен:
знать
• методы и механизмы принятия решений при исследовании конкретных социально-экономических объектов и управлении ими;
• различие и особенности нестационариости, неопределенности, неоднородности социально-экономических объектов;
• различие детерминированных, вероятностных и нечетких систем;
• возможности применения формализмов теории распознавания образов, игровых, логико-лингвистических, нейронных моделей;
• методы построения признакового пространства исследования сложных социально-экономических систем;
• особенности однокритериальной и многокритериальной постановки задачи оптимизации;
• сущность вариационных методов оптимизации, линейного, нелинейного, динамического, целочисленного программирования;
• методы анализа игровых ситуаций в экономике и менеджменте;
уметь
• формировать критерии и ограничения задачи принятия решений;
• формировать модель исследуемого процесса (экономического, социального, технологического и т.д.) и модель принятия решения;
• оценивать нестационарность и неопределенность, а также выявлять неоднородность coциально-экономических объектов;
• формулировать на языке математики оптимизационные задачи экономики и менеджмента;
• оценивать многокритериальную задачу на основе принципов Парето;
• решать с помощью стандартных пакетов программ задачи линейного, нелинейного программирования;
• формулировать постановку игры с прямоугольной платежной матрицей и нулевой суммой выигрыша;
владеть
• методами формализации задачи принятия решения (постановкой ее на языке математики);
• методами и технологиями идентификации критериев и ограничений оптимизации конкретных экономических и управленческих задач;
• программным обеспечением моделирования экономических процессов и их оптимизации;
• алгоритмом максимальной алгоритмической надежности принимаемого управленческого решения;
• технологиями построения платежных матриц.
Формализованная постановка принятия и реализации управленческих решений
Принятие решений в экономике, производстве и бизнесе базируется на знании основ экономической теории, кибернетических подходов к управлению, методов математического моделирования сложных социально-экономических объектов и процессов, а также процедур принятия решений.
Изложение и изучение данного вопроса имеет значимую учебно-методологическую ценность, здесь хорошо прослеживаются и укрепляются межпредметные связи различных дисциплин, изучаемых в высшей школе:
• общепрофессиональных математических дисциплин (функциональный анализ и линейная алгебра, теория вероятностей и математическая статистика, теория оптимального управления и теория игр);
• дисциплин и различных тем менеджмента (стратегический, тактический, оперативный, производственный и финансовый менеджмент, функции менеджера по А. Файолю, функции принятия решений по Г. Минцбергу, теория изменений и др.);
• различных курсов экономической теории (макро- и микроэкономика, экономики отраслей и регионов и др.);
• дисциплин прикладной информатики, а также дисциплин "по выбору" – теория массового обслуживания, теория нечетких множеств, теневая экономика и др.
Таким образом, важнейшей методологической ролью излагаемого ниже материала является систематизация разрозненных знаний ранее изучаемых различных дисциплин, обозначение их практической полезности, повторение и закрепление полученных ранее знаний через призму решения проблем принятия решений в менеджменте и экономике.
Цель раздела – ознакомление с методами и механизмами принятия решений при исследовании конкретных социально-экономических систем (СЭС) и управлении ими.
Принятию сложных решений в СЭС предшествуют этапы постановки цели, формирования критериев и ограничений задачи, выявления условий функционирования исследуемого объекта (системы), обоснования возможных вариантов решений. В элементарных случаях, когда нет альтернатив, путь к выполнению цели однозначен. В более сложных случаях указание известных исходных данных и цели, которые преследует разработчик, не определяет единой последовательности действий (пути). Для достижения цели необходимо провести:
• формализацию задачи принятия решения (постановку ее на языке математики);
• расчет оптимального пути к цели (вычислительная часть процесса принятия решения).
Обе задачи обладают лишь относительной самостоятельностью. Выбор средств и методов математических расчетов зависит от уровня достоверности и объема исходных данных, от априорной информированности ЛПР об исследуемом процессе. Правильная постановка задачи решающим образом влияет на корректность применения избранного математического аппарата.
Выше, в гл. 1–4 уже рассмотрены частные схемы, описывающие различные постановки и механизмы принятия решений. Их общее упрощенное представление, актуальное для раскрытия сути формализованной постановки задачи принятия и исполнения решения, можно представить схемой, изображенной на рис. 5.1.
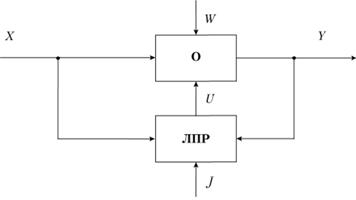
Рис. 5.1. Схема системы принятия решений:
О – объект исследования (бизнес-процесс, организация, коллектив сотрудников, производство, отраслевая или региональная экономика и т.д.), объект исследования характеризуется структурой взаимосвязи элементов f; ЛПР – лицо, принимающее решение (человек – менеджер, специалист; группа людей – эксперты, менеджмент компании; машина – в автоматических системах принятия решений); X – вектор входных наблюдаемых параметров (спрос и предложение, цены на рынке, стоимости ценных бумаг и валют и т.д.); Y – результирующий вектор (прибыль компании, себестоимость и качество продукции, рентабельность производства), характеризующий деятельность всей рассматриваемой системы; W – вектор неизмеряемых возмущений на объект исследования (задержки при транспортировке сырья и продуктов, технические и технологические проблемы на производстве и т.д.), но требующих от процесса принятия решений учета и нечувствительности к этим возмущениям; U – вектор управляющих воздействий (решения ЛПР об объемах инвестиций, выборе продуктовой линейки, организации процесса управления и пр.); J – вектор критериев, диктуемый ЛПР внешним окружением системы (максимум прибыли компании, минимум себестоимости продукции, захват сегмента рынка, повышение конкурентоспособности)
Следует отметить, что одни и те же показатели деятельности могут одновременно представляться в различных векторах описываемой схемы. Так, например, себестоимость и рентабельность могут входить и в J, и в Y, а изменение спроса на продукт или благосостояния населения переходить из W в X при расширении функций измерительной системы и т.д.
Приведенная схема обосновывает порядок движения и преобразования информации. Действительно, основой принятия решений являются данные, которые поступают к ЛПР по различным каналам (прямым измерением исследуемых параметров СЭС, вычислительным расчетом, от экспертов и т.д.), искажаясь и "зашумляясь" (приобретая ошибку). Обработка такой информации требует развития вспомогательных (по отношению к процессу принятия решений) вычислительных процедур, которые рассмотрены в гл. 6 и 7.
Объект исследования характеризуется структурой f, которая может быть известна с различной степенью точности. Например, при исследовании временны́х рядов, характеризующих динамику экономических процессов, можно использовать автокорреляционные модели, модели скользящего среднего, смешанные модели. Они отличаются друг от друга по своей структуре и определяют существенные особенности процессов (инерционность, влияние внешних факторов). Для СЭС, как правило, характерна высокая степень неопределенности структуры.
В данном случае различаются: собственно модель исследуемого процесса (экономического, социального, технологического и т.д.) и модель принятия решения. Сходства и различия, особенности построения моделей рассмотрим на конкретных задачах. Модели, как и объекты, имеют разные структуры, которые подробнее исследованы в параграфе 5.2.
Задача 5.1. Рекламная деятельность предприятия. Задача управления рекламной деятельностью состоит в следующем. Необходимо найти оптимальную политику руководства предприятия (порядок и размер выделяемых средств на организацию и проведение рекламной кампании) в области рекламной деятельности, которая стимулирует объем продаж S(t) данного продукта (товара или услуги) в некоторый момент времени t. Условия для построения формальной (математической) модели могут быть различными. Вот один из логичных вариантов рассуждений: скорость изменения объемов продаж dS(t)/dt уменьшается пропорционально осуществленному объему продаж (такая постановка верна, если иных поставщиков продукции на рынке нет) и увеличивается пропорционально уровню рекламной деятельности u(t) в той части рынка, которая еще этим продуктом нс насыщена. Если принять эти условия, то математическая формулировка задачи будет следующей:
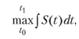 (5.1)
(5.1)
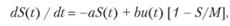 (5.2)
(5.2)
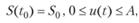 (5.3)
(5.3)
где М – емкость рынка; t0, t1, а, b, А – заданные положительные параметры.
Необходимо определить функцию u(t), обеспечивающую максимальное значение интеграла, аналитически определяющего интерес рекламодателя.
Соотношение (5.1) – критерий задачи оптимизации, сформулированный в форме Лагранжа, характеризует цель рекламной деятельности: достичь за заданный промежуток времени [t0, t1] максимального суммарного объема продаж.
Формула (5.2), имеющая вид дифференциального уравнения первого порядка относительно исследуемой величины S(t), и (5.3), представляют собой модель исследуемого процесса (структура f), связывающую входные (X = (М, t0, t, a, b, A, S )) и выходные (Y = S) данные, управление и(t) с результатом S(t).
Соотношение (5.3) определяет также ограничения задачи. В частности, в данной задаче принято, что в начальный момент времени t0 объемы продаж продукта равны S0, а диапазон изменения управления соответствует промежутку времени [t0, t1].
Численные значения обозначенных параметров задачи определяются в каждом конкретном случае на основании использования различных процедур.
1. Для вновь открывающегося бизнеса S0 = 0. В ином случае эта величина легко определяется из текущих отчетов деятельности фирмы. Величина 50 может быть задана экспертом или получена прогнозным расчетом, если задача оптимизации ставится для будущих периодов времени функционирования предприятия.
2. В качестве интервала планирования [t0, t1] целесообразно выбирать сроки финансовой отчетности предприятия, например квартал, год. Тогда t0 = 0, a t1 = 1. Если осуществляется перспективное планирование, то можно принять t0 = 1, а t1 = 2 и т.д.
3. Емкость рынка М ориентировочно оценивается по результатам мониторинга спроса и предложения данного продукта на рынке.
4. Показатель А отражает максимально возможные траты на рекламу данного продукта (оцениваются по финансовым возможностям фирмы) и на основании сравнения прироста ожидаемой прибыли от проведения рекламной кампании и затрат на ее проведение.
5. Коэффициенты а и b рассчитываются на основании результатов опытного использования рекламы из формулы (5.2) при заданных (измеренных) остальных переменных.
Процедура решения задачи (5.1)-(5.3) основывается на использовании принципа максимума Понтрягина. А именно: составляется функция Гамильтона – Понтрягина (как функция управления и(t)), определяется значение и(t), при котором она достигает своей верхней грани. Это и будет искомое решение.
Решение задачи 5.1 – пример строгой в математическом смысле постановки, которая используется в дисциплинах экономико-математического моделирования. Ее решение в одном частном случае для сравнения приведено в приложении 1.
Задача 5.2. Оптимизация выпуска продукции предприятия. Некоторая фирма выпускает однородную продукцию (товары или услуги). Из всей совокупности возможных различных воздействий среды на фирму известно одно: с – сложившаяся на рынке цена продукции, выпускаемой фирмой. Далее в числовом примере положим с = 6. Управляющим воздействием избрано и – количество выпускаемой фирмой продукции. Поставлена задача (сформулированы критерии): определить такой объем выпуска продукции, чтобы обеспечить максимум прибыли – J1 и (или) минимум себестоимости единицы продукции – J2. Для определения аналитических зависимостей прибыли и себестоимости (структура f) необходимо идентифицировать зависимость затрат у – выход объекта от количества выпущенной продукции.
Для решения последней поставленной задачи следует осуществить сбор информации о функционировании объекта. Примем, что в результате наблюдений получены результаты, представленные в табл. 5.1.
Таблица 5.1
Статистические данные зависимости затрат у от объемов производства и, усл. ед.
|
п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
и |
50 |
100 |
150 |
200 |
250 |
300 |
350 |
|
у |
200 |
400 |
650 |
900 |
1200 |
1600 |
2050 |
Используем простейший метод построения регрессионных моделей – метод наименьших квадратов. Данное программное обеспечение есть и в MS Exscel, и в достаточно распространенном программном продукте Statgraphics. Введя в программу данные, получим следующую зависимость затрат от объема выпускаемой продукции:
у = 0,01u2 + 2,07u + 85,7. (5.4)
Если в системе координат и0у построить график зависимости (5.4) и точки согласно данным табл. 5.1, то хорошо видно удовлетворительное соответствие эмпирических и теоретических данных (рис. 5.2).
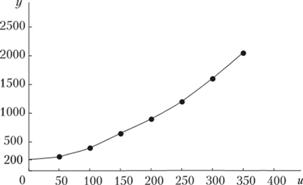
Рис. 5.2. Затраты на производство: эмпирические данные и теоретическая модель
На основании формулы (5.4) можно сформировать зависимости прибыли
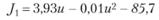 (5.5)
(5.5)
и себестоимости
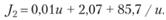 (5.6)
(5.6)
Выражение (5.5) является квадратичным с отрицательным старшим коэффициентом, потому J1 имеет только максимум, который принимается в точке х1 = 196,5 и равен max J1 = J1 (u1) = 300,4. Несложные вычисления позволяют найти так же точку u2 = 92,6, в которой себестоимость минимальна: min J2 = J2 (u2) = 3,93.
Точки и1 и и2 не совпадают по значению: и1 > и2, и это легко объяснимо, так как увеличение и (после значения и2) приводит к дополнительным затратам, из чего следует и увеличение J2 но эта продукция еще приносит прибыль. Если перед менеджером стоит одна из двух задач: или max J1 или min J2, то ее решение мы уже получили. Однако, как правило, фирма заинтересована в улучшении обоих показателей, т.е. возникает задача согласования противоречивых критериев. Классическая теория оптимальных решений предлагает целый спектр процедур для решения этой задачи (см. параграфы 5.3–5 .5).
Задача 5.3. Игра с природой. Сельхозпредприятие может высаживать на своих полях рис (Р) или пшеницу (П). Урожайность, а следовательно, и прибыль предприятия существенным образом зависят от степени влажности (сухости) года. При этом исследуемые сельскохозяйственные культуры по-разному реагируют на изменение общей влажности. Будем в дальнейшем различать только два класса погоды: влажный год – В и сухой год – С. Результаты функционирования предприятия при различных погодных условиях (влажная, сухая погода) и принятых решениях (высажены рис или пшеница) задаются табл. 5.2.
Таблица 5.2
Зависимость величины урожая от погодных условий (В или С) и принятых решений (Р или П), усл. ед.*
|
В |
С |
|
|
Р |
0,6 |
0,3 |
|
П |
0,3 |
0,7 |
* Если посажен рис и погода будет влажной, то выигрыш от этого решения составит в относительных единицах величину 0,6. Если же погода окажется засушливой, то эффект от посадки риса уменьшится вдвое и составит 0,3; если посажена пшеница во влажный год, то эффект равен 0,3, но при сухой погоде эффект возрастает до величины 0,7.
Данные для табл. 5.2 получаются статистическим путем на основе усреднения результатов наблюдений за значимый период времени. Понятие "значимый" предполагает, что период наблюдений достаточно большой, чтобы ошибки наблюдений по годам в средних характеристиках достаточно компенсировались, но и не столь протяженный, чтобы на результат могла повлиять нестационарность процесса.
Следующий необходимый для нас показатель – вероятность наступления влажного или сухого года. Он также рассчитывается статистически. Пусть наблюдения за влажностью последних 10 лет дали следующие результаты: В, С, С, С, В, В, С, В, С, С. Из этой последовательности, предполагая стационарность погодных изменений, можно заключить, что вероятность появления влажного года равна Р(В) = 0,4, а вероятность того, что год будет сухим, равна Р(С) = 0,6. Считается, что иных способов прогноза состояния погоды на данный момент нет. В противном случае появляется возможность уточнить искомые вероятности и повысить качество решения.
Средний выигрыш в этих условиях от посева риса составляет величину:
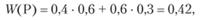
а средний выигрыш от посева пшеницы:
W(II) = 0,4 • 0,3 + 0,6 • 0,7 = 0,54.
Легко сделать вывод, что при прочих равных условиях (выполнение требований севооборота, заданий госзакупок и т.д.) выгоднее (в среднем) посадить пшеницу.
Задача 5.4. Классификация предприятий. С целью регламентации развития малого бизнеса в регионе группе экспертов поставлена задача: разработать механизм классификации предприятий малого бизнеса. Анализируя деятельность предприятий малого бизнеса в регионе по различным параметрам (число работающих, уставный капитал, оборот финансовых средств, инвестиции в основное производство, инновационность и т.д.), эксперты выделили совокупность предприятий, гарантированно отнесенных к успешным, и совокупность очевидно неэффективных предприятий. Эти совокупности положены в основу разрабатываемой классификационной схемы. Указанные признаки сравнения формируют так называемое признаковое пространство исследования, в котором каждый исследуемый объект представлен точкой. В табл. 5.3 представлен фрагмент массива данных, учитывающий только два признака из перечня указанных выше.
Таблица 5.3
Выборка данных, отн. ед.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
х1 |
0 |
0,3 |
1 |
0,9 |
0,6 |
0,2 |
0,7 |
0,6 |
0,3 |
1 |
0,7 |
|
х2 |
0,2 |
0 |
0,5 |
0,8 |
0,8 |
0,3 |
0,6 |
0,5 |
0,3 |
1 |
0,3 |
|
К |
Н |
Н |
Э |
Э |
Э |
Н |
Э |
Э |
Н |
Э |
? |
Примечание. Н – неэффективные предприятия; Э – эффективные предприятия.
В первой строке таблицы перечислены исследуемые предприятия, каждому из которых присвоен порядковый номер, во второй и третьей строках указаны соответствующие значения признаков х1 и х2, а в четвертой строке высказывается мнение экспертов о принадлежности исследуемого объекта к классу.
На рис. 5.3 изображено соответствующее двухмерное пространство признаков. Так как предприятия для списка табл. 5.3 задавались с ясно выраженной принадлежностью к выделенным классам, то на рисунке эти классы хорошо разделимы.
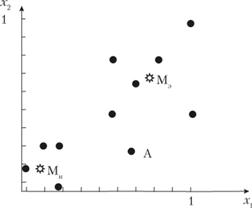
Рис. 5.3. Двумерное пространство признаков эффективных и неэффективных предприятий
Данные представлены в относительных единицах. Они переведены от исходных значений 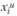 к безразмерному виду с помощью соотношений:
к безразмерному виду с помощью соотношений:
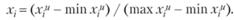
Эта процедура всегда переводит произвольный промежуток изменения 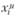 в интервал [0,1].
в интервал [0,1].
В первых 10 случаях принадлежность точек (предприятий) к классам известна. Это точки обучающей последовательности (см. рис. 5.3). В 11-м случае известны только координаты точки (параметры предприятия), и требуется определить ее принадлежность к одному из выделенных классов (на рисунке обозначена как точка Л).
Из множества возможных подходов для формирования решающего правила рассмотрим наиболее простой метод, а именно – метод эталонов. Сущность его состоит в следующем.
Для точек одного класса по всем признакам находятся средние значения. Они и определяют координаты вектора соответствующего эталона:
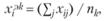 (5.7)
(5.7)
где k – номер эталона; пk – число точек k-m класса в обучающей выборке; j – номер предприятия соответствующего класса. Эталоны Мэ и Мн, рассчитанные с помощью формулы (5.7) по данным табл. 5.3, имеют координаты: Мэ (0,8; 0,7), Ми (0,2; 0,2), они представлены на рисунке звездочками.
В данной задаче рассматривается только два класса объектов, но их может быть несколько. Например: класс эффективных, класс устойчиво функционирующих, класс неэффективных предприятий. Если говорить о продуктах, то они могут быть разного качества: высшего, первого сорта, второго, некондиция (брак) и г.д. Аналогично работник может быть высококвалифицированным, квалифицированным, иметь среднюю или низкую квалификацию и т.д.
Теперь для любого заданного предприятия А с неизвестной классификацией достаточно найти "расстояния" до эталонов классов и по наименьшему из них определить принадлежность исследуемого предприятия к выделенным типам. Одновременно становится понятным механизм совершенствования деятельности предприятия. Оно осуществляется в направлении АМЭ. Чтобы предприятию А стать "эталонно эффективным", следует параметр 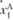 изменить на величину
изменить на величину 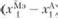 , а параметр
, а параметр 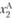 – на величину
– на величину 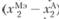 .
.
В последнем столбце табл. 5.3 даны координаты точки с неизвестной классификацией: А (0,7; 0,3). Определим расстояние от этой точки до эталонов. Для этого используем обычное евклидово расстояние, определенное формулой (5.8):
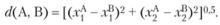 (5.8)
(5.8)
Итак: d(А, Мэ) = 0,260,5, d( А, Мb) = 0,170,5. Откуда следует, что предприятие с параметрами (0,7; 0,3) относится к классу эффективных.
В данном иллюстративном примере мы не обосновывали возможности применения евклидова расстояния в виде формулы (5.8), считая признаки предприятий, приведенные к безразмерному виду, равнозначными. Исследование случая, когда это условие нарушается, приведено в параграфе 6.2.
Данные, которыми приходится оперировать, исследуя социально-экономические объекты и процессы, характеризуются нестационарностью, зашумленностью, что часто приводит к ряду вычислительных проблем:
• отсутствие решения там, где оно на самом деле существует;
• неустойчивость вычислительных процедур (малым отклонениям в данных соответствуют значительные расхождения в решениях);
• возникновение множества решений-претендентов, требующих селекции по дополнительным критериям.
Такие математические задачи называются некорректно поставленными и требуют специальных регуляризированных методов решения. В качестве примера можно привести хорошо известный метод наименьших квадратов, используемый при идентификации неизвестных моделей по статистическим данным. Подробнее этот вопрос исследован в параграфе 6.1.
Задача 5.5. Идентификация моделей. Вернемся к процедуре построения модели (5.4), подобной приведенной в задаче 5.2. Она имеет вид
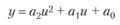 (5.9)
(5.9)
и содержит три неизвестных параметра аг
Если данные табл. 5.1 известны без ошибки, то достаточно из таблицы взять три независимых наблюдения, подставить соответствующие значения и и y в формулу (5.9), получить систему трех уравнений с тремя неизвестными и решить ее. Но данные в табл. 5.1 заданы с ошибками, поэтому система полученных уравнений не будет отражать реального соответствия между и и у, а система уравнений при их числе больше числа неизвестных (у нас больше трех) будет несовместной. В этом легко убедиться, исследовав систему уравнений, полученную по табл. 5.1 и с помощью формулы (5.9). Вот данная система уравнений:
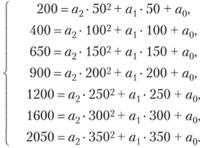 (5.10)
(5.10)
Регуляризованное решение данной системы находится следующим образом. Формируется регуляризирующий оператор – критерий, который необходимо минимизировать. В методе наименьших квадратов таковым критерием является сумма квадратов отклонений левых и правых частей системы уравнений вида (5.10). В нашем случае такой критерий задается соотношением:
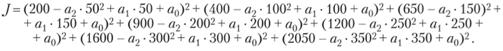
Далее решается обычная задача на нахождение экстремума: находятся частные производные функции J по искомым неизвестным коэффициентам а2, а1, а0, которые приравниваются к нулю, и решение вновь полученной системы принимается за искомые коэффициенты формулы (5.9). Такое решение системы (5.10) называется обобщенным решением.
Итак, рассмотренные примеры проиллюстрировали разные виды моделей исследуемого объекта: дифференциальное уравнение (задача 5.1), матрица, линейная функция многих переменных с ограничениями (задача 5.2), нелинейные функции (задача 5.3).