Теоретико-множественные представления и их применение при моделировании систем

Теоретико-множественные представления базируются па понятиях "множество", "элементы множества", "отношения на множествах".

Понятие множество относится к числу интуитивно постигаемых понятий, которым трудно дать определение. Оно содержательно эквивалентно понятиям "совокупность", "собрание", "ансамбль", "коллекция", "семейство", "класс" и другим обобщающим понятиям.

Один из основоположников теории множеств Г. Кантор определял множество как "многое, мыслимое нами как единое".

Множества могут задаваться следующими способами:

1) списком, перечислением (интенсиональным путем); например,

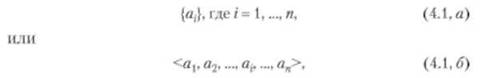
где а( е А , е — знак вхождения элементов в множество;

2) путем указания некоторою характеристического свойства А (экстенсионально). Например, "множество натуральных чисел", "множество рабочих данного завода", "множество планет солнечной системы", "множество А" и т.д.

В основе теоретико-множественных преобразований лежит принцип перехода от одного способа задания множества к другому:

Переход от интенсионального способа задания множества к экстенсиональному называют принципом свертывания.

В множестве могут быть выделены подмножества. Вхождение элементов в любое множество или подмножество описывается знаком "принадлежит" — є, а вхождение подмножества в множество записывается В с А.

Это означает, что все элементы подмножества В являются одновременно элементами множества Л (рис. 4.1).

Важным понятием является понятие пустого множества — множества, в котором в данный момент нет ни одного элемента: Б = 0.

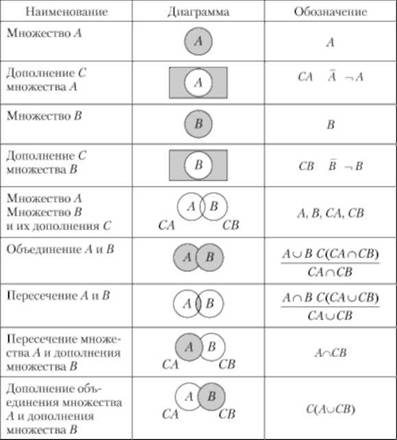
При использовании теоретико-множественных представлений в соответствии с концепцией Кантора можно вводить любые отношения. При уточнении этих отношений применительно к множествам удобно пользоваться наглядными диаграммами Эйлера — Венна, примеры которых для операции объединения (и), пересечения (& или о), дополнения (отрицания, обозначаемого знаком "-" над именем множества либо знаком перед именем множества или его элемента) приведены в табл. 4.1.

Теории, развивавшиеся на базе теоретико-множественных представлений, первоначально использовали отношения, подобные функциям алгебры логики, и в первую очередь — бинарной алгебры логики Буля (основные функции которой приводятся далее, в табл. 4.2).

В большинстве работ теоретико-множественные представления излагаются на примере теории чисел, для развития которой достаточно основных элементарных отношений е, ё,с, <2, с=, и, п, -..

По мере приложения теоретико-множественных представлений к более сложным проблемам отношения начинают заимствоваться из математической лингвистики (которую теория множеств, в свою очередь, помогает развивать), а при отображении особо сложных проблемных ситуаций с неопределенностью формируемую или исследуемую систему отображают множествами с отношениями произвольного типа (так, например, при применении теоретико-множественных представлений в ситуационном моделировании используются отношения "быть над", "быть под", "находиться рядом" и т.п., которые допустимо обозначать в разрабатываемом на этой основе языке моделирования произвольными символами, удобными для ЛПР).

Таблица 4.1. Основные функции бинарной алгебры логики Буля

Особого внимания заслуживает преобразование множеств путем установления взаимоотношений между элементами разных исходных множеств. Из двух или нескольких множеств можно сформировать путем установления отношений между элементами этих множеств новое множество. Его, как правило, следует рассматривать как множество, состоящее из принципиально новых элементов.

Например, объединяя элементы из множества "конденсаторы С" и множества "катушки индуктивности I", получим новое множество "колебательные контуры КК" (если, конечно, введенное отношение между исходными элементами отображает необходимые действия по объединению соответствующих выводов конденсаторов и катушек индуктивности). Аналогично можно отобразить процесс бракосочетания: из множеств "женихи У" и "невесты О" в загсе путем соответствующей операции (процедуры регистрации брака) формируется множество "семьи С", элементы которого сх = < у-, гк gJ >, где у е У, gj € (7, гк е /?„, /?„, — множество взаимоотношении между людьми, имеющих принципиально новый смысл для общества, и, кроме того, элементы этого множества изменяют свои названия — "муж" и "жена".

При этом важно отметить, что не только установление какого-либо вида специальных отношений, как в этих приведенных примерах, но и формирование элементов нового множества путем простого "помещения рядом" элементов исходных множеств позволяет получать эффект появления нового смысла, что обеспечивается доосмыслением взаимоотношений человеком на основе его предшествующего опыта. Это важно при моделировании ситуаций с большой исходной неопределенностью, когда неизвестен характер взаимоотношений между элементами разных групп (подмножеств), выявленных для отображения системы, проблемной ситуации.

Этот эффект используется при моделировании процесса структуризации целей, морфологическом моделировании. При использовании таких преобразований необходимо предварительно оценивать перебор. При получении нового множества из элементов двух, трех или более исходных подмножеств с математической точки зрения имеет место операция размещения с повторениями, при использовании которой число получаемых компонентов

где к{, —" К} ~ количества элементов в Мх, М, —, Мп подмножествах, что дает существенно меньший перебор, чем формирование сочетаний.

Между теоретико-множественными описаниями разных систем или их частей можно устанавливать соответствия. Для характеристики сходства множеств (подмножеств) можно использовать понятия гомоморфизма, изоморфизма, автоморфизма, отношения рефлексивности, симметричности, транзитивности*, заимствованные теорией множеств из других разделов математики.

"Изоморфизм" и "гомоморфизм" — логико-математические понятия, выражающие одинаковость (изоморфизм: от греч. /505 — одинаковый и morphe — форма) либо подобие (гомоморфизм: от греч. homoios — подобный) строения (структуры) систем, множеств, процессов, конструкций. Системы Л и Л, называются изоморфными (или находящимися в отношении изоморфизма), если между их элементами, а также функциями (операциями), свойствами и отношениями, осмысленными для этих систем, существует или может быть установлено взаимооднозначное соответствие. В этом случае каждая из систем Л и Л) называется изоморфным образом другой.

Для изоморфных систем выполняются следующие условия: 1) каждому элементу а из А соответствует единственный элемент Ъ из В (Ь е В), и наоборот; 2) каждой функции/, определенной на элементах Л и принимающей значения в Л, соответствует единственная функция g, определенная на элементах В, и наоборот; 3) каждому свойству Р, которым обладают какие-либо элементы системы Л, соответствует взаимооднозначное свойство элементов В, и наоборот.

Ослабление перечисленных условий — например, требование взаимооднозначного соответствия только в одну сторону — приводит к более общему, но и более слабому отношению гомоморфизма. Изоморфный образ полностью воспроизводит отображаемую систему, например, зеркальное отображение изоморфно отображаемому предмету, схема радиоприемника изоморфна самому приемнику. Гомоморфный образ лишь отчасти похож на свой оригинал, например, карта местности воспроизводит лишь некоторые черты этой местности, перевод языкового текста лишь отчасти похож на оригинал. Всякий изоморфизм есть гомоморфизм, но не наоборот.

При использовании надлежащих абстракций и идеализации под понятия изоморфизма и гомоморфизма могут быть подведены широкие классы отношений, существующие между системами различной природы (например, отношения между фотографией и оригиналом, переводом языкового текста на некоторый язык и подлинником, географической картой и соответствующей местностью, чертежом машины и самой машиной, разговорной речью и магнитной лентой, на которой она записана, движениями небесных тел и описывающей их системой дифференциальных уравнений и т.п.). Строго точно понятия изоморфизма и гомоморфизма реализуются в классической математике и математической логике.

Изоморфизм представляет собой отношение типа равенства. Отсюда проистекает его методологическое значение как средства обоснования правомерности переноса знаний, полученных при изучении одной изоморфной системы, на другую. В отличие от изоморфизма, гомоморфизм, не будучи симметричным отношением, обосновывает перенос знаний лишь с гомоморфного образа на прообраз, но не наоборот (любые знания, извлекаемые, например, из верной географической карты, переносимы на соответствующую местность, но не все, что имеется на местности, отображается на карте). Понятия изоморфизма и гомоморфизма используются для характеристики понятия модели и метода моделирования, а также гносеологической категории образа (если он фиксирован средствами какой-либо из знаковых систем).

Автоморфизм алгебраической системы — изоморфизм, отображающий алгебраическую систему па себя. Понятие автоморфизма введено в алгебре групп.

Совокупность всех автоморфизмов некоторой алгебраической системы с операцией композиции и тождественным отображением в качестве нейтрального элемента образует группу. Группа автоморфизмов алгебраической системы К обозначается Л и К

Наиболее простой пример автоморфизма — это автоморфизм множества, т.е. перестановка элементов этого множества. Понятие автоморфизма можно обобщить на более абстрактные объекты, не являющиеся "множествами с дополнительной структурой".

Для отображения систем важными понятиями являются понятия ординарного и экстраординарного множеств.

Если множество сформировано из геометрических фигур — например, треугольников — и принято условие, что формирование нового множества осуществляется в той же плоскости, то полученное новое множество будет также плоской геометрической фигурой, а возможно даже — и треугольником. Такие множества относят к классу ординарных. Аналогично можно посмотреть на множество колебательных контуров, которые так же, как конденсаторы и катушки индуктивности, являются элементами радиотехнических устройств. Однако, учитывая принципиально новые свойства колебательного контура, можно эту же ситуацию трактовать как формирование экстраординарного множества с принципиально новыми свойствами элементов. При формировании экстраординарного множества в примере с семьей изменяются не только свойства множества, но и суть и даже наименования исходных элементов ("жених" — "муж", "невеста" — "жена").

Важным понятием для освоения и использования теоретико-множественных представлений является понятие континуума (от латинского continuum — непрерывный) -связного обобщающего множества (т.е. как бы единого непрерывного пространства), в рамках которого осуществляются операции над множествами (их изъятие, добавление новых, объединение, пересечение и т.п.).

В простейших случаях континуум может быть задан границей, которая не изымается даже в случае, если исключаемое множество (подмножество) вплотную смыкается с этой границей (в примерах, приведенных в табл. 4.1, роль континуума играет прямоугольник). Роль континуума может играть пустое множество значительно больших потенциальных размеров, чем входящие в него подмножества. Но в более общем случае (особенно при отображении открытой системы, в которую могут постоянно включаться новые подмножества с непредсказуемыми границами) континуум формируется как внешняя граница всех пересекающихся или другим образом взаимодействующих подмножеств, с помощью которых отображается система.

Попятно, что в случае моделирования развивающихся систем континуум постоянно видоизменяется и его изменения, в том числе сохранение связности, нужно постоянно уточнять.

Благодаря тому что в соответствии с первоначальной концепцией Кантора при применении теории множеств допустимо введение любых произвольных отношений, теоретикемножественные представления стали использоваться как обобщающий язык при сопоставлении различных направлений математики и других дисциплин, явились основой для возникновения новых научных направлений или развития существующих.

В частности, первой теорией, для которой на основе теоретико-множественных представлений были получены новые результаты, была теория чисел. Теоретико-множественные представления сыграли большую роль в становлении комбинаторики, топологии, в разработке теории "размытых" множеств; на их основе стали создаваться первые информационно-поисковые языки, языки автоматизации моделирования. На теоретико-множественных представлениях базируется вариант математической теории систем М. Месаровича.

Использование теоретико-множественных представлений при моделировании систем позволяет организовать взаимодействие и взаимопонимание между специалистами различных областей знаний. С их помощью можно записать различные определения системы (что сделано в гл. 1) и выбрать из них то, которое в наибольшей степени отражает концепцию исследователей, проектировщиков.

Конкретная система при первоначальном описании может быть отображена теоретико-множественной формулой, включающей наборы различных элементов (например, Л, В, С); отношений между ними (й), которые могут быть также разделены на подмножества (#,, й, /?з и т.д.); свойств элементов 0^, О/,. 0<- и свойств отношений могут быть учтены множества входных воздействий X и выходных результатов У:

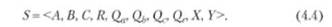
Затем, по мере накопления сведений о системе, теоретико-множественная формула (4.4) может измениться и отразить взаимоотношения между группами множеств:

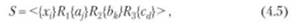
а в дальнейшем описание может уточняться: могут быть введены подмножества и отношения между ними и их элементами; деление на подмножества может быть повторено неоднократно, и таким образом с помощью теоретико-множественных представлений возможно отображение многоуровневой структуры; отношения могут быть уточнены в виде набора правил преобразования множеств или подмножеств.

Как было сказано ранее, при использовании теоретико-множественных представлений в принципе можно вводить любые отношения. Однако при произвольных отношениях в формализованном с их помощью описании проблемной ситуации довольно быстро могут обнаружиться неразрешимые противоречия — парадоксы, апории или антиномии, что не позволяет оперировать с получаемыми теоретико-множественными моделями таким же образом, как с классическими математическими соотношениями, и доверять достоверности получаемых результатов.

В качестве примеров парадоксов приводят обычно: парадокс лжеца (нельзя дать положительного ответа на вопрос "Ты лжешь?"): парадокс парикмахера, которому отдано распоряжение "брить всех мужчин в полку, которые не бреются сами".

Действительно, если попытаться формально записать ситуацию парадокса парикмахера, то возникает неразрешимое противоречие: парикмахер X принадлежит множеству одновременно мужчин М,, которые не бреются сами и которых но распоряжению он обязан брить, и множеству тех мужчин Л/2, которые бреются сами и которых согласно распоряжению он брить не должен, и эти множествам! и М не пересекаются и не входят друг в друга, т.е. должно иметь место: X е М], X е М. М = М, 11 М = 0. что невозможно.

Примеры парадоксов легко можно найти во многих высказываниях неформализованного текста: например, "Ты должен сам любить меня" (если "должен", то "нс сам"; если "сам" — то "не должен", а любит без принуждения).

На этом свойстве текстов основаны некоторые психологические тесты. Эта принципиальная особенность текстов не позволяет однозначно отразить с их помощью проблемные ситуации и требует перевода текстов в формализованные описания с использованием специализированных знаковых систем, языков, в которых по возможности устранены парадоксы. Для разработки таких языков могут быть использованы теоретико-множественные представления, которые позволяют выявлять и устранять парадоксы, ограничивая при этом свободу выбора отношений, т.е., строго говоря, огрубляя качественное описание, уменьшая его полноту. Однако такие ограничения при применении теоретико-множественных представлений можно делать осознанно, фиксировать и пересматривать при необходимости.