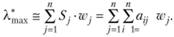Теорема

Матрица относительных весов 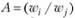имеет лишь два вещественных собственных значения: п и 0.

Если обозначить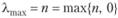, то в соответствии с теоремой равенство (2.5) можно представить в виде

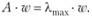(2.9)

Равенство (2.9) – основа для дальнейшей математической обработки и интерпретации экспертных оценок в рамках метода анализа иерархий.

На практике при проведении экспертного оценивания экспертам очень трудно одновременно сопоставить свойства всей группы сравниваемых объектов (факторов)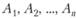, которых может быть весьма много, и назначить им соответствующие веса 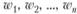. Куда легче сравнивать объекты попарно, характеризуя с помощью какой-либо шкалы оценок степень преимущества одного объекта над другим. Взвешивая экспертно превосходство одного объекта над другим и не удерживая в памяти все множество отношений между рассматриваемыми объектами, мы вправе рассчитывать на то, что экспертное оценивание будет более обоснованным и корректным. Схема попарного сравнения объектов широко используется в различных методах экспертного оценивания и приводит к построению матрицы парных сравнений

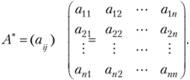(2.10)

Заполняя клетки этой матрицы, при парном сравнении эксперт не знает всего набора чисел 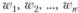, т.е. весов объектов. Его задача как раз и состоит в том, чтобы определить их впоследствии. При парном сравнении матрица заполняется числами 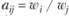, характеризующими относительное превосходство (важность, вес) объекта Ai над объектом Аj в то время как собственные веса этих объектов wi и wj пока еще не определены. Иными словами, aij назначается экспертом, а веса wi и wj, образующие при делении друг на друга величину аподлежат последующему определению.

Для назначения чисел необходимо договориться о шкале, по которой будет оцениваться превосходство одного объекта над другим при их попарном сравнении. Для целей экспертного оценивания примем 9-балльную шкалу, предложенную автором метода анализа иерархий Томасом Саати (табл. 2.1).

Таблица 2.1

Шкала относительной важности

Интенсивность относительной важности, балл	Определение	Объяснение
1	Равная важность	Важность объектов (факторов) Ai и Aj одинакова
3	Умеренное превосходство одного над другим	Опыт и суждения дают легкое превосходство одному объекту (фактору) над другим
5	Существенное или сильное превосходство	Имеющиеся данные свидетельствуют о заметном превосходстве Ai над Aj
7	Очень сильное превосходство	Превосходство объекта (фактора) Ai над Aj очевидно
9	Абсолютное превосходство	Очевидность превосходства Ai над Aj подтверждается всеми имеющимися признаками
2, 4, 6, 8	Промежуточные решения между двумя соседними суждениями	Применяются в компромиссных случаях

Шкала относительной важности содержит, очевидно, и все обратные числа 1/9, 1/7, 1/5, 1/3 и промежуточные значения 1/8, 1/6, 1/4, 1/2.

Матрица парных сравнений заполняется, как правило, следующим образом. Объект A1 сравнивают со всеми остальными A2, ..., An, заполняя последовательно первую строку матрицы. Затем объект A2 сравнивают со всеми остальными, заполняя вторую строку числами а-ф определяемыми по шкале относительной важности и т.д. Если вес объекта Ai равен весу объекта Aj, то сообразно шкале аij = 1. Если вес объекта Ai больше веса объекта Aj, то в соответствии со шкалой эксперт определяет степень превосходства, выраженную в баллах, причем 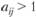. Если наоборот вес объекта А, меньше веса объекта Аj, то по шкале задается балльная оценка .

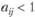По правилам заполнения матриц парных сравнений должны выполняться условия:

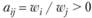для всех i и j, так как все балльные оценки положительны;

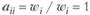для всех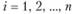

Элементы матрицы А обладают обратной симметрией, а именно 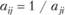, иначе говоря, если превосходство объекта А; над объектом Aj оценивается по шкале, например в 5 баллов и 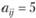, то обратное сопоставление объекта Aj с Ai должно автоматически давать оценку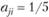

Очевидно, что в силу обратной симметричности при заполнении матрицы парных сравнений удобно найти только элементы, стоящие выше диагонали. Диагональные элементы равны единице, а элементы под диагональю в силу обратной симметричности определяются автоматически.

Необходимо обратить внимание на то, что матрица парных сравнений обладает всеми свойствами матрицы относительных весов в схеме идеального сравнения, кроме четвертого. Таким образом, она не обладает, вообще говоря, свойством совместности 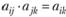. Это, очевидно, происходит из-за того, что эксперт не знает точно веса объектов 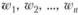, а оперирует лишь их отношениями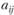

Можно найти максимальное вещественное собственное значение 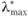и собственный вектор w* матрицы парных сравнений. Вообще говоря, 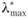и w* не совпадают с соответствующим собственным значением λmax = п и собственным вектором да матрицы относительных весов в схеме идеального сравнения. Можно доказать, что в общем случае имеет место неравенство 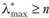, причем равенство достигается тогда и только тогда, когда матрица A' является совместной, т.е. выполняется четвертое свойство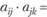

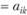
Идея Т. Саати состоит в том, что коэффициенты матрицы парных сравнений А* заданы сравнительно точно, т.е. отклонения аij от истинных отношений весов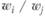незначительны. Тогда можно надеяться, что и 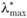будет близко к п. Здесь используется известное положение линейной алгебры, согласно которому малым отклонениям от исходных значений элементов матрицы соответствует малое отклонение ее собственных значений.

Определив одним из методов линейной алгебры, можно найти и вектор w* который будет мало отличаться от "истинного" вектора да. Вектор w* определяется, например из системы однородных уравнений

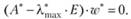(2.11)

Вектор w* удовлетворяющий условию нормирования

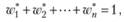(2.12)

как доказывается в линейной алгебре, всегда существует и определяется однозначно.

Применение предложенного подхода будет оправдано, если реальная ситуация окажется близкой к идеальной. В качестве меры отклонения реальной схемы от идеальной используется индекс совместности, определяемый по формуле

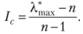(2.13)

Если IС < 0,2, то считается, что расхождение между идеальной и реальной схемами сравнения находится в допустимых пределах и полученным результатам можно доверять. Если это условие не выполняется, следует пересмотреть задачу, уточнить экспертные оценки и заново сформировать матрицу парных сравнений А

В частном случае п = 2 характеристическое уравнение любой обратно симметричной положительной матрицы с единичными диагональными членами будет иметь вид

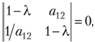
или, раскрывая детерминант,

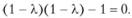
Последнее уравнение имеет два корня, которые равны 0 и 2. Таким образом, в этом частном случае всегда 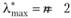, т.е. всегда имеет место полная согласованность (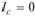), а значит, и полное совпадение реальной и идеальной схем сравнения.

Рассмотрим основные этапы определения весов объектов в соответствии с методом Т. Саати.

• Построить матрицу парных сравнений А* удовлетворяющую первым трем из перечисленных выше требований.

• Найти максимальное собственное значение 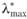для матрицы A* с помощью одного из известных математических численных методов. Приближенные методы определения собственных значений и векторов, не требующие использования ЭВМ, будут описаны в следующем разделе. Проверить, что .

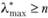• Определить собственный вектор w* исходя из уравнения (2.5) или, что удобнее, приближенным способом, который будет описан ниже.

• Выполнить нормирование вектора w*.

• Вычислить индекс согласованности по формуле (2.7). Убедиться, что 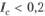. В том случае, если это условие не выполняется, необходимо переосмыслить задачу, задать другие экспертные оценки, заново составляя матрицу парных сравнений. Вектор w* является окончательным решением задачи.

Компоненты вектора w* приближенно определяют веса (значимость, интенсивность) сравниваемых объектов (факторов). Очевидно, что большие по величине компоненты соответствуют более важному (значимому) с точки зрения эксперта фактору.

В книге Т. Саати предлагаются следующие приближенные способы определения собственных значений и собственных векторов матрицы парных сравнений.

1. Алгоритм приближенного определения собственного вектора матрицы А*.

Если имеется матрица парных сравнений 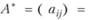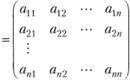, то компонента wi ее собственного вектора может быть приближенно вычислена по формуле

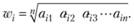(2.14)

2. Алгоритм приближенного вычисления собственного значения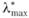матрицы А*:

а) найти сумму каждого столбца матрицы А*:

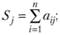
б) умножить сумму каждого столбца Sj на соответствующую по номеру компоненту wj нормализованного собственного вектора;

в) определить