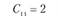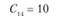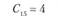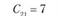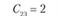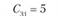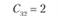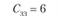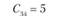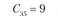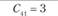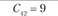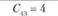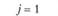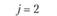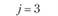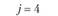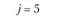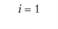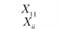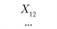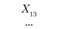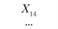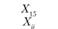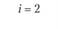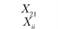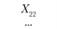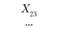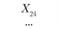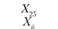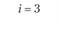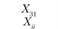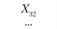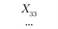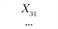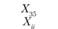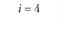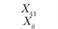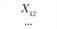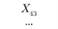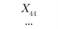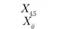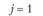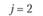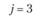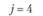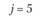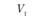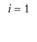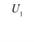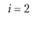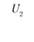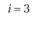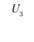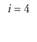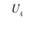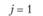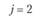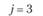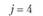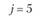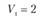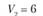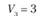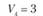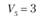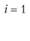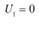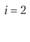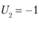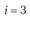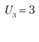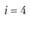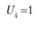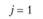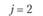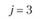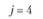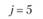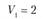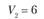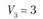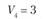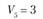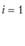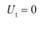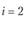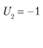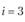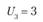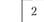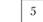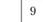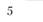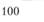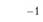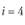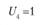Развозочный маршрут при перевозке мелкопартионных грузов потребителям
Постановка задачи. Заданы пункты потребления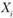 
(i = 1, 2, ..., п). Груз необходимо развезти из начального пункта 
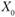(склад) во все остальные
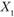(потребители). Потребность пунктов потребления в объеме поставки составляет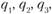
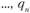. В начальном пункте имеются транспортные средства в количестве d грузоподъемностью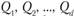 
Известно также расстояние перевозки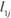 
между потребителями.
При решении задачи необходимо учитывать, что количество транспортных средств d должно быть больше,чем пунктов потребления n(d > п); в начальном пункте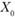 
(склад) количество продукции должно быть больше или равно сумме потребностей всех потребителей 
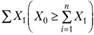. Каждый пункт потребления обслуживается подвижным составом одного типа (автомобиль грузоподъемностью 2,5 т); груз 2-го класса;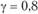
Для каждой пары пунктов (
) определяем расстояние перевозки 
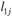. Это расстояние должно быть больше или равно нулю, т.е. 
.
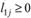Схема размещения пунктов и расстояния между ними приведены па рис. 5.11.
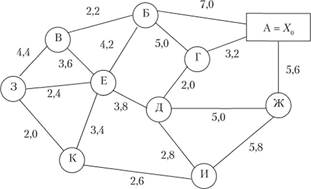
Рис. 5.11. Схема размещения пунктов и расстояния между ними
Требуется найти т замкнутых путей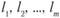 
из единственной общей точки 
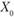так, чтобы выполнялось условие
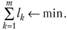
Решение.
Этап I. Строим кратчайшую сеть, связывающую все пункты без замкнутых контуров ("минимальное дерево") (рис. 5.12).
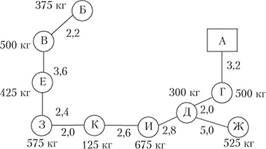
Рис. 5.12. Кратчайшая связывающая сеть ("минимальное дерево")
Затем по каждой ветви сети, начиная с пункта, наиболее удаленного от начального пункта А (считая по кратчайшей связывающей сети), группируем пункты на маршрут с учетом количества ввозимого груза и грузоподъемности единицы подвижного состава. Ближайшие к другой ветви пункты группируем вместе с пунктами данной ветви.
Исходя из данной грузоподъемности подвижного состава все пункты можно сгруппировать так, как показано в табл. 5.15.
Таблица 5.15
Группировка маршрутов исходя из грузоподъемности автомобиля
|
Маршрут I |
Маршрут II |
||
|
Пункт |
Объем завоза, кг |
Пункт |
Объем завоза, кг |
|
Б |
375 |
Ж |
525 |
|
В |
500 |
Д |
300 |
|
Е |
425 |
И |
675 |
|
3 |
575 |
Г |
500 |
|
К |
125 |
- |
- |
|
Всего |
2000 |
Всего |
2000 |
Сгруппировав пункты по маршрутам, переходим к следующему этапу расчетов.
Этап II. Определяем рациональный порядок объезда пунктов каждого маршрута. Для этого строим таблицу-матрицу
(табл. 5.16), в которой по диагонали размещаем пункты, включаемые в маршрут, и начальный пункт А, а в соответствующих клетках – кратчайшие расстояния между ними. Для примера матрица принята симметричной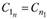
, хотя
приведенный ниже способ применим для решения и несимметричных матриц.
Таблица 5.16
Матрица для определения рационального порядка объезда пунктов
|
Номер строки |
А |
7,0 |
9,2 |
9,0 |
11,4 |
10.6 |
|
1 |
7,0 |
Б |
2,2 |
4,2 |
6,6 |
7,6 |
|
2 |
9,2 |
2,2 |
В |
3,6 |
4,4 |
6,4 |
|
3 |
9,0 |
4,2 |
3,6 |
Е |
2,4 |
3,4 |
|
4 |
11,4 |
6,6 |
4,4 |
2,4 |
3 |
2,0 |
|
5 |
10,6 |
7,6 |
6,4 |
3,4 |
2,0 |
К |
|
Σ |
47,2 |
27,6 |
25,8 |
22,6 |
26,8 |
30,0 |
Начальный маршрут строим для трех пунктов матрицы, имеющих наибольшие размеры сумм, показанных в строке (47,2; 30,0; 27,6), т.е. А; К; Б. Для включения последующих пунктов выбираем из оставшихся пункт, имеющий небольшую сумму, например пункт 3 (сумма 26,8), и решаем, между какими пунктами его следует включать, т.е. между А и К, К и Б или Б и А.
Чтобы решить данную подзадачу, для каждой пары пунктов необходимо найти размер приращения маршрута по формуле
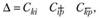
где С – расстояние, км; i – индекс включаемого пункта; k – индекс первого пункта из пары; р – индекс второго пункта из пары.
При включении пункта 3 между первой парой пунктов А и К определяем размер приращения ΔΑΚ при условии, что i = 3; k = А; р = К. Тогда
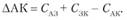
Подставляем значения из табл. 5.16. Получаем, что ΔАК= 11,4 + 2,0-10,6 = 2,8 км.
Таким же образом определяем приращение АКБ (если пункт 3 включить между пунктами Б и А), км:
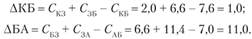
Из полученных значений выбираем минимальное, т.е. АКБ = 1,0.'
Следовательно, пункт 3 должен быть между пунктами К и Б. Получаем маршрут вида A – К – 3 – Б – A.
Используя этот метод и формулу приращения, определяем между какими пунктами следует расположить пункты В и Е. Начнем с пункта В, так как размер суммы (см. табл. 5.15) этого пункта больше (25,8 > 22,6). Итак, приращение, км, равно:
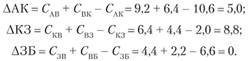
В том случае, когда А = 0, для симметричной матрицы расчеты можно не продолжать, так как значение, меньшее, чем 0, получено быть не может. Поэтому пункт В должен быть между пунктами 3 и Б. Тогда маршрут получит следующий вид: А–К–З–В–Б–А.
В результате проведенного расчета включаем следующий пункт Е между пунктами 3 и В, так как для этих пунктов получено минимальное приращение 1,6:
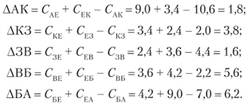
Таким образом, окончательный порядок движения по маршруту I будет следующим:
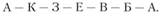
Таким же методом определяем кратчайший путь объезда пунктов по маршруту II. В результате расчетов получим маршрут
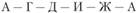длиной 19,4 км.
Порядок движения по маршрутам I и II приведен на рис. 5.13.
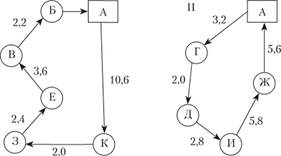
Рис. 5.13. Порядок движения по маршрутам I и II
Логистическая система может заниматься и прикреплением поставщиков к потребителям. Это возможно при наличии у поставщика региональных складов, находящихся в различных экономических районах, и определенного количества потребителей.
Оптимальное прикрепление потребителей к региональным складам с применением методов линейного программирования логистические подразделения осуществляют в виде решения транспортной задачи. Для составления экономико-математической модели необходимо знать ряд данных: потребности потребителей, ресурсы поставщиков, транспортные расходы на перевозку продукции и некоторые другие. После этого формулируется постановка задачи и составляется экономико-математическая модель.
Постановка задачи. Имеется т поставщиков[1], располагающих определенным количеством продукции, и п потребителей, у которых есть потребность на данную продукцию. Известны транспортные расходы по доставке единицы продукции от любого поставщика до любого потребителя. Требуется прикрепить потребителей к поставщикам так, чтобы суммарные транспортные расходы по доставке всей продукции потребителям были минимальными.
Для построения экономико-математической модели вводятся следующие обозначения:
i – номер (индекс) поставщика (i = 1, 2, т); пусть т = 4, т.е. имеются четыре поставщика (i = 1, 2, 3, 4);
Аi – ресурсы i-го поставщика (i = 1, 2, 3, 4), т.е. количество продукции, которое поставщик может отправить потребителям; пусть A1 = 160 т, А2 = 240 т, А3 = 100 т, А4 = 200 т, а всего – 700 т;
у – номер (индекс) потребителя (j = 1, 2,..., гг); пусть п = 5, тогда (j= 1, 2, 3, 4, 5);
Bj – потребность в продукции j-го потребителя; пусть B1 = 150 т, В2 = 180 т, B3 = 200 т, В4 = 120 т, B5 = 50 т, а всего – 700 т;
Сij – транспортные расходы по доставке единицы продукции от i-го поставщика j-му потребителю. Транспортные расходы для числового примера заданы в табл. 5.17.
Таблица 5.17
Транспортные расходы по доставке единицы продукции i-го поставщика j-му потребителю
|
Поставщик |
Потребитель |
||||
|
j=l |
j = 2 |
j = 3 |
j = 4 |
j = 5 |
|
|
i = 1 |
|
|
|
|
|
|
i = 2 |
|
|
|
|
|
|
i = 3 |
|
|
|
|
|
|
i = 4 |
|
|
|
|
|
Xij – количество продукции, поставляемой от i-го постав- щи кау-му потребителю; эта величина неизвестна и подлежит определению; в процессе решения задачи должны быть найдены все значения Xij, указанные в табл. 5.18.
После введения обозначений и принятия числовых значений (ресурсы поставщиков, потребность потребителей и транспортных расходов по доставке продукции) составим табл. 5.19. Укажем в ней исходные данные для решения экономико-математической модели: ресурсы поставщиков, потребности потребителей и транспортные расходы (они проставлены в выделенных прямоугольниках). Кроме того, в табл. 5.19 предусмотрен столбец для записи потенциалов Ui и Vj.
Таблица 5.18
Матрица решений
|
Поставщик |
Потребитель |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.19
Исходные данные для оптимального решения прикрепления потребителей к поставщикам
|
Поставщик |
Потребитель |
Ресурсы постав щиков |
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
160 |
|
|
|
|
|
|
|
|
240 |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
200 |
|
Потребности потребителей |
150 |
180 |
200 |
120 |
50 |
700 |
|
Приступим к построению модели. Экономико-математическая модель оптимального прикрепления содержит целевую функцию, системы ограничений (определенные условия) и условия неотрицательности переменных.
В рассматриваемой модели ставится задача свести к минимуму транспортные расходы.
Для нашего числового примера (см. табл. 5.11) целевая функция будет иметь следующий вид:
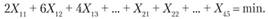
В общем виде целевая функция выглядит следующим образом:
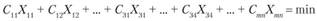
или
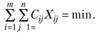(5.19)
Достижение минимального значения целевой функции должно происходить при определенных условиях. Первое из них состоит в том, что по оптимальному варианту от каждого поставщика планировалось к поставке то количество продукции, которым он располагает. Это условие для рассматриваемого примера записывается в виде системы уравнений.
В общем виде система уравнений для первого условия записывается так:
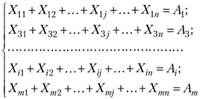
или
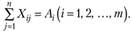(5.20)
Для числового примера (см. табл. 5.11):
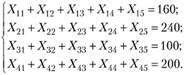
Наконец, в модели указывается присущее многим моделям условие неотрицательности переменных, т.е. значение переменной (поставки) должно быть равно или больше нуля, так как отрицательное значение поставки не имеет смысла:
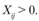(5.21)
Таким образом, экономико-математическая модель оптимального прикрепления потребителей к поставщикам будет иметь следующий вид:
при условиях:
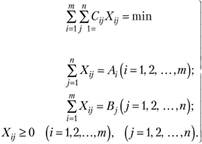(5.22)
Приведенная модель соответствует закрытой модели, так как
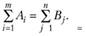
Если же условия равенства ресурсов и потребности нет, т.е.
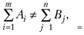
то строится открытая модель.
После построения экономико-математической модели решается задача прикрепления поставщиков к потребителям. Расчеты выполняют в специальной таблице (матрице) линейного программирования методом потенциалов (см. табл. 5.18). В этой таблице, кроме ресурсов поставщиков, потребностей потребителей и транспортных расходов, имеются столбец и строка для записи потенциалов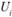 
и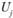 
, которые дают возможность определить оптимальность плана закрепления поставщиков за потребителями.
Решение.
Решение задачи начинается с построения исходного плана
Метод потенциалов, как и другие методы линейного программирования, требует, чтобы исходный вариант и все последующие варианты удовлетворяли следующим условиям:
1) число загруженных клеток X в таблице должно быть на единицу меньше суммы чисел поставщиков (т) и числа потребителей (n); в нашем примере это число должно быть равно 8, т.е. т + п – 1=4 + 5- 1=8;
2) не должно быть ни одного занятого квадрата, который оказался бы единственным в строке и в столбце таблицы;
3) занятые квадраты таблицы должны быть расположены так, чтобы можно было образовать так называемую вычеркиваемую систему.
Для составления исходного плана воспользуемся приемом, который называется "метод северо-западного угла". Согласно этому методу заполнение таблицы прикрепления следует начать с левого верхнего квадрата и с позиции этого квадрата сравнить ресурсы первого поставщика (160 т) и потребности первого потребителя (150 т), выбрать меньшее значение из них и записать в данный квадрат, который с этого момента становится "загруженным" (табл. 5.20).
В нашем примере записано значение "150", равное потребности первого потребителя. Затем необходимо подвинуться вправо от северо-западного угла и сравнить остав-
Таблица 5.20
Исходный план прикрепления потребителей к поставщикам
|
Поставщик |
Потребитель |
Ресурсы поставщиков |
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
160 |
|
|
|
|
|
|
|
|
240 |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
200 |
|
Потребности потребителей |
150 |
180 |
200 |
120 |
50 |
700 |
|
шиеся ресурсы первого поставщика. Они составили 10 т (160 – 150 = 10). Их мы записываем второму потребителю и делаем вывод: мы полностью использовали ресурсы первого поставщика и удовлетворили потребности первого потребителя. Перемещаемся ниже ко второму потребителю. Он имеет 10 т ресурсов от первого поставщика. Чтобы удовлетворить его потребность, берем 170 т у второго поставщика (всего у него 240 т, см. табл. 5.20). После этого действия мы удовлетворяем потребности второго потребителя (10 + 170 = 180), а 70 т переместили третьему потребителю. Далее действуем по отработанной схеме.
Двигаясь шаг за шагом, получаем исходный план (см. табл. 5.20). Определим значение некоторых цифр, содержащихся в таблице. Числа, выделенные в таблице, – это количество продукции, которое по исходному плану намечено к поставке. Квадраты, в которых расположены эти цифры, называются "загруженными"; квадраты, не содержащие поставок, – "свободными".
Числа, расположенные в свободных квадратах таблицы, являются вспомогательными и представляют собой сумму соответствующих условных величин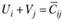 
(потенциалов). Для загруженных квадратов суммы
+
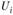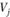должны совпадать с транспортными издержками 
.
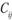После составления исходного плана проверим условие т + п – 1=8, т.е. необходимо иметь 8 загруженных клеток, что мы и имеем.
По исходному варианту транспортные расходы, руб., составят:
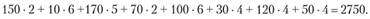
Вперед стадия заключается в проверке исходного плана на оптимальность. Для этого необходимо определить индексы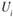 
и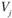 
. Индексы определяются для загруженных клеток. Сумма индексов 
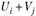должна быть равна транспортным издержкам 
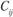, т.е. 
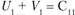, и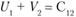 
и т.д. В нашем примере значения U. и V. должны быть такими, чтобы 
; 
; 
; 
; 
; 
; 
; 
.
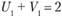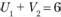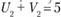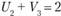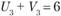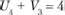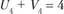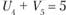Индексы определяем следующим образом. Принимаем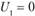 
. Так как 
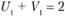, то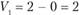 
Аналогично определяем значение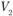 
. Так как 
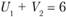, то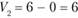 
Далее определяем индекс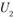 
. Так как 
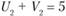, а 
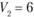, то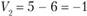 
.
Теперь можно определить индекс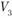 
. Исходя из того, что 
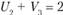, его значение 
Продвигаясь подобным образом последовательно по всем загруженным квадратам, нетрудно определить псе значения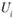 
и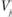 
.
Далее исчисляем значения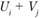 
в незагруженных клетках и записываем в свободные квадраты. Например: 
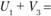= 0 + 3 = 3; 
; 
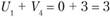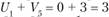и т.д.
Записанные значения сумм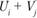
в свободных квадратах 
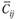как правило, отличаются от значений 
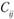(транспортные издержки).
При этом возможны три случая:
1) 
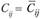; 2) 
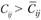; 3)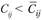 
.
Сравниваем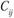 
и 
и 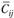определяем, является ли полученный вариант прикрепления потребителей к поставщикам, оптимальным. Если для всех свободных квадратов оказывается, что 
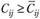, то план считается оптимальным. Если хотя бы в одном из квадратов это условие не соблюдено, считается, что план нс является оптимальным и его можно улучшить. В нашем примере (табл. 5.20) план не является оптимальным, так как 
, 
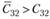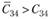. Следовательно, его можно улучшить.
Улучшают вариант путем перемещения поставки в "свободные" квадраты, для которых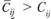
. Если имеется
несколько свободных квадратов, необходимо осуществлять перемещение для той, у которой Сj > Сi = max. В нашем примере этот квадрат расположен в третьей строке второго столбца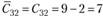 
. В другом квадрате эта разность меньше (
).
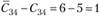В том случае, если разность окажется одинакова для сравниваемых свободных квадратов, следует выбирать один из них произвольно.
Итак, в рассматриваемом примере поставка должна быть перемещена в квадрат третьей строки и второго столбца. Перемещения производятся в определенном порядке с тем, чтобы нс были нарушены условия, выраженные в приведенных выше уравнениях. Для этого образуем связку, т.е.
замкнутую ломаную линию, состоящую из горизонтальных и вертикальных отрезков, таким образом, чтобы одной из вершин образованного многоугольника был сам свободный квадрат, а остальные вершины находились бы в занятых квадратах.
Свободный квадрат может быть соединен четырьмя прямыми отрезками с соседними занятыми квадратами, как это показано ниже.
II столбец
III столбец
II строка
III строка
После образования связи свободному квадрату и связанным с ним загруженным квадратам присваиваем поочередно знаки "-" или "+", начиная со свободного квадрата. В приведенном выше примере показана расстановка знаков. Направление расстановки знаков безразлично.
Далее просматриваем те занятые квадраты, которым присвоен знак "+", и выбираем тот из них, в котором содержится наименьшая поставка, в рассматриваемом примере она равна 100 т. Именно это значение подлежит перемещению из каждого квадрата со знакам "+" в каждый квадрат (в том числе и свободный) со знаком "-". Перемещение выглядит так:
|
70 |
170 |
|
100 |
Свободный |
В результате перемещения получаем новый вариант прикрепления (табл. 5.21).
Транспортные расходы составляют 2050 руб., т.е. они на 700 руб. меньше, чем в исходном варианте.
Законченный цикл вычислений, приводящих к получению нового варианта, называется вычислением отдельных итераций.
В отношении полученного варианта прикрепления поступают точно так же, как и в отношении исходного варианта, т.е. вычисление очередной итерации производят в следующем порядке:
1) определяют потенциалы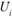 
и 
для загруженных клеток;
2) исчисляют значения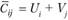 
для свободных клеток;
3) сопоставляют значения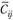 
и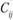 
.
Таблица 5.21
Оптимальный план прикрепления потребителей к поставщикам
|
Поставщик |
Потребитель |
Ресурсы поставщиков |
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
160 |
|
|
|
|
|
|
|
|
240 |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
200 |
|
Потребности потребителей |
150 |
180 |
200 |
120 |
50 |
700 |
|
Если находят план неоптимальным, то производят вычисления вновь для условий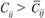 
.
Расчеты для рассматриваемого примера приведены в табл. 5.21. Условие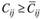 
обеспечивается для всех свободных квадратов, причем в одномслучае (квадрат первого столбца четвертой строки 
) 
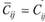. Это означает возможность получения другого равноценного оптимального варианта.