Висновки

Клас

І.

1. За означенням , , ,тоді . Чи завжди можлива ця дія, якщо і ?

Ні, тільки тоді, якщо і . Таке обмеження створює незручності при алгебраїчних перетвореннях, бо оперуючи з буквеними показниками треба, щоразу враховувати, що перетворення частки степенів справедливе лише при . Цю незручність можна усунути розширивши поняття про степінь у 8 класі, таким чином, щоб властивості степеня з натуральним показником збереглися.

Клас

Вводиться поняття степеня з цілим показником у такому порядку:

а) вводять степінь з нульовим показником

б)степінь з цілим від’ємним показником, щоб правило ділення степенів однієї основи можна було застосувати для випадку, коли .

; . Але виявилось, що у такому випадку слід обмежити основу ; ; бо вираз не має змісту.

Клас

Степінь з раціональним показником. Означення степеня з дробовим показником має бути таким, щоб властивості степеня з натуральним показником залишилися правильними.

Це означення виникло у зв’язку з бажанням узагальнити правило добування кореня у випадку, коли показник підкореневого виразу не ділиться на показник кореня. Правило було виведене з припущення, що і і ділиться на 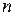. Тепер це правило треба вміти застосовувати і тоді коли , . Тут потрібно обмежити основу , бо не має змісту.

Пропонуємо учням за допомогою калькулятора обчислити значення виразів: а) , б) .

Виникає запитання: а як розуміти вирази , , .

 

Узагальнення поняття степеня

1. Степінь з натуральним показником

,

а – основа степеня,

n – його показник

2. Степінь з цілим показником

,

1. ,

2.

3. , ,

3. Степінь з раціональним показником і , де , , де ,

, , , ,

1. Якщо , то

2.

 

Узагальнення поняття степеня
Степінь з натуральним показником	Степінь з цілим показником	Степінь з раціональним показником і , де , , де ,
, , 1. 2. 3. при ; 4. 5. 6. ,	, , 1. 2. 3. , при 4. 5. 6. , 7. 8. Якщо і , то 9. Якщо і то	, , , якщо , , якщо , якщо , , якщо , , якщо ,

 

 

5. Методика введення степеня з ірраціональним показником.

П р о п о н у є м о у ч н я м:

Обчислити значення виразів:

а) ; б) ; в) , де – ірраціональне число.

Виникає потреба ввести означення степеня з ірраціональним показником , де - ірраціональне число.

Воно вимагає нової конструкції. При цьому бажано степінь з ірраціональним показником означити так, щоб зберегти всі відомі властивості степеня з раціональним показником. Така спадковість уже мала місце при переході від натурального показника до раціонального. Проведемо деякі міркування.

Розглянемо степінь , де - ірраціональне число, для якого існують дві послідовності раціональних чисел і взяті з недостачею і надлишком.

: 1; 1,4; 1,41; 1,414; ……

: 2; 1,5; 1,42; 1,415;…..

Тобто число запишемо:

…………………..

Утворимо нові послідовності відповідних значенню степеня числа 3.

; ; ; …..

; ; ;……..

За властивостями степеня з раціональним показником випливає, що:

а) ; б) ; в) ,

де =0, 1, 2, …..

можна довести, що існує єдине число, яке при будь-якому = 0, 1, 2, 3... більше і менше . Це число . Існування такого числа можна показати геометрично:

 

Аналогічно міркують і для чисел , яке більше і менше при = 0, 1, 2...

Таким чином, степінь числа , з показником означається так:

1. Якщо , то - степінь з цілим показником.

2. Якщо , то - степінь з раціональним показником.

3. Якщо , то:

а) при , число - означає таке число, яке більше і менше ( 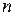=0, 2, 3, ….)

б) при ; ( 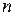=0, 1, 2, ….)

в) при ;

4. Якщо , то

Наприклад, .

Існування і єдність числа доводиться у курсі математичного аналізу. Властивості степеня з ірраціональним показником приймаються без доведення.

Дії над степенями з ірраціональним показниками виконуються за зразками (правилами), які встановлено для степенів з раціональними показниками. Степінь з ірраціональним показником зберігає всі властивості степеня з раціональним показником. У класах з поглибленим вивченням математики, де учні знайомі з поняттям границі числової послідовності, можна сформулювати означення з степеня з ірраціональним показником так:

 

Вправи на закріплення:

1. Обчисліть: а) ; б) ; в) ; г) .

2. Порівняйте числа: а) і ; б) і

3. Спростіть вираз: ; ; .

4. За допомогою мікрокалькулятора обчисліть з точністю до 0,001 значення:

а) ;

б) ;

в) ;

Маючи результати, знайдіть значення з точністю до 0,01.

Степенева функція, властивості та її графік.

Означення: функція виду , де х – незалежна змінна, а називається степеневою функцією.

Властивості функції

( – натуральний показник)

1. Область визначення

,

2. Область значень

3.

4.

---

5. Парна так ні

Непарна ні так

6. Монотонність

зростає

спадає ------

7. Найбільше та найменше немає

значення немає

Г Р А Ф І К И

непарне натуральне число:

- непарне від’ємне число

 

- парне від’ємне число

- неціле додатне число

 

7. Методика введення показникової функції

а) Методичні особливості вивчення показникової функції

На її вивчення відводиться 20 год (8 год резерв), які можна спланувати по різному. Один з можливих варіантів :

1. На вивчення теоретичного матеріалу – 4 год. Його можна провести у вигляді уроків-лекцій.

2. На закріплення знань, формування вмінь та навичок –14 год. Тут можна використати уроки різних видів:

- уроки розв’язування типових (ключових) завдань;

- уроки-практикуми;

- уроки – семінари та інші нетрадиційні уроки;

3. Для тематичного контролю і корекції знань – 2 год.

Основна мета вивчення теми:

- ввести означення показникової та степеневої функції;

- розглянути їх графіки і властивості;

- розглянути показникових та степеневих рівнянь і нерівностей (та їх системи).

В результаті вивчення теми учень повинен знати :

- означення показникової та степеневої функції;

- основні показникові та степеневі властивості;

- означення показникових та степеневих рівнянь.

В м і т и:

- будувати ескізи, графіки показникових та степеневих функцій і “читати” за графіками властивості функцій;

- спрощувати показникові та степеневі вирази;

- розв’язувати показникові рівняння та нерівності.

Для вивчення теми можуть бути обрані:

пояснювально-ілюстративний, репродуктивні методи, у деяких випадках метод проблемного вивчення матеріалу (наприклад, під час побудови графіків функцій ; ). Методи наукового пізнання: аналіз; синтез ; аналогія; порівняння; спостереження узагальнення. У класах з поглибленим вивченням математики: дослідницький, частково-пошуковий, самостійні роботи, роботи з підручником, творчі самостійні роботи.

Під час вивчення “Показникової та степеневої функції” доцільно поєднати аналітичний та графічний методи, подбати, щоб учні добре усвідомили взаємозв’язок між прямою та оберненою функціями. Тоді на основі властивостей показникової функції можна вивчити властивості логарифмічної. Такий підхід заощадить час і сприятиме кращому усвідомленню властивостей двох взаємно обернених функцій. Відповідно до цього доцільно розглядати матеріал теми у такій послідовності:

1. Поняття про степінь з ірраціональним показником.

2. Означення та властивості показникової функції.

3. Показникові рівняння і нерівності.

4. Поняття про логарифми.

5. Логарифмічна функція, як обернена до показникової.

6. Логарифмічні рівняння та нерівності.

До засобів навчання можна віднести перш за все:

- систему вправ, запитань, задач.

Ця система вправ і задач може виступати як засіб навчання і як метод навчання.

Наприклад: чи можна побудувати графік функцій маючи графік функції і т.д.

- таблиці з графіками, кольорова крейда, кадескоп, ще краще комп’ютер, калькулятор для обчислення степенів з раціональним показником виду , , ;

-дидактичний роздатковий матеріал, різних рівнів складності.

Під час вивчення теми можна використати різні форми навчальної діяльності учнів, а саме: фронтальну, групову, парну, індивідуальну. Таким чином, вчитель враховуючи зміст навчального матеріалу, математичну підготовку учнів, та свої особисті якості повинен вибрати найбільш раціональні методи, форми та засоби навчання, щоб забезпечити виконання мети навчання.

 

б) Мотивація вивчення показникової функції

Сьогодні багато говорять про інформаційний багажник. Стверджують, що кількість інформації подвоюється кожні десять років, зобразимо це у вигляді графіка деякої функції. Візьмемо обсяг інформації у деякий початковий рік за 1. Удвічі більший відрізок поставимо над одиничною оцінкою, вважаючи, що оцінка відповнюється першому десятку років. Удвічі більший відрізок відповідає другому десятку років і т.д.

Обрані нами значення аргументу є елементами арифметичної прогресії 1, 2, 3, . . . .А значення функції зростають за законом геометричної прогресії 2, 4, 8, . . . Побудуємо графік функції.

Перед нами графік показникової функції. Головна особливість цієї функції – крутизна. Показникові функція зустрічається в описі процесів, у яких швидкість зміни величини пропорційна до самої величини. За таким правилом розмножується все живе. За законом експоненціального зростання збільшується колонія мікробів у чашці Петрі. За таким законом плодилися кролі, які за короткий термін заполонили Австралію. Прикладом показникового спадання є хід хімічної реакції. Швидкість хімічної реакції пропорційна до кількості речовин, що реагують. Швидкість радіоактивного розпаду пропорційна до кількості атомів, що не розпалися.

Задача

У деякій культурі через два дні утворюється 370000 бактерій, через 5 днів – 5310100. Скільки їх було спочатку, через 1 день, через 3 дні.

370 000 =

5 310 000 =

в) Деякі задачі, що приводять до поняття показникової функції

Спочатку розглянемо конкретні приклади функціональних залежностей, які ілюструють використання показникової функції для опису різних явищ природи.

Задача. Державні ощадкаси нараховують вкладникам по 9% за термін вкладання. Вкладник 1.01.98р. поклав у ощадкасу 500 гривень. Яку суму становитиме його вклад через 10 років ?

Розв’язання

Розв’яжемо цю задачу у загальному вигляді. Нехай вклад на 1.01.98 становить а гривень, тоді 1.01.1999р. каса нараховує 9%=0,009 від суми а гривень і його вклад становитиме (а+0,09а) гривень або 1,09а гривень.

На 1.01.2000р. гривень. Міркуючи так і дальше, знайдемо, що розміри вкладів утворюють геометричну прогресію , , , ….. із знаменником .

Через повних років вклад становить

Наведемо конкретні приклади функціональних залежностей (про зміну атмосферного тиску)

Приклад 1

Атмосферний тиск зміниться в залежності від висоти над рівнем моря за законом , де - атмосферний тиск на рівні моря (7600), а – деяка стала.

Приклад 2

Дерево росте так, що кількість деревини збільшується з часом за законом , де М- кількість деревини у даний момент, ( ).

М – початкова кількість деревини, - час (у роках ), який відлічують з моменту , - деяка стала. За скільки років об’єм деревини збільшиться в разів ?

Розв’язання

Якщо в даний момент , то поділивши обидві частини рівняння на дістанемо , , ,

Об’єм деревини збільшиться в а разів через років.

Приклад 3

Розмноження бактерій у певному середовищі відбуваються так, що їх число змінюється з часом за законом , де - початкове число бактерій при , і - деякі сталі.

У наведених прикладах для обчислення кожного значення функції певне число а, одне і те саме на протязі всього процесу доводиться підносити до деякого степеня. Найпростішим випадком цієї залежності є функція , де а – додатне дійсне число, х – залежна змінна, що набуває будь-яких дійсних значень. Очевидно, вона має свою назву. Оскільки показником є змінна величина, то функція називається показниковою.

1. При , а х – раціональне, знаменник, якого парне число, вираз не має смислу.

Наприклад: , у множинах дійсних чисел не має смислу.

2. , , степінь існує.

Але при , , степінь - не має смислу.

Наприклад: ;

3. При , степінь або , така функція існує, відноситься до лінійних. Вона є сталою і не становить інтересу. Тому значення виключають у розгляду.

Таким чином, формулюємо означення показникової функції. Функція , яку можна задати рівністю , де , , називається показниковою.

г) Властивості показникової функції

У шкільній практиці існує 2 підходи до вивчення властивостей показникової функції.

a. Спочатку доводять аналітично всі властивості, а потім розглядається функція при конкретному значенні а і будується графік. Такий підхід був обраний у підручнику алгебри Кисельова. Він виявився важким для сприймання учнями, тобто це є дедуктивний метод.

b. За точками ( за допомогою заздалегідь складеної на дошці таблиці, або фабричної) , будуються графіки певних показникових функцій.

Наприклад: ; ; ; і за графіком з’ясовують властивості функції при та , а потім ці властивості доводять аналітично. Такий підхід прийнятий у більшості підручників та посібників у тому числі і діючому підручнику з алгебри та початків аналізу. Учитель вказує, що при вивченні властивостей показникової функції заслуговують на увагу два істотних випадки:

1. Основа а є неправильним дробом тобто

2. Основа а – правильний дріб

При цьому підкреслюється уже відоме твердження.

1. Додатний степінь неправильного дробу більший від 1;

Наприклад .

Від’ємний степінь неправильного дробу менший від 1

Далі будуємо графік функції .

	-3	-2,5	-2	-1,5	-1	-0,5		0,5		1,5
	0,125	0,177	0,25	0,354	0,5	0,707		1,414		2,828

 

 

Складаємо таблицю значень аргументу і відповідних значень функцій:

	-4	-3	-2	-1

 

 

 

Будуємо графіки, сполучаємо плавною лінією.

Розглянемо функцію . Складаємо аналогічно таблицю:

	-3	-2	-1

 

Будуємо графік функції

 

	-4	-3	-2	-1

Розглядаючи графіки функцій вияснимо, що спільного у графіків функцій і

1) Область визначення обох функцій є

2) Обидві функції додатні при будь-якому х.

При х=0 обидві функції набувають значень, що дорівнює 1.

Далі будуємо графік функцій і в одній системі координат і порівнюємо їх властивості:

1) Графіки розміщені симетрично відносно осі ординат.

2) - зростає, - спадає.

3) При набуває значень

при , а при .

 

Властивості функції при і при суттєво відрізняються.

Тому спочатку розглянемо загальні властивості показникової функції, а потім окремо для і .

1. Область визначення є множина , бо при , вираз - визначений для будь-якого .

2.Показникова функція при будь-якому додатна, тобто . Справді може дорівнювати нулю лише тоді, коли . Але ми домовляємося, що .

Функція може бути від’ємною лише при ( ). Але ми домовимося розглядати показникові функцію лише при . А при піднесенні додатного числа до степеня , де завжди матимемо додатне число. Щоб переконатися в цьому розглянемо чотири випадки:

а ) Нехай , де . Тоді

як добуток додатних чисел.

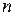
б )Якщо х – раціональне додатне число, тобто , де - нескоротний дріб і , то .

Але ( умова існування кореня 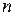- го степеня, або значення степеня з додатним раціональним показником, тому .

в) Нехай – додатне ірраціональне додатне число. Позначимо через і наближені (раціональні додатні значення з недостачею і надлишком. Тоді значення міститься між двома додатними числами і , , отже .

г ) Якщо х – деяке від’ємне число:

наприклад: , то . Але у пункті показано, що при будь-якому додатному раціональному . Отже, , а значить , отже, графік показникової функції завжди лежить над віссю абсцис і не перетинає її ( ).

3⁰. При х = 0 показникова функція . Це випливає з того, що будь-яке число відмінне від нуля у нульовому степені дорівнює одиниці. А ми домовимося розглядати функцію для . Звідси висновок, що графік функції проходить через точку (0; 1) тобто перетворює вісь ординат на відстані одиниці від початку координат.

Ці три властивості спільні для будь-яких показникових функцій.

4⁰. При , , якщо і

, якщо ;

При , , якщо

, якщо .

Доведення

1. Доведемо цю властивість для .

а) Якщо , , тоді

б) Якщо ( і ) , тоді

 

За доведеним вище ;

Тоді , тобто , а значить .

в) – ірраціональне додатне число.

За означенням степеня з додатного ірраціонального показника при маємо , , а значить .

г) Якщо – будь-яке від’ємне дійсне число.

Нехай , де . бо за доведенням .

5⁰. При функція монотонно зростає, - монотонно спадає.

Доведення

1) . Візьмемо два значення і при чому .

Доведемо, що

Порівняємо і для цього застосовуємо різницю .

а) За властивістю 1^{0 .}

б) За умови тому , а значить за властивістю 2⁰.

Отже, , а значить добуток тобто

Проектуємо на екран малюнок на якому зображені графіки показникової функцій при різних параметрах

Зауважимо, що для всіх функцій графіки яких зображено на малюнку є спільні властивості.

1)

2)

3)

 

д) Вправи для закріплення властивостей показникової функції

1. Якщо графіки функцій і симетричні відносно осі ординат, то яке співвідношення існує між і ?

2. Чи мають спільну точку графіки і ?

3. у якій точці перетинаються графік функції з віссю ординат?

4. Які процеси в галузі техніки та природознавства виражають за допомогою показникової функції ?

5. Які з функції ; ; ; ; – є показниковими.?

6. За яких умов ; ?

7. Яка особливість розміщення графіків функцій ; ; ; ?

8. Відомо, що . Що більше чи при ?

9. Порівняйте і , якщо відомо, що і .

10. Чи правильно є нерівність при ?

11. Які з показникових функцій ; ; ;