Приложение дифференциального исчисления к исследованию функции
Пусть дана функция одной переменной 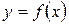 .
.
Требуется исследовать ее методами дифференциального исчисления и построить ее график.
Для решения этой задачи рекомендуется следующая схема:
1) Найти область определения функции.
2) Исследовать функцию на четность и периодичность.
Указать симметрию графика функции относительно оси ординат, либо начала координат, если она имеет место.
3) Исследовать функцию на непрерывность, найти точки разрыва функции (если они имеются), указать их характер, исследовать поведение функции вблизи точек разрыва.
4) Найти асимптоты графика функции (если они имеются).
5) Найти точки пересечения графика функции с осями координат (если они имеются), указать интервалы знакопостоянства функции.
6) Найти точки экстремума, экстремумы функции (если они имеются), указать интервалы монотонности.
7) Найти точки перегиба графика функции (если они имеются), указать интервалы выпуклости и вогнутости.
8) Найти несколько дополнительных точек (если это необходимо) и построить график функции, пользуясь результатами проведенного исследования.
Определение.Интервалы, в которых функция только возрастает или только убывает, называются интервалами монотонности функции.
Отметим необходимые и достаточные условия возрастания и убывания функций.
Теорема 6.8 (необходимые условия). Если дифференцируемая на интервале  функция
функция  возрастает (убывает), то
возрастает (убывает), то  для любого
для любого  .
.
Теорема 6.9(достаточные условия). Если функция  дифференцируема на интервале
дифференцируема на интервале  и
и  для любого
для любого  , то эта функция возрастает (убывает) на интервале
, то эта функция возрастает (убывает) на интервале  .
.
Определение.Точка  называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции  , если существует
, если существует  -окрестность точки
-окрестность точки  такая, что для всех
такая, что для всех  этой окрестности выполняется неравенство:
этой окрестности выполняется неравенство: 
 .
.
Значение  называют максимумом (минимумом) функции.
называют максимумом (минимумом) функции.
Определение.Точки максимума или минимума функции называют точками экстремума функции.
Экстремумы функции носят локальный характер – это наибольшее или наименьшее значения функции по сравнению с близлежащими ее значениями (рисунок 5 и рисунок 6)
 |


Рисунок 5 Рисунок 6
Теорема 6.10(необходимое условие экстремума). Если дифференцируемая функция 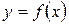 имеет экстремум в точке
имеет экстремум в точке  , то ее производная в этой точке равна нулю:
, то ее производная в этой точке равна нулю:  .
.
Замечание. 1) Если  , то это не значит, что
, то это не значит, что  – точка экстремума. 2) Существуют функции, которые в точках экстремума не имеют производной.
– точка экстремума. 2) Существуют функции, которые в точках экстремума не имеют производной.
Например, непрерывная функция  в точке
в точке  не имеет производной, но точка
не имеет производной, но точка  – точка минимума этой.
– точка минимума этой.
Определение.Непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются критическими.
 Если производная в какой-либо точке равна нулю или не существует, то это не значит, что в ней функция будет иметь экстремум. В этом можно убедиться на следующем примере.
Если производная в какой-либо точке равна нулю или не существует, то это не значит, что в ней функция будет иметь экстремум. В этом можно убедиться на следующем примере.
Например, для функции  при
при  производная не существует:
производная не существует:  . Экстремума нет (рисунок 7).
. Экстремума нет (рисунок 7).
Экстремальные точки относятся к критическим, но не исчерпывают их, а являются только частью критических точек. Поэтому по необходимому признаку нельзя установить наличие экстремума функции в данной точке.
Теорема 6.11(достаточное условие экстремума). Если непрерывная функция  дифференцируема в некоторой
дифференцируема в некоторой  -окрестности критической точки
-окрестности критической точки  и при переходе через нее (слева направо) производная
и при переходе через нее (слева направо) производная  меняет знак с плюса на минус, то
меняет знак с плюса на минус, то  есть точка максимума; с минуса на плюс, то
есть точка максимума; с минуса на плюс, то  – точка минимума.
– точка минимума.
Итак, чтобы найти экстремальные точки функции одного переменного необходимо:
1) найти ее первую производную;
2) определить критические точки, т.е. найти значения аргумента, где первая производная равна нулю или не существует;
3) исследовать их на экстремум с помощью достаточного признака.
Иногда бывает удобным использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной.
Теорема 6.12 Если в точке  первая производная функции
первая производная функции  равна нулю
равна нулю  , а вторая производная в точке
, а вторая производная в точке  существует и отлична от нуля
существует и отлична от нуля  , то при
, то при  в точке
в точке  функция имеет максимум и минимум при
функция имеет максимум и минимум при  .
.
ПримерНайти экстремумы функции  .
.
Первая производная:
 .
.
Критические точки:
 .
.
Вторая производная в произвольной точке:
 .
.
Ее значение в критических точках:

 .
.
При  функция имеет максимум, при
функция имеет максимум, при  функция имеет минимум.
функция имеет минимум.
Замечание. График дифференцируемой на  функции
функции  не имеет изломов и заострений.
не имеет изломов и заострений.

Определение.График дифференцируемой функции  называется выпуклым на интервале
называется выпуклым на интервале  , если дуга кривой на этом интервале расположена ниже касательной, проведенной к графику функции в любой точке
, если дуга кривой на этом интервале расположена ниже касательной, проведенной к графику функции в любой точке  (рисунок 8), в противном случае график функции называется вогнутым на интервале
(рисунок 8), в противном случае график функции называется вогнутым на интервале  (рисунок 9)
(рисунок 9)
Определение.Точка графика непрерывной функции  , отделяющая его части разной выпуклости, называется точкой перегиба.
, отделяющая его части разной выпуклости, называется точкой перегиба.
Интервалы выпуклости вниз и вверх находят с помощью теоремы:
Теорема 6.13 Если функция  во всех точках интервала
во всех точках интервала  имеет отрицательную вторую производную, т.е.
имеет отрицательную вторую производную, т.е.  , то график функции в этом интервале выпуклый вверх. Если же
, то график функции в этом интервале выпуклый вверх. Если же  для любого
для любого  – график выпуклый вниз.
– график выпуклый вниз.
Точки перегиба графика функции находят с помощью следующей теоремы:
Теорема 6.14 (достаточное условие существование точек перегиба). Если вторая производная  при переходе через точку
при переходе через точку  , в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой
, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой  есть точка перегиба.
есть точка перегиба.
НапримерФункция  при
при  имеет точку перегиба (рисунок 10),
имеет точку перегиба (рисунок 10), 

Рисунок 10 Рисунок 11
где вторая производная равна  :
: 
 .
.
Обратное утверждение неверно, т.е. если в точке  вторая производная равна нулю или не существует, то это не значит, что в данной точке график функции будет иметь перегиб.
вторая производная равна нулю или не существует, то это не значит, что в данной точке график функции будет иметь перегиб.
Например, для функции  при
при  вторая производная обращается в нуль:
вторая производная обращается в нуль:  ,
,  . Однако здесь нет точки перегиба (см. рисунок 11).
. Однако здесь нет точки перегиба (см. рисунок 11).