Чисельне диференціювання

До чисельного диференціювання функцій вдаються тоді, коли функція задана таблично, а тому методи диференціального числення просто незастосовні, або коли функція задана досить складним аналітичним виразом і тому обчислення похідних пов’язане із значними труднощами, хоча для сучасних пакетів це не проблема. У цьому випадку користуються наближеним диференціюванням.

Практично усі формули наближеного диференціювання базуються на тому, що задану функцію 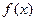на відрізку 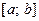, замінюють інтерполяційним поліномом . Тоді

, (1)

де – залишковий член інтерполяційної формули.

Якщо функція 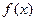на відрізку 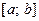має похідні до k-го, порядку включно, то, диференціюючи рівність (1) по x, знаходять:

………………….

За наближені значення похідних від функції 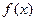беруть перші доданки правих частин наближених рівностей:

. (2)

Слід зауважити, що з малості залишкового члена інтерполяційної формули зовсім не випливає малість залишкового члена похідних. Наприклад, функції і для великих значень n можуть відрізнятися між собою, як завгодно мало

Але похідні від них для деяких значень х і великих значень n можуть значно відрізнятися між собою:

, .

З наведеного прикладу та інших міркувань випливає, що із зростанням порядку похідної точність чисельного диференціювання здебільшого різко спадає. Тому на практиці формули чисельного диференціювання для похідних, вище від другого, застосовуються досить рідко.

1⁰. Формули чисельного диференціювання, побудовані за інтерполяційною формулою Ньютона. Нехай функцію 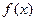задано у вузлах значеннями функції . Тоді інтерполяційний поліном Ньютона має вигляд

(3)

Нехай значення функції задано в рівновіддалених вузлах , де . З’ясуємо зв’язок між скінченими і розділеними різницями у випадку рівновіддалених вузлів, тобто коли . Покажемо, що справедлива формула

Доведення здійснимо методом математичної індукції. Для розділених різниць першого порядку

для розділених різниць другого порядку

тобто при формула справедлива. Припустимо, що вона справедлива при . Доведемо, що вона справедлива при . Справді,

що і треба було довести.

При маємо

Таким чином, інтерполяційний поліном Ньютона можна записати у вигляді

(4)

В обчислювальній практиці зручніше користуватись іншою формулою запису многочлена Ньютона (4). Якщо покласти

, то , , …, ,

і многочлен (4) матиме вигляд

(5)

Врахувавши, що

, ,

дістанемо:

(6)

. (7)

Поклавши в формулах (6), (7) , дістанемо:

(8)

. (9)

Із (8), якщо взяти перший доданок, якщо взяти перші два доданки, одержуємо:

, .

Із (9), якщо взяти перший доданок, одержуємо:

Приклад 1. У точках і знайти першу і другу похідні для функції , користуючись формулою Ньютона.

Розв’язання. Користуючись програмою Mathcad побудуємо таблицю різниць. Результати обчислень наведено на лістингу 1. Тут спочатку обчислюємо значення функції у вузлах. Потім будуємо таблицю(матрицю) різниць і записуємо формулу для наближеного обчислення похідної у загальному випадку і для точки . Одержані результати порівнюються з точними значеннями похідної.