Основи теорії випадкової похибки

У основі теорії випадкових похибок лежать два припущення:

а) при великій кількості вимірів похибки однакової величини, але різного знаку зустрічаються однаково часто;

б) імовірність появи похибки зменшується зі зростанням її величини (тобто, малі похибки зустрічаються частіше, великі – рідше).

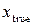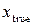Відповідно до цієї теорії, випадкові похибки підлягають закону нормального розподілу випадкових величин – закону Гаусса. Зміст його полягає в наступному. Припустимо, необхідно виміряти деяку фізичну величину, істинне значення якої нам невідоме. Через випадкові похибки ми, виконавши окремих вимірювань, замість одержуємо набір значень . Виявляється, що за допомогою закону розподілу ми, хоча і не можемо вказати точне значення 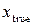, але можемо знайти, з якою ймовірністю величина 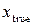опиниться всередині заданого числового інтервалу значень . Цей числовий інтервал значень називається довірчим інтервалом,а ймовірність того, що результат вимірів потрапляє в заданій довірчий інтервал, називається надійною ймовірністю(абонадійністю).Рівень значущості дорівнює ймовірності того, що величина 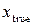не потрапляє у вказаний числовий інтервал.

За законом Гаусса, функція густини розподілу випадкових помилок має вигляд (рис. 1.1):

, (3)

а надійна імовірність потрапляння випадкової величини в інтервал визначається так:

. (4)
Рис. 1.1. Функція розподілу Гаусса.

 

Тут 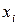– набір значень, отриманих при вимірах, – їх середнє арифметичне (математичне очікування), яке вважається найкращою оцінкою істинного значення результату вимірів. За міру розсіювання (розкиду) значень випадкової величини править дисперсія вибірки

, (5)

що характеризує швидкість зменшення ймовірності появи похибки зі збільшенням величини цієї похибки. Для характеристики розсіювання результатів вимірів користуються поняттям стандартного відхиленняабо середньої квадратичної (стандартної) похибки окремого виміру , яка дорівнює кореню квадратному з дисперсії вибірки. Величина характеризує середню похибку результату окремого виміру (тобто похибку самого методу вимірів), і обчислюється за формулою:

. (6)

Величина є мірою вірогідності результату виміру і входить до функції розподілу Гаусса. Гауссова крива має симетричний дзвіноподібний вигляд і характеризується двома параметрами: положенням вершини та “шириною” – відстанню між точками перегину (у яких друга похідна обертається на нуль). Середнє арифметичне результатів окремих вимірів являє собою середину довірчого інтервалу, а характеризує вплив випадкових похибок на результат: чим менше , тим вужче крива розподілу похибок окремих вимірів, тим точніше проведений вимір. Однак, з іншого боку, чим більш широким вибирається довірчий інтервал, тим вище ймовірність потрапляння випадкового значення у цей інтервал.

Для генеральної сукупності результатів вимірів, коли , середнє арифметичне дорівнює істинному значенню вимірюваної величини, якщо, звичайно, результати вимірів не містять систематичної похибки.

Підставивши із (3) в (4), можна розрахувати надійну ймовірність для будь-якого довірчого інтервалу . Наприклад, при великій кількості вимірів ( ), вибравши , одержимо величину надійності (див. рис. 1.1). Це означає, що 68,3% усіх результатів вимірів належать до інтервалу . Аналогічно можна показати, що для інтервалу надійна ймовірність , а для відповідно . Останнє означає, що за межами довірчого інтервалу півшириною опиняється лише 0,3% результатів усіх вимірів.

Звідси випливає так зване “правило ”:помилку, що виходить за межі числового інтервалу , вважають промахом(тому що ймовірність її появи всього 0,3%) і виключають результат відповідного виміру з подальшого розгляду. Проте слід нагадати, що - це генеральне середньоквадратичне відхилення (для дуже великої кількості вимірів ), а отже у звичайних вимірах (для невеликої вибірки, ) воно залишається невідомим. Тому при малих вибірках “правило ”застосовувати не слід. В інженерній практиці зазвичай вважають достатньою надійність ,хоча в деяких випадках (для вимірів, за умовами яких потрібен надзвичайно високий ступінь надійності, наприклад, коли йдеться про життя людей) іноді задають значення надійної імовірності , тобто ступінь ризику (рівень значущості ) становить лише 0,1%.

Для обмеженої вибірки середнє значення дещо відрізняється від 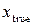. Сукупність середніх для деякої кількості вибірок (по окремих вимірів у кожній вибірці) теж описується функцією розподілу Гаусса

. (7)

де - середнє значення окремої вибірки, - середня квадратична (стандартна) похибка середнього.

Основний сенс усереднення результатів багаторазових вимірів полягає в тому, що середнє значення фізичної величини має меншу випадкову похибку, ніж результати окремих вимірів. Операція усереднення не усуває цілком випадковий характер середнього результату, а лише зменшує ширину інтервалу його невизначеності. Як вказувалося вище, величина характеризує точність даного способу вимірів (міру розсіювання результатів окремих вимірів). Однак, середнє значення фізичної величини є узагальненням результатів усіх вимірів, тому є всі підстави вважати, що воно є більш надійним, ніж результат кожного окремого виміру. Похибка середнього значення шуканої фізичної величини - середня квадратична (стандартна) похибка середнього обчислюється за формулою:

. (8)

Якщо в науковій роботі наводиться значення похибки і не вказується надійна ймовірність , то мається на увазі стандартна похибка середнього.

Отже, для характеристики величини випадкової похибки необхідно задати два числа: величину самої похибки (півширину довірчого інтервалу ) та величину надійної ймовірності .

Наведені вище значення надійних ймовірностей для інтервалів , , справедливі лише для генеральної сукупності вимірів –їхньої нескінченної безлічі. На практиці ж завжди здійснюється обмежена кількість вимірів – мала вибірка. Як же змінюється вірогідність результату в залежності від кількості вимірів?

Англійський математик В.С. Госсет, який публікував свої роботи під псевдонімом Стьюдент, у 1908 році вивів розподіл похибок середніх значень при малій кількості вимірів. Для великих вибірок ( ) цей розподіл практично збігається з розподілом Гаусса. Розподіл Стьюдента дозволяє за надійною ймовірністю та кількістю вимірів визначати відповідний довірчий інтервал. Для цього користуються спеціальною таблицею коефіцієнтів Стьюдента , що залежать від та (табл. 1.1). Коефіцієнти Стьюдента показують, у скільки разів потрібно збільшити стандартний довірчий інтервал, щоб при заданій кількості вимірів одержати необхідну надійність результату . За стандартний приймається довірчий інтервал .

Якщо результати окремих вимірів 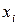підлягають нормальному розподілу Гаусса і є однаково точними – тобто виконані на одній апаратурі, з однаковою старанністю і тим самим методом – то випадкова похибка шуканої величини визначають за формулою:

. (9)

 

Таблиця 1.1

Коефіцієнти Стьюдента

1,84 6,31 12,71 31,82 63,66 212,21
1,32 2,92 4,30 6,96 9,92 18,22
1,20 2,35 3,18 4,54 5,84 8,89
1,14 2,13 2,78 3,75 4,60 6,43
1,11 2,02 2,57 3,36 4,03 5,38
1,09 1,94 2,45 3,14 3,71 4,80
1,08 1,89 2,36 3,00 3,50 4,44
1,07 1,86 2,31 2,90 3,36 4,20
1,06 1,83 2,26 2,82 3,25 4,02
1,05 1,81 2,23 2,76 3,17 3,89
1,05 1,80 2,20 2,72 3,11 3,79
1,04 1,78 2,18 2,68 3,05 3,71
1,04 1,77 2,16 2,65 3,01 3,64
1,04 1,76 2,14 2,62 2,98 3,58
1,04 1,75 2,13 2,60 2,95 3,54
1,03 1,75 2,12 2,58 2,92 3,49
1,03 1,74 2,11 2,57 2,90 3,46
1,03 1,73 2,10 2,55 2,88 3,43
1,03 1,73 2,09 2,54 2,86 3,40
1,03 1,72 2,09 2,53 2,85 3,38
1,03 1,72 2,08 2,52 2,83 3,35
1,02 1,72 2,07 2,51 2,82 3,34
1,02 1,71 2,07 2,50 2,81 3,32
1,02 1,71 2,06 2,49 2,80 3,30
1,02 1,71 2,06 2,49 2,79 3,29
1,02 1,71 2,06 2,48 2,78 3,27
1,02 1,70 2,05 2,47 2,77 3,26
1,02 1,70 2,05 2,47 2,76 3,25
1,02 1,70 2,05 2,46 2,76 3,24
1,01 1,68 2,02 2,43 2,71 3,17
1,01 1,68 2,01 2,40 2,68 3,12
1,01 1,67 2,00 2,39 2,66 3,10
1,00 1,64 1,96 2,33 2,58 2,97

При зі зростанням числа вимірювань коефіцієнти Стьюдента зменшуються мало. Тому виконувати вимірювання більше 30 разів недоцільно - це не призведе до скільки-небудь помітного зменшення випадкової похибки результату серії вимірювань.