Аксиомы группы
Теорема 1. Если в полугруппе существует левый нейтральный элемент е такой, что  при любом
при любом 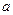 , и для любого элемента
, и для любого элемента 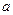 существует левый обратный элемент
существует левый обратный элемент  , т. е. такой, что
, т. е. такой, что  , то полугруппа является группой.
, то полугруппа является группой.
Доказательство. Докажем, что левый нейтральный элемент является и правым нейтральным, т. е.  при любом
при любом 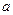 . Пусть
. Пусть  ,
,  - левые обратные элементы для
- левые обратные элементы для 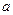 и
и  соответственно. Тогда
соответственно. Тогда  и
и  . Таким образом,
. Таким образом,  при любом
при любом 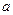 . Теперь докажем, что левый обратный элемент
. Теперь докажем, что левый обратный элемент  элемента
элемента 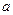 является и правым обратным, т. е.
является и правым обратным, т. е.  . С одной стороны,
. С одной стороны,  , но
, но  , т.е.
, т.е.  . Следовательно,
. Следовательно,  является правым обратным элементом. Теорема доказана.
является правым обратным элементом. Теорема доказана.
В дальнейшем в мультипликативной записи вместо  будем использовать
будем использовать  .
.
Теорема 2. Если в полугруппе имеется левый нейтральный элемент и правый нейтральный элемент, то они совпадают.
Доказательство. Пусть 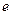 и
и  левый и правый нейтральные элементы. Тогда
левый и правый нейтральные элементы. Тогда  (
( 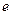 - левый нейтральный элемент) и
- левый нейтральный элемент) и  (
(  - правый нейтральный элемент), т. е.
- правый нейтральный элемент), т. е.  . Теорема доказана.
. Теорема доказана.
Из этой теоремы следует, что полугруппа содержит только один левый нейтральный элемент, т.к. любой левый нейтральный элемент равен выбранному правому нейтральному элементу  . Аналогично утверждение, что подгруппа содержит единственный правый нейтральный элемент. Поэтому в группе существует только один нейтральный элемент. При использовании мультипликативной записи нейтральный элемент группы называется единицей и обозначается 1.
. Аналогично утверждение, что подгруппа содержит единственный правый нейтральный элемент. Поэтому в группе существует только один нейтральный элемент. При использовании мультипликативной записи нейтральный элемент группы называется единицей и обозначается 1.
Теорема 3. В группе уравнений  при заданных
при заданных 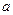 и
и  имеет единственное решение
имеет единственное решение  . Уравнение
. Уравнение  имеет единственное решение
имеет единственное решение  .
.
Доказательство. Положим  . Тогда
. Тогда  . Мы показали, что решение уравнения
. Мы показали, что решение уравнения  существует. Докажем единственность. Пусть
существует. Докажем единственность. Пусть  - произвольное решение уравнения
- произвольное решение уравнения  . Тогда
. Тогда  и
и  ,
,  ,
,  , Таким образом, произвольное решение совпадает с найденным ранее, т.е. единственность доказана. Уравнение
, Таким образом, произвольное решение совпадает с найденным ранее, т.е. единственность доказана. Уравнение  рассматривается аналогично. Теорема доказана.
рассматривается аналогично. Теорема доказана.
Из этой теоремы непосредственно следует единственность обратного элемента для любого элемента группы.
Определение. Группа (полугруппа) называется конечной, если она состоит из конечного числа элементов. Число элементов группы (полугруппы) называется ее порядком.
Невырожденные квадратные матрицы с вещественными элементами образуют группу относительно умножения. Эта группа не является абелевой и является бесконечной. Множество всех подстановок п элементов образует неабелеву группу относительно умножения порядка  . Эта группа называется симметрической группой.
. Эта группа называется симметрической группой.
Пусть  - группа, а
- группа, а  и
и  - два подмножества ее элементов.
- два подмножества ее элементов.
Определение. Произведением  подмножеств
подмножеств  и
и  группы
группы  называется множество произведений
называется множество произведений  , где
, где  ,
,  .
.
Произведение подмножеств группы ассоциативно, т. е.  , так как оба эти произведения составлены из элементов группы. Если одно подмножество состоит из одного элемента, например,
, так как оба эти произведения составлены из элементов группы. Если одно подмножество состоит из одного элемента, например,  , то произведение
, то произведение  обозначают
обозначают  , т. е. не отличают элемент от составленного из него одноэлементного множества.
, т. е. не отличают элемент от составленного из него одноэлементного множества.
Через  обозначим множество всех элементов, обратных к элементам множества
обозначим множество всех элементов, обратных к элементам множества  . Следует обратить внимание, Что множество
. Следует обратить внимание, Что множество  не является обратным к множеству
не является обратным к множеству  в смысле умножения подмножеств группы.
в смысле умножения подмножеств группы.