Біноміальний закон розподілу.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ХАРКІВСЬКА НАЦІОНАЛЬНА АКАДЕМІЯ
МІСЬКОГО ГОСПОДАРСТВА
МЕТОДИЧНІ ВКАЗІВКИ
До виконання контрольної роботи з курсу
ТЕОРІЯ ЙМОВІРНОСТЕЙ І
МАТЕМАТИЧНА СТАТИСТИКА»
Для студентів 2 і 3 курсів ФПО і ЗН спеціальностей
7.050107 "Економіка підприємства"
7.050106 "Облік і аудит")
Харків – ХНАМГ – 2007
Методичні вказівки до виконання контрольної роботи з курсу «Теорія ймовірностей і математична статистика» (для студентів 2 і 3 курсів ФПО і ЗН спеціальностей 7.050107 "Економіка підприємства", 7.050106 "Облік і аудит"). Укл.: Воронкова Т.Б., Воронков О.О.- Харків: ХНАМГ, 2007.- 32 с.
Укладачі: Т.Б. Воронкова, О.О. Воронков
Рекомендовано кафедрою Економіки й управління в будівництві і міському господарстві, протокол № 1 від 30.08.06 р.
 |
ЗАГАЛЬНІ ВІДОМОСТІ
Вивчення дисципліни «Теорія ймовірностей і математична статистика» передбачено програмою підготовки бакалавра за напрямком «Економіка й підприємництво». Теорією ймовірностей називають розділ математики, що вивчає закономірності у випадкових явищах. Методи теорії ймовірностей широко використовують в різних практичних задачах техніки, економіки, планування виробництва й інших. Теорія ймовірностей є теоретичною основою математичної статистики. У результаті вивчення курсу студент повинен володіти основними методами статистичного опису результатів спостереження, визначення імовірнісних характеристик випадкових величин, перевірки статистичних гіпотез і прийняття на їхній основі обґрунтованих рішень.
У процесі вивчення предмета «Теорія ймовірностей і математична статистика» студент повинен виконати контрольну роботу, що включає 7 завдань, які належать до різних тем курсу. У методичних вказівках приведено основні формули й теоретичні положення, а також розглянуто приклади розв'язання задач.
Номер варіанта контрольного завдання вибирають за двома останніми цифрами номера залікової книжки. Усього варіантів - 15. Якщо дві останні цифри залікової книжки перевищують число 15, то номер варіанта визначають шляхом вирахування числа, кратного 15, від 15 до 90. Наприклад, номеру залікової книжки, що закінчується цифрами 86, відповідає варіант 11. Контрольну роботу треба виконати в терміни, передбачені навчальним графіком. У процесі виконання завдання варто приводити відповідні пояснення. Наприкінці роботи слід привести список літератури, яку студент використовував при виконанні контрольної роботи.
На титульному аркуші необхідно чітко написати назву дисципліни, варіант завдання, прізвище, ім'я та по батькові, вказати курс, спеціальність і факультет.
ПРОГРАМА КУРСУ
Тема 1. ЙМОВІРНІСТЬ ВИПАДКОВОЇ ПОДІЇ. Основні поняття теорії ймовірностей. Класичний і статистичний методи визначення імовірності випадкової події. Закон великих чисел. Операції над подіями. Теореми теорії ймовірностей. Формула повної ймовірності. Формула Бейеса. Повторні незалежні випробування, формула Бернуллі. Локальна й інтегральна теореми Лапласа. Формула Пуассона.
Тема 2. ВИПАДКОВА ВЕЛИЧИНА І ЇЇ ЗАКОНИ РОЗПОДІЛУ Поняття випадкової величини. Закон розподілу випадкової величини. Функція розподілу й щільність розподілу ймовірностей і їхні властивості. Числові характеристики випадкової величини. Моменти випадкової величини: початкові й центральні. Теореми про числові характеристики.
Тема 3. СИСТЕМА ВИПАДКОВИХ ВЕЛИЧИН. ЗАКОНИ РОЗПОДІЛУ Й ЧИСЛОВІ ХАРАКТЕРИСТИКИ СИСТЕМИ. Поняття системи випадкових величин. Система двох випадкових величин. Функція розподілу й щільність розподілу ймовірностей системи двох випадкових величин. Числові характеристики системи, кореляційний момент і коефіцієнт кореляції. Функції випадкових величин.
Тема 4. ОСНОВНІ ЗАКОНИ РОЗПОДІЛУ ВИПАДКОВИХ ВЕЛИЧИН.Біноміальний закон розподілу. Закон розподілу Пуассона. Експонентний закон розподілу. Нормальний закон розподілу. Центральна гранична теорема. Логарифмічно нормальний розподіл. Закон рівномірної щільності.
Тема 5. ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ СТАТИСТИКИ. Поняття генеральної й вибіркової сукупностей. Визначення закону розподілу випадкової величини за статистичним даними. Вирівнювання статистичних рядів. Оцінки числових характеристик випадкових величин і їхні властивості. Довірчий інтервал і довірча ймовірність. Статистичні гіпотези. Нульова й альтернативна гіпотези. Область прийняття гіпотези. Критерії згоди.
Тема 6. ЕЛЕМЕНТИ РЕГРЕСІЙНОГО АНАЛІЗУ. Функція регресії. Згладжування експериментальних залежностей за методом найменших квадратів. Перевірка адекватності рівняння регресії за критерієм Фішера. Оцінка значимості коефіцієнтів рівняння регресії.
Тема 7. ЕЛЕМЕНТИ КОРЕЛЯЦІЙНОГО АНАЛІЗУ. Кореляційна залежність. Визначення тісноти зв'язку в кореляційній залежності.Коефіцієнт регресії.
Тема 8. ЕЛЕМЕНТИ ДИСПЕРСІЙНОГО АНАЛІЗУ. Однофакторний дисперсійний аналіз. Мінливість середніх. Критерій z.
Тема 9. ЕЛЕМЕНТИ ТЕОРІЇ ВИПАДКОВИХ ПРОЦЕСІВ. Визначення випадкового процесу, імовірнісні характеристики. Стаціонарний випадковий процес. Ергодична гіпотеза. Кореляційна функція.
ОСНОВНІ ПОЛОЖЕННЯ
Завдання 1 варто виконувати після вивчення теми «Ймовірність випадкової події». Для розв'язання задач варто використовувати класичний метод визначення ймовірності випадкової події
Р(А)= m/n , (1)
де n – загальне число можливих наслідків досліду; m – число наслідків досліду, які сприятливі появі події А;
а також теореми додавання й множення.
Р(А + В) = Р(А) + Р(В) - Р(А*В) (2)
Р(А + В) = Р(А) + Р(В) (3)
P(A) = 1 - P((A).
Р(А * В) = Р(А) * Р(В|А); (4)
формулу повної ймовірності:
Р(А)= Р(H1)*Р(А|H1)+Р(H2)*Р(А|H2)+ … +Р(HN)*Р(А|HN); (5)
формулу Бейеса
Р(Нi|А)= Р(Нi)*Р(А|Нi) /SР(Нi)*Р(А|Нi) (6)
формулу Бернуллі
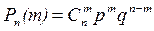 (7)
(7)
де 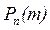 - ймовірність того, що в n випробуваннях подія А з'явиться рівно m разів;
- ймовірність того, що в n випробуваннях подія А з'явиться рівно m разів;
 - число сполучень з n елементів до m;
- число сполучень з n елементів до m;
р – імовірність появи події А в одному досліді;
q = 1 – p – імовірність не появи події А в одному досліді.
Приклад 1. Три спортсмени стріляють по мішені по одному разу. Імовірність влучення для першого з них дорівнює 0,8; для другого - 0,85; для третього - 0,9. Визначити ймовірність того, що:
1) всі спортсмени влучать в мішень;
2) жоден не влучить;
3) тільки один спортсмен влучить в мішень;
4) тільки два спортсмени влучать в мішень;
5) хоча б один спортсмен влучить в мішень.
Рішення. Позначимо події А1, А2, А3 — перший, другий, третій спортсмени відповідно влучать в мішень. Тоді
Р(А1)=0,8; Р(`А1)=0,2;
Р(А2)=0,85; Р(`А2)=0,15;
Р( А3)=0,9; Р(`А3)=0,1.
1) Ймовірність того, що всі спортсмени влучать в мішень, знаходимо за теоремою множення ймовірностей для незалежних подій.
Р(А1*А2*А3)= 0,8 * 0,85 * 0,9 =0,612.
2) Ймовірність того, що жоден із спортсменів не влучить в мішень, знаходимо за теоремою множення для незалежних подій
Р(`А1*`А2*`А3)= 0,2 * 0,15 * 0,1 =0,003.
3) Для обчислення ймовірності того, що тільки один спортсмен влучить в мішень, використаємо теореми додавання для неспільних подій і множення для незалежних подій:
р=Р( А1)*Р(`А2)*Р(`А3)+Р(`А1)*Р( А2)*Р(`А3)+Р(`А1)*Р(`А2)*Р( А3) =
=0,8*0,15*0,1+0,2*0,85*0,1+0,2*0,15*0,9= 0,056.
4) Для обчислення ймовірності того, що тільки два спортсмени потраплять в мішень, також використаємо теореми додавання для неспільних подій і множення для незалежних подій:
р=Р( А1)*Р(А2)*Р(`А3)+Р(`А1)*Р( А2)*Р(А3)+Р(А1)*Р(`А2)*Р(А3) =
= 0,8*0,85*0,1+0,2*0,85*0,9+ 0,8*0,15*0,9= 0,329.
5) Подія “хоча б один із спортсменів влучить в мішень” протилежна події ”жоден із спортсменів не влучить в мішень”. Таким чином, маємо
р= 1 - Р(`А1*`А2*`А3)= 1 - 0,003 =0,997.
Приклад 2. У складальний цех надходять однакові деталі, які виробляють у двох інших цехах заводу. Перший цех доставляє 70%, а другий - 30% деталей. При цьому перший цех виробляє 95% деталей вищої якості, а другий - 90%. Навмання обрана деталь виявилася вищої якості. Знайти ймовірність того, що ця деталь: 1) з першого цеху; 2) із другого цеху.
Рішення. Позначимо подію А - деталь вищої якості. Висуваємо гіпотези: гіпотеза Н1 - деталь із першого цеху; гіпотеза Н2 - деталь із другого цеху. Тоді, апріорні ймовірності гіпотез: Р(Н1) = 0,7, Р(Н2) = 0,3. Умовні ймовірності події А при кожній з гіпотез відповідно дорівнюють: Р(А/Н1) = 0,95, Р(А/Н2) = 0,9. За формулою Бейеса маємо:
імовірність того, що деталь із першого цеху -
Р(Н1/А)= Р(Н1)*Р(А/Н1) / [Р(Н1)*Р(А/Н1)+Р(Н2)*Р(А/Н2)] =
= 0,7*0,95/(0,7*0,95+0,3*0,9) = 0,71;
імовірність того, що деталь із другого цеху -
Р(Н2/А)= Р(Н2)*Р(А/Н2) / [Р(Н1)*Р(А/Н1)+Р(Н2)*Р(А/Н2)] =
= 0,3*0,9/(0,7*0,95+0,3*0,9) = 0,29.
Завдання 2 і 3 варто виконувати після вивчення теми «Випадкова величина і її закони розподілу». Нагадаємо основні положення.
Випадковою називають величину, що в результаті досліду може прийняти те або інше значення. Розрізняють дискретні й безперервні випадкові величини.
Законом розподілу випадкової величини називають будь-яке правило, що дозволяє знаходити ймовірності різних значень випадкової величини.
Ряд розподілу - таблиця, у верхньому рядку якої перераховано всі значення випадкової величини х1, х2, …, хn у порядку їхнього зростання, а в нижньому - імовірності появи цих значень р1, р2, …, рn:
| хi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
Функція розподілу випадкової величини Х це ймовірність того, що випадкова величина прийме значення, менше x:
F(х) = P{X £ x} (8)
Властивості:
1. Значення функції розподілу належать відрізкові [0; 1].
2. Функція розподілу - неубутна функція, тобто
F(x2) ³ F(x1), якщо x2 > x1 .
3. Імовірність того, що випадкова величина Х прийме значення, укладене в інтервалі (a, b), дорівнює приростові функції розподілу на цьому інтервалі:
P{a ≤ X ≤ }= F(b) - F(a).
4. Якщо всі можливі значення випадкової величини X належать інтервалові(- ¥, + ¥), то примінус нескінченності функція розподілу дорівнює нулю, а при плюс нескінченності — одиниці, тобто F(- ¥) = 0;F(+ ¥) = 1.
Щільність розподілу – це похідна від F(х) по х :
f(x) = d(х) / dx. (9)
Властивості:
1. Щільність розподілу невід’ємна, тобто f(x) ³ 0 як похідна неубутної функції.
2. Інтеграл від щільності розподілу в нескінченних межах дорівнює одиниці:
 . (10)
. (10)
3. Ймовірність влучення безперервної випадкової величини в інтервал (a, b)
 . (11)
. (11)
4. Функцію розподілу визначають співвідношенням:
 (12)
(12)
Числові характеристики випадкової величини:
математичне сподівання Х
 (13)
(13)
 (14)
(14)
другий початковий момент a2:
 (15)
(15)
 (16)
(16)
дисперсія
 (17)
(17)
 , (18)
, (18)
де  ;
;
Dx = a2 – mx2.
середнє квадратичне відхилення
sх = ÖDx. (19)
Приклад 3. Задано ряд розподілу
| хі | 1,4 | 1,8 | 2,3 | 3,2 |
| рі | 0,3 | 0,4 | 0,2 | 0,1 |
Знайти математичне сподівання М[Х], дисперсію D[Х] і середнє квадратичне відхилення s[Х].
Рішення. Математичне сподівання випадкової величини Х
М[Х]=х1*р1+х2*р2+х3*р3+х4*р4=
= 1,4 * 0,3 + 1,8*0,4 + 2,3 * 0,2 + 3,2 * 0,1 = 1,92.
Дисперсія
D[Х] = (х1 - М[Х])2 * р1 + (х2 - М[Х])2 * р2 + (х3 - М[Х])2 р3 + (х4* - М[Х])2р4 =
= (1,4-1,92) 2 * 0,3 + (1,8 -1,92) 2 * 0,4 + (2,3-1,92) 2 * 0,2 + (3,2-1,92) 2 * 0,1 = 0,28.
або М[Х2]= 1,42 * 0,3 + 1,82 * 0,4 + 2,32 * 0,2 + 3,22 * 0,1 = 3,966;
D[Х] = М[Х2] – (М[Х])2 = 3,966 – 1,922 = 0,28.
Середнє квадратичне відхилення випадкової величини Х:
s[Х]=ÖD[Х] = Ö0,28 = 0,53.
Приклад 4. Випадкову величину X задано функцією розподілу:

Знайти щільність розподілу ймовірностей, визначити математичне сподівання, дисперсію, побудувати графіки функцій f(х) і F(х)
Рішення
а) Знайдемо щільність ймовірностей:

б) Визначимо математичне сподівання X:

Знайдемо дисперсію Х:
 .
.
в) Побудуємо графіки функцій f(х) і F(х).
 |
Завдання 4 варто виконувати після вивчення теми «Основні закони розподілу випадкових величин».
Біноміальний закон розподілу.
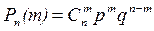 (20)
(20)
де 0 < р < 1; q = 1 – p.
Закон розподілу Пуассона.
 (21)
(21)