Приклад виконання завдання. 2.1. Предмет кінематики. Простір і час в класичній механіці
КІНЕМАТИКА
Розділ ІІ
Вступ до кінематики
2.1. Предмет кінематики. Простір і час в класичній механіці. Відносність механічного руху. Система відліку. Задачі кінематики.
Кінематика точки
2.2. Векторний спосіб задання руху точки. Траєкторія руху точки. Вектори швидкості і прискорення точки.
2.3. Координатний спосіб задання руху точки в декартових координатах. Визначення швидкості і прискорення точки по їх проекціям на координатні осі. Натуральний спосіб задання руху точки. Швидкість та прискорення точки в проекціях на осі натурального тригранника. Дотичне і нормальне прискорення точки.
Кінематика твердого тіла
2.4. Поступальний рух твердого тіла. Теорема про траєкторії, швидкості та прискорення точок твердого тіла.
2.5. Обертання твердого тіла навколо нерухомої вісі. Рівняння обертального руху тіла. Кутова швидкість і кутове прискорення тіла.
Швидкість і прискорення точки твердого тіла, котре обертається навколо нерухомої вісі. Вектори кутової швидкості і кутового прискорення тіла.
2.6. Плоскопаралельний або плоский рух твердого тіла і рух плоскої фігури в її площині. Рівняння руху плоскої фігури. Розкладання руху плоскої фігури на поступальний разом з полюсом та обертальний навколо полюса. Незалежність кутової швидкості і кутового прискорення фігури від вибору полюса. Визначення швидкості любої точки фігури. Теорема про проекції швидкості двох точок фігури. Миттєвий центр швидкостей; визначення з його допомогою швидкостей точок плоскої фігури. Визначення прискорення любої точки плоскої фігури.
2.7.* Рух твердого тіла навколо нерухомої точки або сферичний рух. Кути Ейлера. Рівняння руху твердого тіла навколо нерухомої точки. Миттєва вісь обертання. Вектори кутової швидкості і кутового прискорення тіла.
Визначення швидкостей та прискорень точок тіла.
2.8.* Загальний випадок руху вільного твердого тіла. Рівняння руху вільного твердого тіла. Розкладання цього руху на поступальний разом з полюсом і рух навколо полюса. Визначення швидкостей і прискорень точок тіла.
Складний рух точки і твердого тіла
2.9. Абсолютний та відносний рух точки; переносний рух. Теорема про додавання швидкостей.
Теорема Коріоліса про додавання прискорень; визначення коріолісового прискорення. Випадок поступального переносного руху.
2.10.* Складний рух твердого тіла. Додавання поступальних рухів. Додавання миттєвих обертань тіла навколо осей, які перетинаються, та навколо паралельних осей.
Пара миттєвих обертань. Кінематичний гвинт. Миттєва гвинтова вісь.
КІНЕМАТИКА
Кінематика точки
Рух точки по відношенню до вибраної системи відліку вважається заданим, якщо відомий спосіб, за допомогою якого можна визначити положення точки в любий момент часу.
Векторний спосіб
Для того, щоб визначити закон руху точки векторним способом, необхідно визначити радіус-вектор цієї точки як функцію часу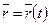 
.
Швидкість точки при векторному способі визначення руху знаходиться як перша похідна за часом від її радіус-вектора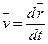 
,
а прискорення – як друга похідна за часом від її радіус-вектора або як перша похідна за часом від її вектора швидкості
.
Координатний спосіб
Положення точки по відношенню до будь-якої системи координат повністю визначається координатами точки. Якщо координати точки задати в вигляді відомих функцій часу, то положення точки можна визначити в любий момент часу. Такий спосіб задання руху точки називається координатним і він вимагає вибору конкретної системи координат (декартової, сферичної, циліндричної).
Для того, щоб визначити закон руху точки в декартовій системі координат, необхідно визначити координати цієї точки як функції часу
Проекції векторів швидкості та прискорення на осі декартових координат визначаються за формулами:
Модуль швидкості та прискорення в цьому випадку визначаються за формулами
.
Лінія, яку описує точка в певній системі відліку, називається траєкторією даної точки у цій системі відліку.
Для того, щоб знайти рівняння траєкторії точки в декартовій системі координат, необхідно з рівнянь руху виключити параметр t (час).
Натуральний спосіб
Для того, щоб визначити закон руху точки натуральним способом, необхідно вказати:
а) траєкторію точки;
б) початок відліку дугової координати точки на цій траєкторії;
в) напрямок додатнього відліку дугової координати на траєкторії;
г) дугову координату точки як функцію часу 
Натуральні осі
Натуральними осями називають три взаємно перпендикулярні осі:
а) дотична: орт дотичної 
спрямований в сторону додатнього відліку дугової координати;
б) головна нормаль: орт головної нормалі 
спрямований до центра кривизни траєкторії;
в) бінормаль: орт бінормалі 
спрямований так, щоб три взаємно перпендикулярні осі 
створювали праву систему координат (як 
).
Проекції вектора швидкості на натуральні осі координат визначаються за формулами
.
Модуль вектора швидкості
.
Проекції вектора прискорення на натуральні осі координат визначаються за формулами
де 
- поточний радіус кривизни траєкторії.
Модуль вектора прискорення
Дотичне прискорення точки характеризує зміну її швидкості за величиною.
Нормальне прискорення точки характеризує зміну її швидкості за напрямком.
Дотичне прискорення точки дорівнює нулю при русі цієї точки зі сталою, за величиною швидкістю, а також у ті моменти часу, коли величина швидкості досягає експериментальних значень.
Нормальне прискорення точки дорівнює нулю при прямолінійному русі точки, у точках перегину її траєкторії, а також у ті моменти часу, коли точка змінює напрямок свого руху на протилежний.
Якщо рух точки заданий в декартовій системі координат, то величини її дотичного та нормального прискорень визначають за формулами:
Характер руху точки у даний момент визначається так:
а) якщо кут між векторами швидкості і прискорення гострий, то рух – прискорений; якщо тупий, то – сповільнений;
б) якщо 
, то рух – прискорений, у протилежному випадку – сповільнений;
в) якщо 
, то рух прискорений, у протилежному випадку – сповільнений.
Приклад.
Рух точки задано рівняннями в декартовій системі координат
Знайти рівняння траєкторії, швидкість і прискорення точки, дотичне і нормальне прискорення рухомої точки, а також радіус кривизни. Побудувати траєкторію руху точки і показати на ній положення точки, її швидкість і прискорення для заданих моментів часу 
і 
.
Дано: 
см
см
Визначити 
Рішення.
1) Рівняння руху точки можна розглядати, як рівняння траєкторії, заданий в параметричному вигляді. Щоб отримати рівняння в декартовій системі координат з рівнянь руху необхідно виключити параметр t. Враховуючи, що 
, маємо 
так як 
, то 
, де 
Траєкторією руху точки є частина параболи розташованої на відрізку, що лежить в інтервалі 
Позначимо положення точки на траєкторії в задані моменти часу, коли
2) Визначимо швидкість точки за її проекціями на координатні осі
(см/с); 
(см/с)
(см/с)
Направляючі косінуси
В момент часу
см/с, 
Побудуємо вектор швидкості.
3) Визначимо прискорення за його проекціями на координатні осі
(см/с2); 
(см/с2)
Направляючі косинуси
В момент часу
(см/с2); 
(см/с2);
(см/с2)
коли
(см/с2)
(см/с2)
4) Обчислимо дотичне та нормальне прискорення
Дотичне прискорення
коли 
(см/с2);
.
Нормальне прискорення
після перетворення отримаємо
коли 
(см/с2)
В момент 
5) Визначення радіуса кривизни
Радіус кривизни визначається за формулою
(см)
коли , то 
і 
, радіус кривизни обчислити за кінематичними формулами немає змоги;
коли 
(см)
Визначені величини запишемо в вигляді таблиці
Час, 
| Координати точки | Швидкість, см/с | Прискорення, см/с2 | Радіус кривизни, см | |||||||
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| |
| –16 | –2 | 16,12 | 16,12 | – | |||||||
| –4 | –2 | –16 | 0,25 |
Кінематика твердого тіла
Поступальний рух
Поступальним рухом твердого тіла називається такий його рух, при якому пряма, що з’єднує дві довільні точки цього тіла, за весь час його руху переміщується паралельно самій собі.
Теорема
Всі точки твердого тіла, що рухається поступально, описують однакові траєкторії і в кожний момент часу мають геометрично рівні швидкості та прискорення.
Кінематичні рівняння поступально руху твердого тіла задаються рівняннями руху однієї з його точок у будь-якій формі. Швидкості та прискорення точки тіла при його поступальному русі визначаються за тими ж формулами, що й швидкість та прискорення точки за рівняннями її руху.
Обертальний рух
Рух твердого тіла називається обертальним деякій системі відліку, якщо у цьому тілі існують хоча б дві точки, які за весь час його руху залишаються нерухомими. Лінія, яка з’єднує ці нерухомі точки, називається віссю обертання.
Кінематичне рівняння руху тіла, яке обертається навколо нерухомої осі, визначається кутом його повороту як функцією часу 
.
Проекції векторів кутової швидкості та кутового прискорення тіла на вісь його обертання визначаються за формулами 
,
вісь 
- направлена по осі обертання.
Якщо 
, то тіло обертається прискорено, в протилежному випадку – сповільнено.
Вектором кутової швидкості обертання тіла називається вектор, направлений по осі обертання так, щоб з кінця цього вектора обертання тіла спостерігалось проти годинникової стрілки, за модулем рівний його кутовій швидкості.
Вектор кутового прискорення визначається як перша похідна за часом від вектора його кутової швидкості 
.
Модуль швидкості довільної точки тіла, яке обертається навколо нерухомої вісі, визначається за формулою
,
де 
- величина кутової швидкості тіла, 
- найкоротша відстань від точки до осі обертання тіла. Вектор швидкості точки тіла, лежить в площині перпендикулярній осі обертання, перпендикулярний до радіуса обертання навколо нерухомої осі та спрямований у сторону обертання тіла.
Модуль дотичного прискорення довільної точки тіла визначається за формулою 
,
- модуль кутового прискорення, і направлений в сторону швидкості, якщо рух прискорений, і в протилежну сторону швидкості, якщо рух сповільнений.
Модуль нормального прискорення визначається за формулою
,
де - кутова швидкість і направлена до осі обертання тіла.
Модуль прискорення довільної точки тіла, яке обертається навколо нерухомої осі, визначається за формулою
.
Вектор прискорення складає з радіусом обертання даної точки кут 
, котрий визначається за формулою
;
Приклад
1. Півколо радіуса 10 см почало обертатися навколо осі О1О2 без початкової кутової швидкості. В деякий момент дотичне прискорення точки А рівне  см/с2, а нормальне прискорення точки В -  см/с2. Визначити час, котрий пройшов від початку руху до цього моменту, і кут повороту півкола, якщо воно оберталось рівноприскорено.
Задано:  см/с2
 см/с2
R=10 см
 
| 
|
Рішення
Дотичне прискорення обчислюється за формулою 
, нормальне - 
. Для точки А - 
, для точки В - 
. Тоді 
, згідно за даними величинами маємо
.
Звідки 
рад/с2; 
; 
рад/с.
За умовою задачі , тоді кутова швидкість обчислюється за формулою 
, звідки 
(с).
Кут повороту знайдемо за формулою 
; так як 
, то 
; 
(рад).
Відповідь: 
=10 с; 
рад.
2. Диск парової турбіни при пуску обертається за законом 
рад.
Визначити в момент часу t=5 с швидкість та повне прискорення точки диска, що відстоїть від вісі обертання на 0,5 м.
Дано: 
м
Визначити: 
.
Рішення
Знаючи закон обертання турбіни , визначимо кутову швидкість та кутове прискорення турбіни
(рад/с)
(рад/с)
В момент часу 
с кутова швидкість дорівнює 
(рад/с);
кутове прискорення 
(рад/с2).
Швидкість точки, що відстоїть від осі обертання в цей момент часу 
(м/с);
повне прискорення
;
дотичне прискорення 
(м/с2);
нормальне прискорення 
(м/с2)=123,24 (м/с2)
повне прискорення
(м/с2)
=123,28 (м/с2).
Відповідь: 
(м/с); =123,28 (м/с2).
Приклад виконання завдання
|
Дано:  см;
 см;
 см;
 см;
 см;
  м=40см.
Визначити:  .
|
Рішення
Визначимо момент часу 
коли шлях S, пройдений вантажем, дорівнює 40 см
с.
Продиференціюємо за часом рівняння руху і отримаємо швидкість вантажу
(см/с).
Кутова швидкість другої ланки
(рад/с).
Визначимо кутову швидкість ланки 3, використовуючи співвідношення
(рад/с).
Кутове прискорення ланки 3
(рад/с2).
Швидкість точки М
(см/с)
і направлена по дотичній до кола 3 в сторону обертання.
Обертальне (дотичне) прискорення точки М
(см/с2).
і має однаковий напрямок зі швидкістю (рух коліс прискорений).
Доцентрове (нормальне) прискорення точки М
(см/с2)
і направлене по радіусу до центру колеса.
Повне прискорення точки М
.
Значення цих величин для моменту часу 
с зведемо в таблицю
| 
|  см/с
| Прискорення, см/с2 | ||
| 
|
| |||
| 11,87 | 13,33 | 474,8 | 533,2 | 5635,88 | 5661,05 |
