Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Сложение и вычитание алгебраических дробей с разными знаменателями (более сложные случаи)
1. Повторение сложения/вычитания обыкновенных дробей с разными знаменателями
На уроке мы продолжим тему предыдущего урока и будем рассматривать задачу сложения и вычитания алгебраических дробей с разными знаменателями, т.е. упрощение выражений вида: 
, где 
. В основном, задача сводится к нахождению наименьшего общего знаменателя дробей, а это делается, как мы уже знаем, по аналогии с обыкновенными дробями. Рассмотрим примеры.
Пример 1. Выполнить действие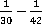 
.
Решение. Для нахождения наименьшего общего знаменателя дробей воспользуемся основной теоремой арифметики и разложим знаменатели на простые множители.
и 
. Следовательно, 
и 
.
Вспомним, что наименьший общий знаменатель должен содержать множители всех знаменателей, причем так, чтобы множителей было минимально возможное количество. В нашем случае необходимы множители 
. Следовательно, общий знаменатель 
, а дополнительные множители: к первой дроби 
, ко второй дроби 
.
.
Как видно из решения, удобно даже не перемножать простые множители в знаменателе до получения числителя общей дроби, чтобы потом было легче сокращать дробь.
Ответ. 
.
2. Примеры на сложение/вычитание двух алгебраических дробей с разными знаменателями с использованием разложения знаменателей на множители
Теперь рассмотрим аналогичные операции с алгебраическими дробями. Не сложно догадаться, что самой трудоемкой частью сложения или вычитания дробей с разными знаменателями является нахождение наименьшего общего знаменателя. Если в случае обыкновенных дробей можно было пользоваться разложением чисел на множители, то в алгебраических дробях на множители необходимо будет раскладывать многочлены. Для этого существует несколько известных нам методов: вынесение общего множителя, применение формул сокращенного умножения и метода группировки слагаемых. Рассмотрим более подробно их применение для решения сложных задач на сложение и вычитание алгебраических дробей с разными знаменателями.
Пример 2. Выполнить действия 
.
Решение. Для нахождения наименьшего общего знаменателя и дополнительных множителей разложим знаменатели на множители. Первый знаменатель уже представляет собой простое выражение, а второй раскладывается по формуле разности квадратов:
. Как видно по ходу решения, в качестве наименьшего общего знаменателя выбран знаменатель второй дроби, который делится и на первый знаменатель и сам на себя. Дополнительный множитель в таком случае пригодился только для первой дроби. Во втором переходе можно обратить внимание на внесение минуса перед дробью в один из множителей знаменателя для того, чтобы сделать знаменатели дробей максимально похожими друга на друга; такой прием нам уже знаком из темы «сложение алгебраических дробей с одинаковыми знаменателями (более сложные случаи)» (урок №5).
Ответ. 
.
Пример 3. Выполнить действия 
.
Решение. Поступим аналогично с предыдущим примером и разложим по ходу решения знаменатель второй дроби на множители по формуле разности квадратов, перед этим внесем минус перед дробью в знаменатель для того, чтобы он получил более удобный вид:
.
Ответ. 
.
3. Примеры на сложение/вычитание трех алгебраических дробей с разными знаменателями с использованием разложения знаменателей на множители
Рассмотрим теперь более сложные примеры на сложение/вычитание трех дробей.
Пример 4. Выполнить действия 
.
Решение. Как и ранее, разложим на множители каждый знаменатель, найдем наименьший общий знаменатель и дополнительные множители.
.
Как и ранее, для приведения выражения к удобному виду, вынесем минус из знаменателя второй дроби. Поскольку в выражении присутствует три дроби, чтобы не запутаться, выпишем наименьший общий знаменатель отдельно, составив его из множителей, входящих во все знаменатели: 
. Исходя из него, укажем и дополнительные множители для каждой из дробей, как те множители, которых не хватает знаменателю, чтобы стать общим.
.
Последний переход (раскрывание скобок) не принципиален, и можно было указать в ответ выражение, записанное предпоследним.
Ответ. 
.
Пример 5. Выполнить действия 
.
Решение. Поступаем уже известным для нас образом: раскрываем знаменатели на множители, при необходимости меняем знаки в знаменателях дробей, находим наименьший общий знаменатель и дополнительные множители.
.
Наименьший общий знаменатель: 
.
.
Можно заметить, что выражение в числителе 
представимо в виде 
по формуле квадрата суммы, аналогично выражение 
.
В конце проведено сокращение на 
, значит необходимо обязательно записать область недопустимых значений переменной, связанную с этим сокращением: 
и 
являются недопустимыми значениями переменных. Во всех остальных случаях выражение равно 
.
Ответ. .