Гармонический ряд (после чисел Ферма).
Ещё одно доказательство бесконечности множества простых чисел использует расходимость гармонического ряда. Эти слова означают, что сумма
1+1/2+1/3+ … +1/n
может быть сделана сколь угодно большой, надо только взять достаточно
много слагаемых.
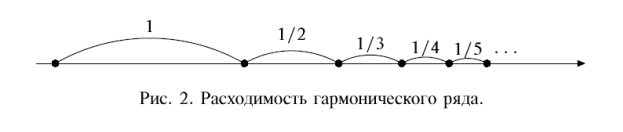
Наглядно это утверждение можно представлять себе так. Мы идём умень-
шающимися шажками - первый длины 1, второй 1/2, далее 1/3, 1/4,
1/5, . . . . Оказывается, что несмотря на уменьшение со временем
длины шага, таким манером можно уйти сколь угодно далеко.
Чтобы убедиться в этом, разделим гармонический ряд на части:

(в каждой скобке последнее слагаемое имеет в знаменателе степень двойки).
Правило тут такое: n-я по счёту скобка начинается с дроби 1/(2n + 1),
кончается дробью 1/2n+1 и содержит 2n слагаемых. (Скажем, следующая
скобка будет содержать числа от 1/9 до 1/16 включительно.) Наименьшее из
чисел в каждой из скобок - последнее, и если все слагаемые заменить на
него, то получится сумма
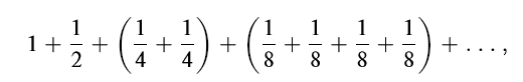
в которой каждая скобка равна 1/2. Поэтому если взять достаточно много
скобок, мы уйдём сколь угодно далеко, как и утверждалось.
Важно понимать, что сама по себе бесконечность числа слагаемых не
гарантирует, что мы далеко уйдём. Например, сколько ни бери слагаемых в
сумме

всё равно больше 2 не получится: каждый следующий член составляет половину оставшегося расстояния до точки 2, и мы на каждом шаге
приближаемся к этой точке вдвое, так никогда её и не достигнув. Формально
говоря,

чтобы убедиться в этом, достаточно перенести 1/2n из правой части в левую
и затем свернуть левую часть, объединяя одинаковые слагаемые.

Разница между этими двумя примерами объясняется тем, что в бесконечно убывающей прогрессии (втором примере) слагаемые убывают гораздо
быстрее.
Всё это замечательно, но при чём тут простые числа? Удивительным
образом связь существует, и очень глубокая. Давайте для начала перемножим
две суммы

(обратные степени двойки и тройки; сколько именно слагаемых в каждой
скобке, мы решим потом). После раскрытия скобок в произведении возникнут слагаемые 1 (как 1 · 1), 1/2 (как (1/2) · 1), 1/3 (как 1 · (1/3)), 1/4
(как (1/4) · 1), 1/6 (как (1/2) · (1/3)) и так далее. Заметьте, что при этом
пропущена 1/5, нет также 1/7, 1/10 и др. Формально говоря, произведение
двух скобок будет суммой всех дробей вида

при не слишком больших k и l (каких именно - зависит от того, сколько
членов мы взяли в наших двух суммах).
Чтобы восполнить хотя бы часть пропущенного, добавим третий множитель и рассмотрим произведение

Теперь уже есть знаменатели вида 2k 3l 5m (так что 1/5 и 1/10 вошли в
сумму), но, скажем, 1/7 по-прежнему нет. Чтобы появилась 1/7, надо домножить произведение на

и так далее.
Продолжая эти наблюдения, можно придти к такому выводу: если бы
простых чисел было конечное число n, то гармонический ряд бы не превысил
2n (а мы знаем, что это не так - значит, простых чисел бесконечно много).
В самом деле, пусть 2, 3, … , p - все простые числа и их всего n. В
этом случае произведение

содержит n сомножителей. Каждый из сомножителей меньше двух (про первый мы уже говорили, остальные почленно меньше первого). Значит, произведение меньше 2n . С другой стороны, взяв достаточно членов в каждой скобке, мы можем получить после раскрытия скобок сколь угодно длинный кусок гармонического ряда без пропусков (а дальше - с пропусками). Ведь мы предположили, что других простых чисел нет, значит, любой знаменатель представим в виде произведения имеющихся.
Таким образом, расходимость гармонического ряда неизбежно влечёт за
собой бесконечность множества простых чисел!
Замечание 1. Использовали ли мы в этом рассуждении однозначность
разложения чисел на простые множители? На самом деле нет. Если бы разложение на множители какого-либо числа N было неоднозначным, это привело бы к тому, что при раскрытии скобок у нас появилось несколько слагаемых вида 1/N (столько, сколько есть различных разложений). Но если даже с несколькими такими слагаемыми сумма не больше 2n , то уж с одним и подавно. А вот существование (хотя бы одного) разложения любого числа на простые множители мы действительно использовали, когда говорили, что в произведении можно получить любые члены гармонического ряда.
Замечание 2. Более тонкий анализ (основанный на тех же идеях) позволяет доказать, что не только гармонический ряд расходится, но и ряд

(в знаменателях - простые числа) тоже расходится.