Перетворення комплексного креслення
Передмова
Навчальна дисципліна Інженерна та комп’ютерна графіка - об’єднана. Вона складається з трьох розділів: „Нарисна геометрія”, „Технічне креслення” та „Комп’ютерна графіка”, які є органічним цілим, де одна частина розвиває і доповнює інші.
Проектування, виготовлення, експлуатація машин, механізмів, сучасних будинків і споруд, створення нових технологій пов’язані з різними видами зображень: рисунками, кресленнями, ескізами. Це насичує графічні навчальні дисципліни рядом важливих завдань, серед яких розв’язання різноманітних інженерно-геометричних задач у машинобудуванні та будівництві для виробів складної форми, вміння моделювати форми, що відповідають вимогам сучасного машинобудування, архітектури і технічної естетики, знання правил технічного документування, вміння розв’язувати інженерні задачі графічними засобами, набуття навичок виконання й читання креслень (уявлення об’єкта за його зображенням).
Роль і значення дисципліни „Інженерна та комп’ютерна графіка” для інженера будь-якої спеціальності важко переоцінити, тому що вона розвиває просторове уявлення людини, образне сприймання навколишнього світу, що лежить в основі будь-якої творчої діяльності. Комп’ютеризація дала новий поштовх розвитку дисципліни, дозволила інженеру не тільки розв’язувати складні інженерні задачі, а й здійснювати пошук оптимального (найкращого) рішення.
Прямокутні проекції основних геометричних тіл
Тема: Вступ. Предмет і задачі інженерної графіки. Методи проектування та основні їх властивості
Лекція – 1а 1 год.
Мистецтво виконання зображень навколишніх предметів є одним із найдавніших. Людина почала виконувати зображення раніше ніж писати.
Історія розвитку людського суспільства нерозривно пов'язана з розвитком мистецтва графічного зображення, яке розвивалось та удосконалювалось одночасно з розвитком живопису, архітектури, мореплавства, кораблебудування і т.і.
Першим систематизованим твором із геометрії (який не дійшов до наших днів) вважається робота Гіппократа Хіоського ( V в. до н.е.). До перших відомих робіт із геометрії відносять роботи Піфагора (530-510 р. до н.е.), Демокріта (460-370 р. до н.е.) і Платона (428-348 р. до н.е.).
Спираючись на праці своїх попередників, Евклід (365-300 р. до н.е.) у своїх 13 книгах «Початки» створив завершену геометричну систему, яка використовується і сьогодні.
Значний вклад у розвиток теорії зображень внесли вчені Леонардо да Вінчі (1452-1519рр.), Дюрер А. (1471-1528рр.), Ж. Дезарг (1593-1662рр.), Р. Декарт (1596-1650рр.) і І. Ламберт (1728-1777рр.). Слід відзначити, що ще Аполлоній з Перги використовував координати, але без координатних чисел. В «Географії» Птоломея (85-168рр.) широта й довгота вже були числовими координатами. Французький учений Г. Монж (1746-1818рр.) уперше систематизував і узагальнив практичні й теоретичні пошуки в галузі зображень просторових форм на площині і дав перший виклад метода виконання креслення у своїй роботі «Нарисна геометрія», яка була видана в 1798 р.
Дані археологічних розкопок, старовинні рукописні книги (їх ілюстрації) та історичні пам'ятники свідчать про самостійність розвитку мистецтва графічних зображень у Київській Русі. Зодчі Київської Русі створили такі всесвітньо відомі пам'ятки архітектури, як Софію Київську, Золоті Ворота, які й зараз викликають захоплення. Правила будівництва були викладені в "Будівельному статуті" та в Руській Правді (1020 р.) Ярослава Мудрого. Там же були наведені зображення, побудовані за проекційним принципом. Креслень зодчих Київської Русі не збереглося, хоч є підстави вважати, що майстри користувалися схематичними рисунками. Винятковий інтерес становить креслення будови, виконане гострим предметом на лесовому грунті біля Десятинної церкви у Києві.
У Росії зі старовинних графічних зображень відомі такі, як "Карта Московии" (1497р.), "Большой чертеж" всієї Московської Русі (1570р.), план м. Пскова (1581р.), "Петров план" Москви (1597р.) та ряд інших. Про високий розвиток мистецтва креслення й застосування проекційних та аксонометричних методів зображення предметів у Росії свідчать креслення: парової машини І.І.Ползунова (1728-1766рр.), одноаркового моста через р. Неву І.П.Кулібіна (1735-1818рр.), креслення архітекторів Д.В.Ухтомського (1719-1774рр.), В.І.Баженова (1738-1799рр.), М.Ф.Казакова (1738-1812рр.) і багатьох інших.
Перший курс нарисної геометрії був прочитаний у 1810 р. в Петербурзькому інституті корпусу інженерів шляхів сполучення французьким інженером К.І.Потьє, учнем Монжа. З 1818 р. в цьому інституті лекції з нарисної геометрії починає читати проф. Я.О.Севастьянов (1796-1849рр.), який в 1821 р. написав перший у Росії оригінальний курс "Основания начертательной геометрии".
Російські вчені М.І.Лобачевський (1792-1856рр.), П.Л.Чебишев (1821-1894рр.), М.І.Макаров (1824-1904рр.), В.І.Курдюмов (1853-1904рр.), Є.С.Федоров (1853-1919рр.) і багато інших у своїх працях заклали основи графічної науки і сприяли її подальшому розвитку в Росії. Послідовниками цього курсу були професори М.О.Ринін (1877-1942рр.) та О.І.Добряков (1895-1947рр.).
Новий етап розвитку нарисної геометрії та інженерної графіки почався в 40-ві роки ХХ ст., коли в Москві проф. М.Ф.Четверухін (1891-1974рр.), а в Києві проф. С.М.Колотов (1880-1965рр.) опублікували ряд наукових праць, які започаткували систематичні наукові та науково-методичні дослідження в цій галузі знань.
Професор І.І.Котов (1909-1976рр.) перший застосував апарат нарисної геометрії до розв'язування прикладних задач у різних галузях техніки. Він розробив також основні принципи застосування ЕОМ у курсі нарисної геометрії, заснувавши московський семінар "Кібернетика графіки".
Сьогодні великий вклад у розвиток викладання нарисної геометрії й креслення у вузах України вносить київська школа геометрів під керуванням проф. В.Є.Михайленка, учня Колотова. При їх активній участі на багатьох кафедрах провідних вузів успішно розробляється напрямок геометричного моделювання, або інженерної геометрії, коли за наперед заданими умовами та вимогами формуються оптимальні геометричні моделі майбутнього виробу.
Нарисна геометрія – це наукова дисципліна, яка вивчає способи побудови точного зображення просторових форм на площині, розглядає графічні методи розв'язання геометричних задач і розкриває геометричні властивості просторових форм. Такі зображення прийнято називати креслениками. Кресленики мають велике значення в усіх галузях виробництва, тому що за їх допомогою можна взнати не тільки форму предмета, але й усі його розміри, взаємне розміщення окремих частин і навіть матеріал, із якого він виготовлений.
За допомогою креслення можна передати свої думки, ідеї та уявлення як про існуючі просторові форми, так і про нові, які виникають у процесі творчої праці інженера.
Основні правила та методи побудови зображень і вивчає нарисна геометрія.
Предметом нарисної геометрії є розробка методів побудови та читання креслеників, способів розв'язування геометричних задач, методів геометричного моделювання, тобто створення проекцій предмета, який відповідав би наперед заданим геометричним та іншим вимогам, а також побудова зображень предметів та об'єктів деякої конкретної галузі інженерної діяльності
Тому ціллю предмета нарисної геометрії є:
- розвиток просторової уяви;
- розвиток здібностей до аналізу та синтезу просторових форм;
- вироблення навиків необхідних для виконання та читання технічних креслень;
- знайомство з засобами механізації та автоматизації графічних робіт.
Комп’ютеризація усіх форм діяльності, зокрема широке застосування ЕОМ, дисплеїв та графозображувачів, показала принципову можливість виконання креслень і графічних побудов за допомогою електронних апаратів. В основі машинної графіки, за допомогою якої можуть виконуватись одноманітні, трудомісткі операції або складні розрахунки, лежать обчислювальна геометрія, системи алгоритмів, програм, використання графічних мов тощо. Абсолютно очевидно, що машинна графіка як одна з підсистем САПР може розвиватись лише на основі широкого використання законів і правил нарисної геометрії та інженерної графіки.
Для побудови зображення будь-якого об’єкта необхідно мати геометричний простір та формоутворюючі елементи простору. Геометричним простором сучасна геометрія називає сукупність однорідних об’єктів (фігур). Формоутворюючими елементами простору є геометричні фігури, які можна представляти будь-якими множинами точок. Геометричних фігур дуже багато, але до основних можна віднести лише три: точку, пряму і площину, з яких утворюються більш складні фігури.
В основу методу нарисної геометрії покладений метод проекцій, який дозволяє отримувати відображення просторових фігур на площині або поверхні. Згідно з цим методом, кожній точці тривимірного простору ставиться у відповідність точка двовимірного простору (площини) (рис.1).
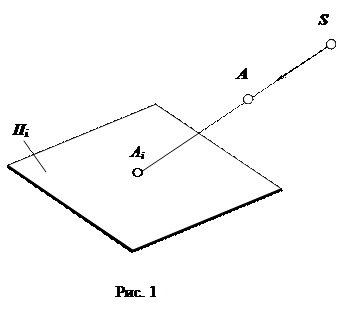
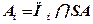
Точка S називається центром проектування, напрямок SA – проектуючим променем, площина Пi – площиною проекцій і точка Аi – проекцією точки А на площину проекцій Пi
Метод проекцій включає два випадки:
 1 Центральнее проектування
1 Центральнее проектування
При центральному проектуванні проектуючі промені (рис. 2) виходять з однієї точки – центра проектування S, який знаходиться на визначеній (заданій) відстані від площини проекцій Πi.
| |
Для побудови центральної проекції miкривої лінії m необхідно вибрати на цій лінії деяку кількість точок, побудувати їх проекції і з'єднати відповідною лінією (рис. 2). При центральному проектуванні кривої лінії проектуючі промені утворюють у просторі конічну поверхню, тому цей вид проектування і має іншу назву – конічне проектування.
Центральне проектування – найбільш загальний випадок проектування геометричних образів на площину. Основними і незмінними його властивостями (інваріантами) є такі:
– проекцією точки є точка;
– проекцією прямої є пряма ( в частковому випадку – точка);
– якщо точка належить прямій, то проекція цієї точки належить проекції прямої.
Однією з особливостей центрального проектування є його достатня наочність, оскільки воно відповідає природньому зоровому сприйняттю людиною навколишніх предметів і тому найбільш широке застосування цей вид проектування одержав при виконанні перспективних зображень в архітектурі.
Основний його недолік – складність у визначенні дійсних розмірів предмета по його зображенню.
2. Паралельне проектування
 Паралельне проектування можна розглядати як частковий випадок центрального, коли центр проектування S знаходиться в нескінченності. При цьому проектуючі промені паралельні між собою (рис. 3) і тому інша назва цього виду проектування – циліндричне проектування. Апарат паралельного проектування включає в себе площину проекцій Πi та напрямок проектування s, який задається кутом φнахилу проектуючого променя до площини проекцій. Залежності від значення кута φпаралельне проектування може бути косокутним (φ≠90°), або прямокутним(φ=90°).
Паралельне проектування можна розглядати як частковий випадок центрального, коли центр проектування S знаходиться в нескінченності. При цьому проектуючі промені паралельні між собою (рис. 3) і тому інша назва цього виду проектування – циліндричне проектування. Апарат паралельного проектування включає в себе площину проекцій Πi та напрямок проектування s, який задається кутом φнахилу проектуючого променя до площини проекцій. Залежності від значення кута φпаралельне проектування може бути косокутним (φ≠90°), або прямокутним(φ=90°).
Основні властивості паралельного проектування:
1. Проекцією точки є точка.
2. Проекцією прямої є пряма (в частковому випадку - точка).
3. Якщо точка належить прямій, то і проекція точки належить проекції прямої.
4. Якщо прямі паралельні, то і їх проекції паралельні між собою.
5. Відношення відрізків прямої дорівнює відношенню проекцій цих відрізків.
6. Відношення відрізків паралельних прямих дорівнює відношенню проекцій цих відрізків.
7. Проекція геометричної фігури не змінює своєї величини і форми при паралельному переміщенні площини проекцій.
8. Точка перетину проекцій прямих, що перетинаються є проекцією точки перетину цих прямих.
Прямокутне (або ортогональне) проектування, крім наведених вище, характеризується ще такими властивостями:
1. Проекція відрізка не може бути більше самого відрізка.
Частковий випадок. Якщо відрізок паралельний площині проекцій, то він проектується на неї в натуральну величину.
Питання для самоконтролю
1.Які завдання ставляться перед курсом нарисної геометрії?
2.На якому методі ґрунтується курс нарисної геометрії?
3. У чому різниця між центральним і паралельним проектуванням?
4. Чи може при центральному і паралельному проектуванні лінія зображатися точкою, а площина – прямою?
Прямокутні проекції основних геометричних тіл
Тема: Визначеність зображень. Прямокутні проекції. Комплексне креслення Монжа. Точка, пряма, площина загального і часткового положення на епюрі Монжа
Лекція – 1б 1 год.
Відомо, що проекційні зображення, які використовуються в технічній документації, повинні відповідати таким основним вимогам:
– бути оберненими (метрично визначеними), тобто такими, щоб за ними можна було визначити форму і розміри зображеного предмета;
– бути наочними, тобто такими, щоб за ними можна було уявити зображений предмет і його положення в просторі;
– бути відносно простими у графічному виконанні.
Розглянуті методи проектування на одну площину проекцій дають можливість розв'язувати пряму задачу – маючи предмет, знайти його проекцію, але не дозволяє розв'язати обернену задачу – маючи проекцію, визначити форму і розміри предмета. Наприклад, маючи проекцію Ai (рис. 1), не можна визначити положення самої точки A в просторі, оскільки невідома її відстань від площини проекцій Πi.
Наявність лише однієї проекції створює невизначеність зображення. Такі зображення повинні містити додаткові дані, щоб за ними можна було визначити оригінал.
Розглянемо деякі способи доповнення зображень геометричних образів при паралельному проектуванні.
На практиці найбільш широке застосування набули чотири способи доповнення однопроекційного зображення: проекції з числовими відмітками; векторіальні (федоровські) проекції; аксонометричні проекції; прямокутні проекції.
Проекції з числовими відмітками. Цей метод зображень ґрунтується на тому, що для кожної точки предмета на площині проекцій додатково вказують величину її відстані (при визначених одиницях виміру) від заданої площини проекцій. Цю відстань називають числовою відміткою точки. Креслення з числовими відмітками використовують в основному в картографії, при проектуванні доріг і т. п.
Векторіальні (федоровські) проекції названі на честь академіка Є.С.Федорова, який запропонував зображати висоти точок предмета за допомогою паралельних відрізків. Початок відрізка – в проекції відповідної точки. Довжина відрізка дорівнює висоті точки. Цей метод зображення застосовується у кристалографії, геології і т. п.
Аксонометричні проекції більш детальніше розглядаються в окремій лекції. Тут можна лише відзначити, що зображенням, отриманим за допомогою методу аксонометричних проекцій, притаманна більша наочність, але вони і більш трудомісткі при виконанні.
Прямокутні проекції найбільше застосовуються при виконанні технічних креслень, тому що в цьому випадку забезпечується простота графічних побудов і висока точність вимірів. Основний недолік цього методу – недостатня наочність зображення: для того, щоб “побачити” (уявити) предмет, необхідно подумки поєднати його наявні “плоскі” зображення.
 Метод прямокутних проекцій ґрунтується на тому, що предмет за допомогою ортогонального (прямокутного) проектування одночасно зображають на декількох взаємноперпендикулярних площинах проекцій, приєднаних до просторової прямокутної системи координат.
Метод прямокутних проекцій ґрунтується на тому, що предмет за допомогою ортогонального (прямокутного) проектування одночасно зображають на декількох взаємноперпендикулярних площинах проекцій, приєднаних до просторової прямокутної системи координат.
Розглянемо дві взаємно-перпендикулярні площини, які ділять простір на 4 частини, що називаються четвертями або квадрантами (рис.4). Така модель називається двох-площинною. Відповідно площина П1 називається горизонтальною площиною проекцій, а П2 - фронтальною площиною проекцій.
При двох напрямах проектування, що прийняті в системі прямокутних проекцій, довільна точка А зображується парою точок ( А1- горизонтальна проекція, А2 – фронтальна проекція ). Неважко помітити, що точка простору віддалена від площин проекцій П1 та П2 на відстань від осі відповідно до її фронтальної та горизонтальної проекцій. Креслення, що містить проекції на двох полях проекцій, позиційно повне та метрично визначене.
 Однак, завдяки тривимірності просторової фігури, а також у зв’язку з тим, що по двох зображеннях не завжди просто визначити конструкцію складного об’єкта, його комплексне креслення стає зрозумілішим, коли крім двох основних проекцій дано ще проекцію на третю площину. В ролі третьої площини (поля проекцій) найчастіше вибирають профільну площинупроекцій П3 , перпендикулярну до П1 та П2 (рис.5), тому третя проекція точки А3 називається профільною. Така модель називається трьох площинною.
Однак, завдяки тривимірності просторової фігури, а також у зв’язку з тим, що по двох зображеннях не завжди просто визначити конструкцію складного об’єкта, його комплексне креслення стає зрозумілішим, коли крім двох основних проекцій дано ще проекцію на третю площину. В ролі третьої площини (поля проекцій) найчастіше вибирають профільну площинупроекцій П3 , перпендикулярну до П1 та П2 (рис.5), тому третя проекція точки А3 називається профільною. Така модель називається трьох площинною.
При побудові комплексного креслення або епюра Монжа з трьох прямокутних проекцій площину П2приймають нерухомою, а площини П1 та П3 суміщують з нею обертанням навколо осей xта z.
Площини /поля/ проекцій П1, П2та П3, перетинаючись по трьох лініях, задають просторову декартову систему координат (рис.5). Точка Оє початком координат, вісь х - віссю абсцис, вісь у - віссю ординат та вісь z- віссю аплікат. Неважко помітити, що проекції А1 та А2 лежать на одній вертикальній лінії, а проекції А2 та А3 – на одній горизонтальній лінії, які називаються лініями зв’язку.
 Розглянемо, якою лінією зв’язку можна з’єднати проекції А1 та А3.
Розглянемо, якою лінією зв’язку можна з’єднати проекції А1 та А3.
Для цього розглянемо квадрат О, А31, АО, А13 (рис.6 ). Діагональ цього квадрата - бісектриса кута у(-z), О, у(-x). Лінія зв’язку, яка з’єднує про-екції А1 та А3 - ламана, що складається з двох відрізків горизонтального та вертикального) з вершиною на бісектрисі к кута у(-z), О, у(-x). Частину цієї ламаної інколи замінюють дугою кола. Таким чином, між горизонтальною та профільною проекціями існує ламана горизонтально-вертикальна лінія зв’язку. Бісектрису к, що є множиною вершин цих ламаних ліній, називають постійною прямою комплексного креслення.
Площини проекцій П1, П2 та П3ділять тривимірний простір на вісім частин, які називаються октантами. У тих випадках, коли точка задається координатами, можна будувати комплексне креслення, керуючись величиною та знаками координат, навіть не визначаючи октанту, в якому задана точка.
Знаки координат, які відповідають тому чи іншому октанту, наведені в таблиці 2. Таблиця 2
| Октанти | ||||||||
| x | + | + | + | + | - | - | - | - |
| y | + | - | - | + | + | - | - | + |
| z | + | + | - | - | + | + | - | - |
Якщо точка знаходиться в першій чверті (двох площинна модель) або в першому (п’ятому) октанті (трьох площинна модель) простору при закріплених площинах проекцій, то її горизонтальна проекція розміщується нижче, а фронтальна проекція – вище х. По-іншому розміщуються проекції точок, що перебувають в 2(6),3(7)та 4(8) чвертях (октантах) простору. На рис.7 показано розташування точок у різних чвертях простору.
Якщо одна з проекцій точки розміщена на осі, то точка простору належить одній із площин проекцій і розташована на границі чвертей.
 |
Якщо відстані від проекцій точок до осі рівні, то точка простору належить бісекторній площині. Бісекторна площина – це площина , яка ділить четверті навпіл. Площина, яка проходить через 1 і 3 четверті називається 1ою бісекторною площиною і позначається буквою К, площина, яка проходить через 2 і 4 чверті – 2оюбісекторною площиною і позначається буквою U.
Приклад 1.
 |
Побудувати комплексне креслення точок А(-30,-20,40) та В(10,30,-10) і визначити октанти простору, в яких вони розташовані.
Користуючись таблицею 2, легко визначити, що точка А задана в 6 октанті, а точка В – в 4. Комплексне креслення точок приведене на рис. 8.
У практичних додатках користуються, як правило, 1 чвертю, тому подальший матеріал буде подаватися стосовно неї.
Питання для самоконтролю.
1. Чим різняться між собою двоплощинна та триплощинна моделі простору?
2. Якщо точка простору належить площині П2, як будуть розташовані її проекції?
3. Як зобразяться проекції точки, що належить бісекторній площині в 3 і 4 чвертях простору?
Прямокутні проекції основних геометричних тіл
Тема: Прямокутні проекції. Проекції прямої. Проекції площини.
Лекція – 2а 1год.
Пряму в нарисній геометрії розглядають як множину точок; її проекції в загальному випадку також прямі. В системі площин П1 та П2пряма загального положення зображається двома прямими. Оскільки дві точки визначають будь-яку пряму, то при рішенні практичних задач часто пряму задають відрізком.
По відношенню до площин проекцій пряма може займати як загальне, так і часткове положення.
Пряма, яка не паралельна жодній з площин проекцій, називається прямою загальногоположення.
На рис. 9 представлена пряма загального положення.
 Точки перетину прямої з площинами проекцій називають слідами прямої.
Точки перетину прямої з площинами проекцій називають слідами прямої.
Горизонтальний слід (Н) – точка перетину з горизон-тальною площиною про-екцій.
Н1 і Н2 – відповідно горизонтальна проекція горизонтального сліду і фронтальна проекція горизонтального сліду.
Фронтальний слід
(F) – точка перетину з фронтальною площиною проекцій. F1 і F2 – відповідно горизонтальна проекція фронтального сліду та фронтальна проекція фронтального сліду.
 На рис. 10 показаний епюр прямої та послідовність знаходження її слідів.
На рис. 10 показаний епюр прямої та послідовність знаходження її слідів.
Прямі часткового положення це прямі, які паралельні або перпендикулярніплощинам проекцій.
 |
Прямі, паралельні площинам проекцій, належать до так званих прямих рівня і називаються АС – горизонтальною (рис.11а ), АВ - фронтальною (рис.11б), АМ - профільною прямими (рис.11в). Відрізки прямих зображуються в натуральну величину на площині проекцій, якій вони паралельні.
Прямі, перпендикулярні до площин проекцій, називають проектуючими: АК – горизонтально– проектуюча або вертикальна (рис. 12а ), АР – фронтально-проектуюча (рис.12б), АТ – профільно-проектуюча (рис.12в). Такі прямі зображуються точкою на площині проекцій, до якої вони перпендикулярні. При цьому вони паралельні двом іншим площинам проекцій.
 |
При розгляді відрізка прямої часто виникає потреба у визначенні його натуральної величини та кутів нахилу до площин П1 та П2, тобто доводиться розв’язувати першу основну метричну задачу. Справді, відстань між двома фігурами вимірюється відстанню між найближчими точками цих фігур.
 Для визначення натуральної величини відрізка прямої загального положення треба виконати деякі побудови.
Для визначення натуральної величини відрізка прямої загального положення треба виконати деякі побудови.
На рис.13 показано відрізок АВ та дві площини проекцій П1 та П2.
 Якщо з точки А провести відрізок АС, паралельний його горизонтальній проекції А1В1, то утвориться прямокутний трикутник АВС, гіпотенуза якого – відрізок АВ. Розглянувши цей трикутник, можна зробити висновок, що натуральна величина відрізка прямої загального положення дорівнює гіпотенузі прямокутного трикутника, один катет якого – одна з проекцій відрізка, а другий – різниця відстаней кінців другої проекції відрізка до осі. Відповідну побудову виконано на рис.14.
Якщо з точки А провести відрізок АС, паралельний його горизонтальній проекції А1В1, то утвориться прямокутний трикутник АВС, гіпотенуза якого – відрізок АВ. Розглянувши цей трикутник, можна зробити висновок, що натуральна величина відрізка прямої загального положення дорівнює гіпотенузі прямокутного трикутника, один катет якого – одна з проекцій відрізка, а другий – різниця відстаней кінців другої проекції відрізка до осі. Відповідну побудову виконано на рис.14.
Одночасно визначається і кут a нахилу прямої до горизонтальної площини проекції П1. Щоб знайти кут нахилу прямої до фронтальної площини проекцій, відповідну побудову треба виконати на полі П2. Цей спосіб визначення величини відрізка прямої називають способом прямокутного трикутника.
Якщо точка є нульвимірною геометричною фігурою, пряма – одновимірною, то площина – двовимірна геометрична фігура.
Задавати площину можуть три точки, що не лежать на одній прямій, дві паралельні прямі, дві прямі, що перетинаються, точка і пряма (точка не належить прямій), будь-яка плоска фігура та сліди площини (рис. 15 ).

 Сліди площини – це лінії перетину площини з площинами проекцій. Задання площини її слідами - найпростіший спосіб задання. На рис. 16 площину задано точкою сходу слідів на осі х, а також кути, які сліди утворюють з віссю x.
Сліди площини – це лінії перетину площини з площинами проекцій. Задання площини її слідами - найпростіший спосіб задання. На рис. 16 площину задано точкою сходу слідів на осі х, а також кути, які сліди утворюють з віссю x.
Площини не паралельні та не перпендикулярні площинам проекцій називаютьсяплощинами загального положення.
Площини – перпендикулярні площинам проекцій є площинами часткового положення і називаються проектуючими. Площина, перпендикулярна до горизонтальної площини проекцій називається горизонтально-проектуючою (рис.17а). Площина, перпендикулярна до фронтальної площини проекцій, називається фронтально-проектуючою (рис.17б). А площина, перпендикулярна профільній площині проекцій, є профільно-проектуючою (рис. 17в).

Площини, паралельні площинам проекцій, називаються площинами рівня. Відсіки площин рівня на відповідних площинах проекцій зображуються в натуральну величину. Площина, паралельна горизонтальній площині проекцій, називається горизонтальною (рис.18а), площина, паралельна фронтальній площині проекцій, називається фронтальною (рис. 18б), площина паралельна профільній площині проекцій – профільна площина рівня (рис. 18в).
Питання для самоконтролю
1. Що називається слідами прямої?
2. Що називається прямими рівня?
3. Як виглядають проекції проектуючих прямих?
4. Чим можна задати проекції площини?
Взаємне положення геометричних фігур
Тема: Позиційні задачі. Взаємна належність точок, прямих і площин. Перетин прямих і площин. Сліди прямої і площини.
Лекція –2б 1 год.
У нарисній геометрії розглядаються дві групи задач: позиційні та метричні, в основу яких покладено позиційні та метричні властивості пар їх проекцій.
Позиційні задачі – це задачі на визначення загальних елементів різних геометричних фігур (належність, перетин тощо).
1.1 Точка і пряма
 |
Точка може належати або не належати прямій. Для розв'язку питання про належність досить розглянути їх проекції, прийнявши до уваги таку властивість: точка належитьпрямій, якщо її проекції належать тим же проекціям прямої, і не належить прямій, коли хочаб одна з її проекцій не належить тій же проекції прямої.
На рис. 19 показано прямі а та в.

Точка А, проекції якої належать відповідним проекціям прямої а, належить цій прямій. Точка Сне належить прямій в, бо її горизонтальна проекція не належить горизонтальній проекції прямої.
Для двох проекцій (фронтальної та горизонтальної) профільної прямої умови належності недостатні, бо якщо пряма і точка належать одній профільній площині, то проекції точки завжди належать проекціям прямих. У цьому випадку треба внести однозначність, яка полягає в тому, що профільна проекція точки повинна належати профільній проекції прямої, або, що аналогічно, повинна своїми проекціями ділити проекції довільно зафіксованого на прямій відрізка в одному й тому ж відношенні (рис.20 ).
 |
1.2 Дві прямі
Прямі можуть перетинатися, якщо мають одну власну чи невласну спільну точку, або бути мимобіжними, якщо вони не мають спільної точки.
Дві прямі в просторі в загальному положенні мимобіжні. В цьому випадку, як відомо, через них можна провести одну пару площин, паралельних площині паралелізму (це площина, паралельна двом мимобіжним прямим), яку можна задати, якщо через довільну точку простору провести дві прямі, паралельні цим мимобіжним.
Сформулюємо властивості: якщо точки перетину однойменних проекцій прямих належать одній вертикальній лінії зв’язку, прямі перетинаються (рис.21а); якщооднойменні проекції прямих паралельні між собою (мають невласну точку перетину), пряміпаралельні (рис. 21 б); якщо точки перетину однойменних проекцій прямих не належать одній вертикальній чи горизонтальній лінії зв’язку, прямі мимобіжні (рис. 22).


Звернемося до рис. 22, де зображено дві мимобіжні прямі. Фронтальні проекції перетинаються в точці 12=22, а горизонтальні - в точці 31=41.
Ці точки називаються конкуруючими. Конкуруючі точки (точки, що належать одній проектуючій прямій) використовують при визначенні видимості геометричних фігур.
Для визначення "перекривання" їх на проекціях візьмемо конкуруючі точки 12=22 відносно поля П2, точки 31=41 відносно поля П1. Завдяки тому, що точка 3 розміщена вище точки 4, на полі П1 пряма s "перекриває" пряму t. Точка 1 розміщена ближче точки 2, тому на полі П2 пряма s "перекриває" пряму t.
Пряма та площина
 |
Пряма належить площині, якщо дві її точки належать площині (рис.23 а) або коли вона проходить через точку, що належить площині, та паралельна другій прямій що належить площині (рис. 23 б). Для задання прямої, що належить площині, досить задати її горизонтальну чи фронтальну проекцію.
Крім того, є лінії, що належать площині і займають часткове положення. До таких ліній можна віднести лінії рівня та лінії найбільшого нахилу площини до площин проекцій.
 |
Лініями рівня площини називають лінії, що належать даній площині та паралельні одній з площин проекцій. Горизонталь - це лінія, що належить площині та паралельна П1.
На рис. 24а проведено горизонталь АВ. Фронталь - лінія, що лежить у площині та паралельна П2. На рис. 24 б проведено фронталь f. Горизонталь та фронталь часто використовуються при заданні площини, що дозволяє виявити її орієнтацію відносно площин проекцій. Сліди площини також є крайніми положеннями горизонталі h чи фронталі f, їх в цьому випадку називають нульовими (рис. 24б ).

Профільна пряма - лінія, що належить площині та паралельна профільній площині проекцій П3.
Лінії найбільшого нахилу площини до площин проекцій - лінії, що належать площині та утворюють найбільший кут з відповідною площиною проекцій. Зокрема, по відношенню до поля П1, їх ще називають лініями найбільшого скату. Лінія найбільшого нахилу до площини П1 утворює прямий кут з проекцією горизонталі (рис. 25 а), а лінія найбільшого нахилу до площини П2 – прямий кут з фронтальною проекцією фронталі (рис. 25 б).
Також пряма може перетинати площину або бути їй паралельною, тобто перетинати у невласній точці. Задача на перетин прямої з площиною вважається першою основноюпозиційною задачею. При розв’язанні цієї задачі розрізнятимемо три різних випадки розміщення двох геометричних елементів: а) обидва геометричні елементи є проектуючими щодо однієї і тієї ж площини проекцій; б) один геометричний елемент – проектуючий, другий - загального положення; в) обидва геометричні елементи займають загальне положення. На рис. 26 а показано перший випадок, коли площина - трикутний відсік АВСта пряма lзаймають горизонтально проектуюче положення. Горизонтальна проекція трикутного відсіку ніби збирає на себе проекції усіх фігур, що належать площині відсіку. Належність горизонтальних проекцій відсіку та прямої дозволяє стверджувати, що в цьому випадку пряма lналежить площині відсіку.

На рис. 26 б показано другий випадок, коли площина у вигляді трикутного відсіку перебуває в горизонтально-проектуючому положенні, а пряма l займає загальне положення. В цьому випадку точка 2 перетину прямої з площиною визначається безпосередньо на полі П1, як точка перетину проекцій прямої та площини; фронтальна проекція точки 2визначається за вертикальною відповідністю. 3 метою підвищення наочності рисунка вважаємо трикутний відсік непрозорим і тоді частина відрізка прямої буде невидимою, бо він "перекривається" на полі П2, площиною. Позначимо на полі П2 точку перетину прямої lіз стороною відсіку A2B2, за допомогою вертикальної лінії зв’язку визначимо точку 11 на прямій та точку 31 - на площині. Оскільки точка 1 ближче до спостерігача, ніж точка 3, пряма в цій точці "перекриває" сторону A2B2, і тому відрізок прямої до точки перетину з площиною видимий, а далі частина його закривається площиною.
 На рис. 27 зображено третій випадок, коли і площина, і пряма займають загальне положення. Для визначення точки перетину прямої з площиною в цьому випадку доцільно застосувати допоміжну площину, яка проходить через пряму і є проектуючою по відношенню до однієї з площин проекцій. Алгоритм розв’язання задачі складається з трьох операцій: І) через пряму проводять допоміжну площину; 2) знаходять лінію перетину заданої площини з допоміжною; 3) визначають точку перетину двох прямих - заданої та лінії перетину.
На рис. 27 зображено третій випадок, коли і площина, і пряма займають загальне положення. Для визначення точки перетину прямої з площиною в цьому випадку доцільно застосувати допоміжну площину, яка проходить через пряму і є проектуючою по відношенню до однієї з площин проекцій. Алгоритм розв’язання задачі складається з трьох операцій: І) через пряму проводять допоміжну площину; 2) знаходять лінію перетину заданої площини з допоміжною; 3) визначають точку перетину двох прямих - заданої та лінії перетину.
На рисунку 27 через пряму проведено горизонтально -проектуючу площину Г, знайдено лінію перетину двох площин - пряму 1-2 (її горизонтальна проекція 1121), за горизонтальною проекцією визначено фронтальну проекцію 1222. В перетині l2та 1222 знайдено шукану точку К2 - перетин прямої з площиною (її горизонтальна проекція визначається за вертикальною лінією зв’язку). Видимість відрізків прямої l визначена за допомогою конкуруючих точок 3,4. Пряма може перетинати площину в невласній точці, тобто бути паралельною площині. В такому випадку (рис. 28) проекція лінії перетину площини з допоміжною площиною 1222 паралельна проекції прямої l2.
Тобто, пряма паралельна площині, якщо вона паралельна будь-якій прямій, що лежить у цій площині.
 |
Точка та площина
 |
Точка може належати площині або не належати їй. Це визначається за допомогою прямої, що належить площині.
На рис. 29 показано трикутний відсік АВС ізадано точки 1 та 2. Точка 1 належить площині, бо вона належить прямій ВD, що є підмножиною площини; точка 2 не належить площині, бо тільки фрональна проекція її належить фронтальній проекції прямої – В2D2, а горизонтальна проекція не належить В1D1. Звідси можна сформулювати таку властивість.: точка належить площині, якщо обидві її проекції збігаються з тими самими проекціями прямої, що належить площині.
1.5 Дві площини
Якщо дві площини не співпадають, то вони завжди перетинаються. Якщо лінія їх перетину - невласна пряма, то площини паралельні. Тому, щоб з’ясувати взаємне положення двох площин, знаходять лінію їх перетину, що є другою головною позиційною задачею.
Як і при розв’язанні першої головної позиційної задачі, тут спостерігаються ті ж самі три випадки: а) обидві площини є проектуючими відносно однієї й тієї ж площини проекцій; б) одна з площин - проектуюча, друга - загального положення; в) обидві площини загального положення.

На рис. 30 а показано два вертикальні трикутні відсіки. Перетин їх горизонтальних проекцій визначає вертикальну лінію перетину двох площин, яка за відповідністю визначається на полі П2.
На рис. 30 б одна з площин, що перетинаються, займає загальне положення, а друга – горизонтально-проектуюча. Лінія взаємного перетину площин у цьму випадку збігається на полі П1 з горизонтальною проекцією проектуючого відсіку - це пряма 1121. За вертикальною відповідністю визначається фронтальна проекція лінії перетину двох площин.
 |
На рис. 31 показано визначення лінії перетину двох відсіків загального положення. Лінію перетину визначено за точками перетину двох сторін одного відсіку з площиною другого, що є 2 рази розв’язана перша позиційна задача. З цією метою через пряму С2В2проведено фронтально-проектуючу площину Ф2, а через пряму С2А2 - фронтально- проектуючу площину. На цих двох прямих знайдено точки перетину їх з площиною, які й визначать лінію перетину двох площин.
Коли лінія перетину двох площин - невласна пряма, то площини паралельні між собою. Ознакою паралельності є паралельність двох прямих однієї площини двом прямим другої, найчастіше це горизонталі та фронталі площин (сліди). На рис. 32 показано дві паралельні площини. Одну задано слідами, а другу - трикутним відсіком АВС; сторона відсіку АВ є фронталлю,
 |
а АС - горизонталлю площини.
Питання для самоконтролю.
Взаємне положення геометричних фігур
Тема: Метричні властивості пар геометричних елементів
Лекція – 3 2 год.
Метричні задачі – це задачі на визначення значень геометричних величин (довжин відрізків, кутів, відстаней).
Різновидів метричних задач багато, але кожен з них включає в себе дві основні метричні задачі: перша - на визначення відстані між двома точками - була розглянута раніше; друга полягає у проведенні перпендикуляра до площини. На основі вказаних задач можна розв’язати будь-яку метричну задачу.
Точка та пряма
При частковому положенні прямої відстань від точки до прямої може проектуватися на одну із площин проекцій у натуральну величину. Це можливо за таких умов:
 |
а) відстань від точки до прямої проектується в натуральну величину на горизонтальній проекції, якщо пряма горизонтально-проектуюча, і на фронтальній, якщо пряма фронтально- проектуюча. На рис. 33 а показано вертикальну пряму вта точку А. Відстань між прямою і точкою зобразиться без спотворення на полі П1;
Рис. 33
б) відстань від точки до прямої проектується в натуральну величину на горизонтальній проекції, якщо площина, що задана точкою та прямою - горизонтальна, і на фронтальній проекції, якщо ця площина фронтальна. На рис. 33 б показано пряму а та точку В, що задають фронтальну площину. Відстань від точки до прямої зобразиться без спотворення на полі П2.
Для визначення відстані від точки до прямої загального положення треба виконати такі побудови. Через точку А проводять площину перпендикулярну до прямої с (рис. 34 ). Знаходять точку перетину прямої с з цією площиною і з’єднують цю точку з точкою А. Одержаний відрізок АВ є проекціями відстані від точки до прямої. Для знаходження натуральної величини відстані можна скористатися методом прямокутного трикутника. Відрізок А0В2 – шуканий.
1.2 Дві прямі
 На підставі властивостей, що стосуються відстані між точкою та прямою, формулюються властивості, які характеризують відстань між паралельними прямими. В частковому випадку:
На підставі властивостей, що стосуються відстані між точкою та прямою, формулюються властивості, які характеризують відстань між паралельними прямими. В частковому випадку:
а) відстань між паралельними прямими проектується в натуральну величину на горизонтальній проекції, якщо прямі горизонтально-проектуючі, і на фронтальній, якщо прямі фронтально-проектуючі (рис. 35 а ).
б) відстань між паралельними прямими зображається в натуральну величину на горизонтальній проекції, якщо задана ними площина горизонтальна, і на фронтальній, якщо ця площина фронтальна (рис. 35 б).
 |
Відстань між двома паралельними прямими загального положення знаходиться за аналогією із визначенням відстані від точки до прямої, якщо на одній із прямих взяти довільну точку, наприклад А.
Дві прямі, що перетинаються, або мимобіжні прямі утворюють між собою кут. Кут між мимобіжними чи прямими, що перетинаються, проектується в натуральну величину на горизонтальній проекції, якщо прямі горизонтальні, і на фронтальній, якщо вони фронтальні (рис. 36 а).
 |
Розглянемо взаємну перпендикулярність двох прямих. Прямий кут перетину чимимобіжності проектується у натуральну величину на горизонтальній проекції, якщо хоча б одна його сторона горизонтальна, та на фронтальній, якщо хоча б одна його сторона фронтальна. На рис. 36 б показано прямий кут перетину, одна сторона якого горизонтальна. Цей кут зображається на полі П1в натуральну величину.
Пряма та площина
Метричні характеристики комбінації (пряма та площина) стосуються визначення відстані між прямою і паралельною їй площиною, а також кута між прямою і площиною, якщо пряма і площина непаралельні.
Відстань від прямої до паралельної їй площини проектується в натуральну величину на горизонтальній проекції, якщо площина горизонтально-проектуюча, та на фронтальній, якщо вона фронтально-проектуюча. На рис. 37а показано відстань між вертикальною площиною К та прямою а.

Кут між прямою та площиною проектується в натуральну величину на горизонтальній проекції, якщо площина горизонтально-проектуюча, а пряма горизонтальна, та на фронтальній проекції, якщо площина фронтально-проектуюча, а пряма фронтальна. На рис. 37б показано кут між фронтально- проектуючою площиною Р та фронтальною прямою в.
Пряма перпендикулярна до площини, якщо вона перпендикулярна до двох прямих, що перетинаються та належать площині. Беручи до уваги властивості проекцій прямого кута, з усієї множини прямих площини за такі лінії доцільно вибрати лінії рівня, тобто горизонталь та фронталь.
 |
 На рис. 38 показано трикутний відсік, сторона якого АСє горизонталлю, а АВ - фронталлю. Щоб з точки Копустити перпендикуляр на площину цього відсіку, досить провести фронтальну проекцію його перпендикулярно до фронтальної проекції фронталі А2В2,а горизонтальну - перпендикулярно до горизонтальної проекції горизонталі А1С1. Звідси: проекція прямої, перпендикулярної до площини, на горизонтальній проекції площини перпендикулярна до проекції горизонталі, на фронтальній - перпендикулярна до проекції фронталі площини.
На рис. 38 показано трикутний відсік, сторона якого АСє горизонталлю, а АВ - фронталлю. Щоб з точки Копустити перпендикуляр на площину цього відсіку, досить провести фронтальну проекцію його перпендикулярно до фронтальної проекції фронталі А2В2,а горизонтальну - перпендикулярно до горизонтальної проекції горизонталі А1С1. Звідси: проекція прямої, перпендикулярної до площини, на горизонтальній проекції площини перпендикулярна до проекції горизонталі, на фронтальній - перпендикулярна до проекції фронталі площини.
Точка та площина
Відстань від точки до площини проектується в натуральну величину на горизонтальній проекції, якщо площина горизонтально-проектуюча, та на фронтальній, якщо площина фронтально-проектуюча. На рис. 39 а показано точку А та вертикальну площину Ф, відстань між якими проектується без спотворення на горизонтальній площині проекцій.
Для визначення відстані від точки до площини загального положення необхідно з точки опустити перпендикуляр до площини та знайти його основу. На рис. 39 б показано трикутний відсік, сторона АСякого - горизонталь, а сторона АВ - фронталь. З точки D проведено проекції перпендикуляра n, його горизонтальна проекція перпендикулярна до горизонталі на полі П1,а фронтальна проекція перпендикулярна до фронталі на полі П2. Основу перпендикуляра визначено січною горизонтально-проектуючою площиною Г, яка перетне відсік по прямій 1-2. Основа перпендикуляра - точка Е, а проекції - відстані від точки до площини D1E1та D2E2. Натуральна величина відрізка DE знайдена за допомогою методу прямокутного трикутника.

1.5 Дві площини
Розглянемо метричні характеристики (відстані та кути) між двома площинами. Відстань між паралельними площинами проектується в натуральну величину на поле П1, якщо площини горизонтально-проектуючі, та на поле П2, якщо площини фронтально-проектуючі. На рис. 40 а показано відстань між двома паралельними вертикальними площинами Фта Т , що проектується без спотворення на поле П1. Кут між двома площинами (двогранний кут) проектується в натуральну величину на полі П1, якщо площини горизонтально-проектуючі, та на П2 - якщо вони фронтально-проектуючі.
 На рис. 40б зображено дві фронтально-проектуючі площини, кут між якими зображається без спотворення на полі П2.
На рис. 40б зображено дві фронтально-проектуючі площини, кут між якими зображається без спотворення на полі П2.
Дві площини перпендикулярні, якщо одна з площин проходить через перпендикуляр до другої площини. Проведемо площину перпендикулярно до заданої, використовуючи розглянуту властивість, відповідно проведення перпендикуляра до площини. На рис. 41 площину задано горизонталлю h та фронталлю f. Через точку Адо цієї площини проведемо перпендикуляр n. Якщо через будь-яку точку прямої nпровести довільну пряму, то вона разом з перпендикуляром задає площину, перпендикулярну до заданої. Беручи до уваги, що пряму проводять довільно, їх може бути нескінченна множина.
Питання для самоконтролю
І. Як повинні бути розміщені дві мимобіжні прямі загального положення, щоб відстань між ними зображалась на одній з площин проекцій?
2. Чи може непрямий кут перетину двох прямих проектуватись на одній з площин проекцій прямим кутом?
3. Скільки площин можна провести через довільну точку простору перпендикулярно до даної прямої?
4. Скільки площин можна провести через довільну точку простору перпендикулярно до даної площини?
Перетворення комплексного креслення
Тема: Методи перетворення креслень. Заміна площин проекцій. Метод обертання. Плоско-паралельне переміщення.
Лекція – 4,5, 4 год.
Розв’язання більшості геометричних задач зводиться до визначення метричних та позиційних характеристик окремих фігур.
Фігура або геометричний елемент по відношенню до площин проекцій П1, П2 та П3 може займати загальне (незручне) і часткове (зручне) положення. При загальному положенні геометричних елементів і фігур розв’язок задач, як правило, більш складніший і розтягнутий по часу. Але від зміни розташування фігур відносно площин проекцій її характеристики не міняються. Тобто після перетворення комплексного креслення додаткові проекції дають можливість розв’язати задачі найпростішими графічними способами.
Основними методами перетворення креслень є:
- заміна площин проекцій;
- плоско-паралельне переміщення (обертання навколо невиявлених осей);
- обертання навколо проектуючих осей;
 |
- обертання навколо ліній рівня.
1 Заміна площин проекцій
На рис. 42 а в системі площин проекцій П1та П2показано точку А. Перпендикулярно до площини П1 проведено нову вертикальну площину П4, на яку ортогонально спроектовано точку А.
Таким чином, замість системи площин проекцій П1П2, з проекціями точки А1А2, одержано систему П1П4 з проекціями точки А1А4. При такій заміні відстань від старої проекції до старої осі дорівнює відстані від нової проекції до нової осі. На комплексному кресленні (рис. 42 б) цю відстань показано подвійною рискою.
Звідси можна зробити висновок про суть цього методу: розташування елементів або фігур залишається незмінним, а змінюється розташування площин проекцій. Нові площини вибираються завжди перпендикулярно до старих і так, щоб фігури проектувалися на них в частковому положенні.
Розглянемо чотири основні задачі перетворення креслень
а) перетворення прямої загального положення в пряму рівня (визначення натуральної величини відрізка прямої). На рис.43 зображено відрізок прямої загального положення АВ
 Щоб одержати його натуральну величину, тобто перетворити його в пряму рівня, досить провести нову площину паралельно одній з проекцій, на рисунку вісь х14 паралельна горизонтальній проекції прямої. Відклавши від нової осі відповідні відстані від фронтальних проекцій точок до старої осі, одержимо натуральну величину відрізка А4В4.
Щоб одержати його натуральну величину, тобто перетворити його в пряму рівня, досить провести нову площину паралельно одній з проекцій, на рисунку вісь х14 паралельна горизонтальній проекції прямої. Відклавши від нової осі відповідні відстані від фронтальних проекцій точок до старої осі, одержимо натуральну величину відрізка А4В4.
 |
б) перетворення прямої загального положення у проектуючу пряму. Для цього треба скористатись натуральною величиною відрізка, тобто виконати дії, описані в пункті а.
Якщо провести площину, перпендикулярну до натуральної величини (рис. 44), її слід вісь х45, то, відклавши відстань, позначену потрійною рискою, одержимо проекцію прямої у вигляді точки.
в) перетворення площини загального положення у проектуюче положення. Для цього в площині трикутника було проведено горизонталь А-1.Перпендикулярно до горизонтальної проекції горизонталі (рис.45 ) вибрано вертикальну площину (її горизонтальний слід – х14. При цьому горизонталь спроектувалася у точку А4=14, а весь відсік - в пряму С4А4В4. г) перетворення площини загального положення в площину рівня (визначення натуральної величини відсіку площини). Для цього треба скористатись проектуючим положенням площини, тобто виконати дії описані в пункті в). Паралельно прямій С4А4В<