Специальные функции формирования массивов
Если требуется сформировать матрицу, у которой элементы, расположенные по главной диагонали, равны единице, а остальные элементы равны нулю, можно воспользоваться функцией eye:
>> C=eye (3, 4)
C =
1 0 0 0
0 1 0 0
0 0 1 0
Чтобы заполнить матрицу случайными числами, можно обратиться к функциям rand и randn. Функция rand позволяет сформировать матрицу из случайных чисел, равномерно распределённых на интервале от 0 до 1:
>> C=rand (2, 3)
C =
0.2785 0.9575 0.1575
0.5469 0.9649 0.9706
Функция radn формирует матрицу из случайных чисел, распределённых по нормальному закону:
>> C=randn (2, 3)
C =
0.7254 0.7147 -0.1241
-0.0631 -0.2050 1.4897
Функция magic формирует так называемую «магическую матрицу», у которой сумма элементов каждого столбца, строки и диагонали равна одному и тому же числу. Эта функция имеет единственный аргумент, определяющий размер создаваемой квадратной матрицы (магический квадрат):
>> C=magic (3)
C =
8 1 6
3 5 7
4 9 2
Заметим, что простые преобразования (транспортирование, переворачивание строк и столбцов, поворот) сохраняют свойство матрицы быть кубическим квадратом.
С помощью функции pascal можно задать матрицу Паскаля (матрица Паскаля — это матрица, элементами которой являются биномиальные коэффициенты), структура которой соответствует треугольнику Паскаля:
>> C=pascal (3)
C =
1 1 1
1 2 3
1 3 6
Для отображения диагональных элементов матрицы служит функция diag. Так, например, для того, чтобы извлечь главную диагональ приведённой выше матрицы Паскаля, следует ввести команду
>> c=diag (C)
c =
Аналогичным образом можно извлечь, например, любую диагональ матрицы — для этого следует лишь указать её номер в качестве второго аргумента функции diag (при этом диагонали отсчитываются вверх и вниз от главной, которая по умолчанию имеет номер 0).
>> C=magic (3)
C =
8 1 6
3 5 7
4 9 2
>> c1=diag (C, 1)
c1 =
>> c2=diag (C, -1)
c2 =
Функция diag также позволяет сформировать такие матрицы, у которых элементы, расположенные по диагонали, соответствуют элементам некоторого вектора, а остальные элементы равны нулю. В качестве примера сформируем диагональную матрицу из вектор-строки a:
>> a=[4 1 -1]
a =
4 1 -1
>> D=diag (a)
D =
4 0 0
0 1 0
0 0 -1
Если элементами вектора требуется заполнить не главную диагональ, а какую-либо другую, следует указать её номер во втором аргументе функции diag:
>> D1=diag (a, 1)
D1 =
0 4 0 0
0 0 1 0
0 0 0 -1
0 0 0 0
>> D2=diag (a, -1)
D2 =
0 0 0 0
4 0 0 0
0 1 0 0
0 0 -1 0
ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦЫ
Пусть даны квадратная матрица А и ненулевой вектор-столбец х:
, 
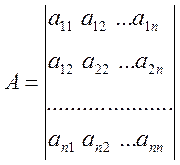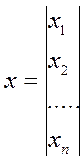
Умножив матрицу А на вектор-столбец х, получим вектор-столбец y
,
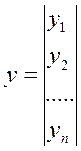т.е.
.
Если окажется, что координаты 
вектора yпропорциональны координатам 
данного вектора хс коэффициентом пропорциональности 
( 
), и, следовательно,
,
то ненулевой столбец х называется собственным вектором матрицы А, а коэффициент пропорциональности - собственным значением матрицы А.
Так как 
и 
, то 
.
Последнее соотношение можно переписать так:
,
где
, 
Соотношение 
представляет собой линейную, однородную систему уравнений, которая имеет ненулевые решения тогда и только тогда, когда ее определитель равен нулю
,
или в развернутом виде
Если раскрыть этот определитель, то получим многочлен n-ой степени относительно , решая это уравнение, найдем n собственных значений .
Ручной счет.
Будем определять одно собственное значение методом итераций.
В качестве начального приближения возьмем
Нулевой шаг
, 
,
1-й шаг
, 
,
2-й шаг
, 
,
n-й шаг
, 
,
Оценка погрешности: 
Пример
Ручной счет
Начальное приближение: 
0-й шаг
, 
, 
1-й шаг
, 
,
2-й шаг
,
,
3-й шаг
,
Оценка погрешности: 
Ответ:
, 
Лабораторная работа 3.
Вычисление собственных значений и собственных векторов
симметричной матрицы
Задание.
Вычислить собственные значения и собственные векторы симметричной матрицы на ЭВМ (требуется составить программу в системе MATLAB (на M-языке)) и определить максимальное по модулю собственное число и соответствующий ему собственный вектор степенным методом
Варианты задания.
где K– номер факультета (института); G –
номер группы; S – номер студента по журналу.
Выполнение работы на ЭВМ.
Для выполнения создается М-файл. Ниже приведен текст М-файла.
A=input('Введите матрицу A=');
A=A/6;
n=size(A);
fprintf('\n Исходная матрица (Матрица A) \n');
for i=1:n
fprintf('%6.2f',A(i,:));
fprintf('\n');
end
[T,J]=eig(A);
x=diag(J);
fprintf('\n Вектор собственных чисел \n');
fprintf('%6.2f \n',x);
fprintf('\n Матрица собственных векторов \n');
for i=1:n
fprintf('%12.4g',T(i,:));
fprintf('\n');
end
Результаты расчета в командном окне:
Исходная матрица (Матрица A)
5.00 -3.00 4.00
-3.00 12.00 -3.00
4.00 -3.00 5.00
Вектор собственных чисел
1.00
6.00
15.00
Матрица собственных векторов
0.7071 0.5774 0.4082
0 0.5774 -0.8165
-0.7071 0.5774 0.4082
Ниже приведены пояснения к приведенному тексту программы.
1. Заметим, что в представленной программе (а также в последующих программах, относящихся к данной лабораторной работе), при задании значений элементов матрицы множитель 1/6 учитывать не надо – деление на 6 уже предусмотрено в тексте программы. Это сделано для упрощения ввода исходных данных и исключения соответствующих погрешностей.
После запуска программы в ответ на запрос о вводе матрицы A следует задать: [30 -18 24; -18 72 -18; 24 -18 30].
2. Функция [V,D]=eig(A) в системе MATLAB возвращает матрицу
собственных векторов V (собственные векторы расположены по столбцам) и диагональную матрицу D собственных значений (матрица Жордана (элементы, расположенные на ее главной диагонали есть собственные значения матрицы A); каноническая форма матрицы A), т.е., по сути, определяется разложение Жордана (но при условия отсутствия в матрице Жордана жордановых клеток порядка, большего единицы) и справедливо равенство A*V=V*D. В частном случае, при обращении типа d=eig(A) возвращается
вектор d, координаты (элементы) которого есть собственные значения (собственные числа) матрицы A.