Метод поділу відрізка навпіл
ЛАБОРАТОРНА РОБОТА №8
Тема: Уточнення коренів методом поділу навпіл (половинного ділення, бісекції, дихотомії).
Мета роботи: навчитися розв’язувати рівняння з однією змінною, використовуючи обчислюванні методи, навчитися відокремлювати корені, уточнювати їх за допомогою метода поділу навпіл (дихотомії).
Запитання для самоконтролю
1. У чому полягає геометричний сенс методу половинного ділення?
2. Чи завжди дозволяє метод половинного ділення обчислити відокремлений корінь рівняння з заданою похибкою?
3. Як вибираються кінці відрізка наступного інтервалу в методі половинного ділення?
4. Якими властивостями повинна володіти функція f (х), щоб методом половинного ділення гарантовано вирішити рівняння f (х) = 0?
5. Що необхідно для знаходження методом половинного ділення хоча б одного дійсного кореня рівняння: f (x) = 0?
6. Чи можна знайти корінь методом половинного ділення, якщо він знаходиться на межі інтервалу?
Теоретичні відомості.
Метод поділу відрізка навпіл
Метод поділу відрізка пополам (або метод дихотомії) застосовний для уточнення кореня рівняння f(x)=0 з наперед заданою точністю.
Нехай на проміжку [а; b]функція f(x) неперервна і набуває на кінцях проміжку значень різних знаків, тобто f (а) • f (b) < 0. Це означає, що на [а; b] рівняння f(x)=0 має принаймні один корінь. Цей корінь можна визначити з наперед заданою точністю методом поділу відрізка пополам.
Суть методу полягає в тому, що відрізок, на якому міститься корінь, поступово звужують, зменшуючи його щоразу вдвоє, поки не досягнуть потрібної точності визначення кореня.
Позначимо лівий кінець відрізка, на якому міститься корінь, буквою u0 (а=u0), правий – буквою v0 (b=v0) і знайдемо середину цього відрізка: с =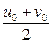 
.Оскільки (за умовою) f(u0)f(v0)<0, то f(a)f(с)>0, або f(с)f(в)<0, або f(с) = 0. Якщо f(с)= 0, то корінь х* = с (Рис. 1).
Зрозуміло, що у випадку f(a)f(с)>0 корінь міститься на відрізку [c; v0]. У випадку f(а)f(c) < 0 корінь міститься на відрізку [u0; c].
Якщо довжина відрізка, на якому міститься корінь, не перевищує заданої величини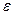 
, то це означає, що х* знайдено з точністю до 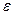, бо
|с-х*| 
с-u0.
Якщо заданої точності ще не досягнуто, то, позначивши с через u0 у випадку f(a)f(с)>0 або через v0 у випадку f(а)f(с)<0, знову знаходимо середину відрізку [u0; v0] і повторюємо обчислення.
|
Переконатися в тому, що потрібна точність при обчисленні кореня х* уже досягнута, можна й іншим способом. Якщо на деякому відрізку [а; b] функція f(х) диференційована і 0‹m |f’(x)| (у цьому випадку на [а; b] міститься єдиний корінь рівняння f(х)=0) і якщо 
, (1)
то можна вважати, що х – наближене значення кореня х* з точністю до .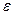
Дійсно, за теоремою про середнє маємо:
|f(x)-f(х*)|=|(x- х*) 
| (x‹ 
‹ х*, або х*‹ ‹ х).
Враховуючи, що f(х*)=0, дістанемо:
|x-х*|= 
, де m 
.
Умову (1) можна використати для перевірки близькості х до х*, якщо х знайдено будь-яким способом, а не тільки методом ділення відрізку пополам.
Зауважимо, що близькість до нуля f(х) не означає близькості х до х* (Рис.2).
Послідовність наближень, знайдених методом поділу проміжку пополам, збігається до кореня х* рівняння f(х)=0, причому щоразу маємо для х* оцінки знизу і зверху: и0 ≤ х*≤ v0.
При обчисленні значень f(х) достатньо мати одну-дві правильні значущі цифри, оскільки нас цікавить лише знак f(х) при даному х.