Распределение Бозе–Эйнштейна

Большое каноническое распределение квантовой системы

 

Многоуровневая квантовая система в виде идеального газа при фиксированных T, V, N описывается каноническим распределением. Система с 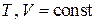, обменивающаяся энергией и частицами с термостатом, описывается большим каноническим распределением. Получим это распределение для квантовой системы. Далее найдем распределение частиц по уровням в многоуровневой системе.

Состояние i многоуровневой системы. Ограниченная в пространстве стационарная квантовая система имеет дискретный спектр энергии

 

,

 

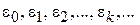определяемый плотностью состояний. Частное распределение частиц по уровням энергии образует состояние системы

 

,

 

где – число частиц на уровне . Полная энергия и число частиц в состоянии i

,

 

. (4.1)

 

Вероятность состояния i. Используем большое каноническое распределение для классической системы

 

.

 

Распределение для квантовой системы имеет аналогичный вид согласно принципу соответствия. Для вероятности дискретного состояния i с числом частиц и энергией получаем

 

, (4.2)

 

где – химический потенциал равновесной системы. Подставляем (4.1) в (4.2)

. (4.2а)

 

Распределения частиц по уровням энергии. Статистически независимые уровни энергии рассматриваем как подсистемы. По теореме умножения вероятностей независимых событий вероятность состояния системы равно произведению вероятностей состояний ее независимых подсистем

,

где – вероятность нахождения частиц на уровне k. Сравниваем с (4.2а) и получаем

, (4.3)

 

. (4.4)

Учтено, что для равновесной системы химический потенциал одинаков для всех подсистем.

Статистическая сумма подсистемы с энергией находится из условия нормировки

.

Подстановка (4.3) дает

. (4.5)

 

Для системы в макроскопическом объеме спектр энергии квазинепрерывный . В (4.3) и (4.5) заменяем и получаем вероятность нахождения n частиц в состоянии с энергией и статистическую сумму

 

,

 

. (4.5а)

 

Среднее число частиц в состоянии с энергией без учета вырождения по спину, которое учитывается плотностью состояний, находим из определения среднего и (4.5а)

 

. (4.6)

 

Результат выражается через статистическую сумму (4.5а)

 

. (4.7)

 

Формула (4.7) совпадает с формулой классической теории, подтверждая правило соответствия.

 

Распределение Ферми–Дирака

Среднее число фермионов в одном состоянии. По принципу Паули в одном состоянии может быть не более одного фермиона, тогда

.

Из (4.5а) и (4.6) находим

,

 

.

 

Получаем распределение Ферми–Дирака

 

(4.8)

 

– среднее число фермионов в состоянии с энергией e. Поскольку , то – степень заполнения состояния. Химический потенциал , где – концентрация фермионов; m – масса частицы; s – спин фермиона.

Функция распределения. При учитываем

 

,

 

 

тогда

. (4.8а)

 

Распределение фермионов по энергии при

 

Согласно принципу Паули, на одном уровне энергии может быть не более двух электронов с противоположными проекциями спина. Попав в систему, электрон стремится занять свободное место с наименьшей энергией. Согласно (4.8а), при уровни с энергией заполнены полностью, уровни свободные. При добавлении электрона в систему, он занимает свободное состояние вблизи уровня , энергия системы увеличивается на . Следовательно, возрастает с ростом концентрации электронов. Химический потенциал равен средней энергии частицы, добавляемой в систему. В результате химический потенциал фермионного газа при равен энергии самого высокого заполненного уровня.

Наибольшая энергия электрона при называется энергией Ферми eF, соответствующий уровень – уровнем Ферми, в результате

 

.

 

При любой температуре согласно (4.8)

 

выполняется

. (4.8б)

 

Химический потенциал равновесного газа фермионов равен энергии состояния со степенью заполнения 1/2. При тепловое движение перебрасывает частицы через уровень Ферми, и они занимают уровни с большей энергией, освобождая уровни с меньшей энергией. Прямоугольный график распределения сглаживается.

Плотность состояний увеличивается с ростом энергии, например, для трехмерного газа электронов . Поэтому ширина полосы энергии ниже , которую освобождают электроны, перебрасываемые тепловым движением, больше ширины полосы, которую они занимают выше . В результате средняя энергия перебрасываемых электронов, то есть химический потенциал, с увеличением температуры медленно уменьшается.

 

 

Для оценки переходной области вблизи μ вычисляем производную распределения по энергии при . Из (4.8)

 

получаем

.

При

.

 

Ширина переходной области увеличивается с ростом температуры. При ширина переходной области стремится к нулю, и функция становится прямоугольной.

 

Распределение Бозе–Эйнштейна

Среднее число бозонов в одном состоянии. Для бозонов допустимо любое число частиц в одном состоянии

 

.

Из (4.5а)

получаем

.

 

Сумма является геометрической прогрессией. Она сходится, если основание прогрессии , тогда . Учитывая , получаем, что химический потенциал бозонов не может быть положительным

 

. (4.9)

 

Суммируем геометрическую прогрессию

 

,

 

получаем статистическую сумму

,

 

.

Подставляем в (4.7)

,

находим

.

 

Получаем распределение Бозе–Эйнштейна

 

(4.10)

 

– среднее число бозонов в состоянии с энергией e. Условие

 

 

обеспечивает при любой энергии и температуре. С ростом температуры химический потенциал бозонов медленно уменьшается, а его модуль увеличивается. При находим

 

. (4.11)

 

Чем больше , тем меньше B. В нефизической области при из (4.10) получаем .