Построение математической модели (на контрольном примере)

Как уже была сказано во введении, и в экономике и в технике имеется большое количество задач, при решении которых специалисты должны принимать оптимальные решения. Можно напомнить, что за разработку метода оптимального распределения ресурсов академик Л.В. Конторович в 1974 г. был удостоен Нобелевской премии по экономике.

Решение любой оптимизационной задачи начинается с построения её математической модели, представляющей собой совокупность алгебраических уравнений.

В данных методических указаниях поиск оптимального решения рассматривается на примере установления плана выпуска продукции в заданном ассортименте, исходя из наилучшего использования производственных ресурсов и обеспечения максимальной экономической эффективности производства.

Предположим, что предприятие может выпускать продукцию четырех видов Прод1-Прод4 (n=4). Для их изготовления требуются ресурсы трех видов (m=3), например, трудовые ресурсы, сырьё и финансы. Известно количество ресурса каждого вида, необходимое для выпуска единицы продукции каждого вида, т.н. нормы расхода ресурсов. Кроме того, известны ограниченные объёмы этих ресурсов на планируемый период, т.н. запасы ресурсов. Известна прибыль, получаемая от реализации единицы продукции каждого вида - единичная прибыль. Заданы также граничные значения объёмов выпуска каждого вида продукции (верхняя или/и нижняя границы) и соотношения в выпуске отдельных видов продукции. Требуется определить оптимальное количество выпуска каждого вида продукции, при котором будут получена максимальная прибыль.

Для построения математической модели задачи введем следующие обозначения:

x_j - количество выпускаемой продукции j-го типа, j = 1, n;

b_i - количество располагаемых ресурсов i-го вида, i = 1,m;

a_ij - норма расхода ресурса i-го вида для выпуска единицы продукции j-го типа;

g_i - ограничение на количество располагаемых ресурсов i-го вида;

k_j - нижняя граница объёма производства продукции j-го типа;

v_j - верхняя граница объёма производства продукции j-го типа.

Тогда математическая модель может быть представлена в виде набора следующих уравнений (1.2.1):

(1.2.1)

Как уже указывалось, в связи с тем, что и целевая функция и ограничения имеют линейный характер, данная задача относятся к задачамлинейного программирования.

В линейном программировании фундаментальное значение имеет теория двойственности. Именно на основе этой теории выполняется анализ полученных оптимальных решений.

Рассмотрим кратко основные положения этой теории.

Каждой задаче линейного программирования, которую будем называть исходной, соответствует двойственная задача, которая формулируется по следующим правилам.

1. Каждому i-му ограничению исходной задачи соответствует переменная двойственной задачи, которую называют двойственной переменной.

2. Каждой переменной исходной задачи соответствует ограничение двойственной задачи.

3. Матрица коэффициентов при двойственных переменных в ограничениях двойственной задачи является транспонированной матрицей коэффициентов при переменных в ограничениях исходной задачи (строки одной матрицы являются соответствующими столбцами другой).

4. Если в исходной задаче ограничения имеют знаки неравенства ³, то в двойственной они будут £.

5. Правые части ограничений в двойственной задаче равны коэффициентам при переменных в целевой функции и исходной задачи.

6. Коэффициенты при двойственных переменных в целевой функции двойственной задачи равны правым частям ограничений исходной задачи.

7. Максимизация целевой функции исходной задачи заменяется минимизацией целевой функции двойственной задачи.

Таким образом, исходной задаче в общем виде:

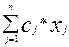F = ® max

£ b_i (1.2.2)

x_j ³ 0

соответствует двойственная:

F_д = ® min

(1.2.3)

В соответствии с правилом п.7 –

maxF = minF_д, а т.к. minF_д =

Тогда последнюю формулу для наглядности можно записать так:

maxF = (1.2.4)

Из (1.2.4) видно, что двойственная переменная z_i является коэффициентом при b_i и, следовательно, показывает, как изменится целевая функция при изменении ресурса b_i на единицу.

В литературе по оптимизации двойственные переменные z_i принято называть двойственными оценками. В отчетах Excel двойственная оценка называется теневой ценой.

Пояснить значение двойственных оценок можно следующим образом.

Если некоторый i-й ресурс используется не полностью, т.е. имеется его некоторый резерв, значит, дополнительная переменная в ограничении для данного ресурса будет больше нуля, а двойственная оценка этого ограничения равна нулю. Следовательно, уменьшение этого ресурса на величину резерва не влияет на оптимальное решение. Увеличение этого ресурса вызовет только увеличение резерва, также без изменения результата решения.

Если же какой то ресурс используется полностью, то его увеличение или уменьшение повлияет на величину целевой функции, а значение двойственной оценки показывает, на сколько изменится целевая функция при изменении этого ресурса на одну единицу.

Значения двойственных переменных специально вычислять не надо, они определяются автоматически в процессе поиска оптимального решения.

• ⇐ Назад
• 123
• 4
• 5
• 6
• Далее ⇒