Базис и размерность линейного пространства. Признак линейной зависимости и независимости векторов в координатной форме.

Линейное пространство. Разложение вектора по базису.

Рассмотрим непустое множество 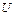элементов 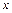, , , … и — множество всех вещественных чисел. Линейным векторным пространством называется множество 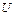, в котором определены две линейные операции:

1. Сложение элементов множества, т.е. если , , то .

2. Умножение элементов множества 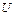на произвольные числа , т.е. если , , то , причем эти операции удовлетворяют следующим аксиомам:

1. (коммутативность);

2. (ассоциативность);

3. Существует элемент , такой, что ;

4. Для существует противоположный вектор , такой, что ;

5. ;

6. Для выполняется равенство , ;

7. Для и справедливо равенство ;

8. Для и .

Линейная зависимость и независимость векторов

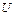Если , , …, — векторы пространства , а , , …, — произвольные числа из , то выражение называется линейной комбинацией векторов , , …, , а числа , , …, — коэффициентами этой комбинации.

Линейная комбинация называется тривиальной, если все ее коэффициенты равны нулю ( ).

Система векторов называется линейно зависимой, если существует равная нулю нетривиальная комбинация этих векторов (не все ). В противоположном случае (т.е. в случае равенства нулю только тривиальной линейной комбинации) система называется линейно независимой.

Теорема. Для того, чтобы система векторов , , …, была линейно зависимой необходимо и достаточно, чтобы один из них был линейной комбинацией остальных векторов. Система, содержащая нулевой вектор, линейно зависима.

Базис и размерность линейного пространства. Признак линейной зависимости и независимости векторов в координатной форме.

Любая совокупность векторов линейного пространства называется базисом этого пространства, если выполняются следующие условия:

1. Все векторы данной совокупности линейно независимы;

2. Любой вектор пространства является линейной комбинацией векторов данного пространства.

Максимальное число линейно независимых векторов этого пространства называется размерностью векторного пространства (размерность пространства совпадает с числом его базисных векторов).

Базисные векторы принято обозначать , , …, .

Тогда любой вектор 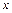этого пространства линейно выражается через базисные:

;

, , …, — координаты вектора в базисе , , …, .

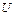Пусть имеется система векторов , , …, пространства с выбранным базисом , , …, , тогда

. (1)

Рассмотрим линейную комбинацию векторов ( )

(2)

С учетом координатного представления векторов, последнее равенство перепишется в виде:

, .

Матрица этой системы

.

Координаты вектора расположены в -ом столбце. Отсюда следует, что векторы , …, линейно зависимы тогда и только тогда, когда система (2) имеет ненулевое решение (то есть определитель матрицы этой системы в случае должен быть равен нулю).

Иначе, для существования линейной зависимости между векторами необходимо и достаточно существование такой же зависимости между столбцами из координат этих векторов.

Векторы линейно независимы тогда и только тогда, когда ранг матрицы равен числу векторов этой системы.

 

 

Упражнения.

№ 1. Указать, какие из нижеперечисленных множеств образуют линейное векторное пространство (устно).

а) Совокупность векторов плоскости, концы которых лежат в первой четверти (предполагается, что векторы откладываются от начала координат)

/Нет, т.к. отсутствует противоположный элемент/

б) Совокупность векторов плоскости не параллельных некоторой оси.

/Нет, т.к. при сложении может получиться вектор, параллельный этой оси/

в) Множество квадратных матриц -го порядка. /Да/.

г) Множество невырожденных квадратных матриц. /Нет/

д) Множество всех вещественных функций, непрерывных на . (Пространство ). /Да/

№ 2. Что означает условие линейной зависимости векторов некоторой плоскости?

коллинеарность векторов, в координатной форме .

№ 3. Что означает условие линейной зависимости в трехмерном пространстве?

, т.е. векторы лежат в одной плоскости (компланарность) в координатной форме

.

№ 4. Будут ли линейно зависимы следующие системы векторов обычного трехмерного пространства

а) и . Да.

б) и . Нет.

и равен числу векторов и .

в) , ,

. Нет.

№ 5. Пусть — пространство квадратных матриц второго порядка. Показать, что векторы

, , ,

линейно независимы и образуют базис данного пространства.

Решение.

Покажем, что только при .

.

Матрица будет нулевой, когда все ее элементы равны 0, т.е. векторы линейно независимы и любая матрица вида есть линейная комбинация , , , .

Устно. Какова размерность данного пространства? ( )

Какова размерность пространства квадратных матриц третьего порядка? ( ).

№ 6. Показать, что векторы , , образуют базис трехмерного пространства. Найти координаты вектора в этом базисе , , , .

Решение.

1) Покажем, что , , линейно независимы. В данном случае имеет вид

оно равносильно системе

.

Если , то система имеет только нулевое решение.

.

и равен числу векторов они линейно независимы.

2) Требуется найти числа такие, что или в координатной форме:

или

.

Решение найдем методом Гаусса

, , .

Ответ: , т.е. векторы в разных базисах имеют разные координаты.