Особенности контроля в спортивной тренировке
Среди актуальных проблем физического воспитания значительное место занимает такая специфическая проблема, как развитие основных физических (двигательных) качеств. Важную роль здесь играют не только пути их развития и совершенствования, но и средства их контроля, особенно педагогического.
Задача последнего состоит в необходимости ознакомиться с вопросами, решаемыми с помощью педагогических наблюдений, познакомиться с методами и организацией их проведения. Такие наблюдения могут проводиться не только во время занятий или тренировки, но и до и после них.
Основная задача этих наблюдений - совершенствование учебно-тренировочного процесса с целью получения наилучшего эффекта. Такая задача может быть решена плодотворно с участием врача, хорошо знающего спорт, методы планирования, а педагог-тренер, в свою очередь, должен обладать необходимыми медицинскими знаниями. При этом тренер должен четко представлять какие сведения он может получить с помощью врача и какие самостоятельно. Такие наблюдения в естественных условиях спортивной деятельности, проводимые совместно с врачом позволяют оценить физическую подготовленность и специальную тренированность спортсмена, оценить правильность используемых методик и режима тренировок, предупредить перенапряжения, переутомление и перетренерованность. Исходя их вышеизложенного, эти наблюдения следует называть врачебно-педагогическими.
Важнейшей задачей врачебно-педагогического контроля является уточнения в планировании учебно-тренировочного процесса, дозировка физических нагрузок в недельном цикле, определения длительности интервалов отдыха между упражнениями и тренировками, нахождение наиболее рационального сочетания различных средств тренировок и т.п.
Практическая реализация врачебно-педагогического контроля осуществляется в системе специально реализуемых проверок, включаемых в содержание занятий по физическому воспитанию, либо тренировочных занятий.
Такие проверки позволяют вести систематический учет по двум наиболее важным направлениям:
§ определение степени усвоения техники двигательных действий;
§ определение уровня развития двигательных (физических) качеств.
Существующие методы врачебно-педагогического контроля можно разделить на две группы:
§ не тренирующие сложной аппаратуры, отличающиеся простотой методики оценки (визуальное наблюдение, определение частоты дыхания, измерение артериального давления, веса тела, различные координационные пробы и др.)
§ требующие довольно сложной аппаратуры и специально подготовленных людей, проводящих контроль (Электрокардиография и др.)
В системе педагогического контроля за усвоением техники двигательных действий, осуществляемого в процессе занятий преподавателями физического воспитания, принято различать три вида проверок (контроля):
§ предварительную (прием первичных контрольных нормативов);
§ текущую (отмечается преподавателем-тренером в журнале или дневнике);
§ итоговую (прием государственных тестов).
Особое место при проведении педагогического контроля занимает медицинское обеспечение - одно из решающих условий рационального использования средств физической культуры и спорта, высокой эффективности проведения учебно-тренировочных занятий.
Медицинское обеспечение способствует реализации принципа оздоровительной направленности системы физического воспитания и осуществляется в виде врачебного контроля.
6. Шкала наименований (номинальная шкала)
Это самая простая из всех шкал. В ней числа выполняют роль ярлыков и служат для обнаружения и различения изучаемых объектов (например, нумерация игроков футбольной команды). Числа, составляющие шкалу наименований, разрешается менять местами. В этой шкале нет отношений типа "больше — меньше", поэтому некоторые полагают, что применение шкалы наименований не стоит считать измерением. При использовании шкалы наименований могут проводится только некоторые математические операции. Например, ее числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.
Шкала порядка
Есть виды спорта, где результат спортсмена определяется только местом, занятым на соревнованиях (например, единоборства). После таких соревнований ясно, кто из спортсменов сильнее, а кто слабее. Но насколько сильнее или слабее, сказать нельзя. Если три спортсмена заняли соответственно первое, второе и третье места, то каковы их различия в спортивном мастерстве, остается неясным: второй спортсмен может быть почти равен первому, а может быть существенно слабее его и быть почти одинаковым с третьим. Места, занимаемые в шкале порядка, называются рангами, а сама шкала называется ранговой или неметрической. В такой шкале составляющие ее числа упорядочены по рангам (т.е. занимаемым местам), но интервалы между ними точно измерить нельзя. В отличие от шкалы наименований шкала порядка позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства в виде суждений: "больше — меньше", "лучше — хуже" и т.п.
С помощью шкал порядка можно измерять качественные, не имеющие строгой количественной меры, показатели. Особенно широко эти шкалы используются в гуманитарных науках: педагогике, психологии, социологии. К рангам шкалы порядка можно применять большее число математических операций, чем к числам шкалы наименований.
Шкала интервалов
Это такая шкала, в которой числа не только упорядочены по рангам, но и разделены определенными интервалами. Особенность, отличающая ее от описываемой дальше шкалы отношений, состоит в том, что нулевая точка выбирается произвольно. Примерами могут быть календарное время (начало летоисчисления в разных календарях устанавливалось по случайным причинам), суставной угол (угол в локтевом суставе при полном разгибании предплечья может приниматься равным либо нулю, либо 180о), температура, потенциальная энергия поднятого груза, потенциал электрического поля и др.
Результаты измерений по шкале интервалов можно обрабатывать всеми математическими методами, кроме вычисления отношений. Данные шкалы интервалов дают ответ на вопрос "на сколько больше?", но не позволяют утверждать, что одно значение измеренной величины во столько-то раз больше или меньше другого. Например, если температура повысилась с 10о до 20о по Цельсию, то нельзя сказать, что стало в два раза теплее.
Шкала отношений
Эта шкала отличается от шкалы интервалов только тем, что в ней строго определено положение нулевой точки. Благодаря этому шкала отношений не накладывает никаких ограничений на математический аппарат, используемый для обработки результатов наблюдений.
В спорте по шкале отношений измеряют расстояние, силу, скорость и десятки других переменных. По шкале отношений измеряют и те величины, которые образуются как разности чисел, отсчитанных по шкале интервалов. Так, календарное время отсчитывается по шкале интервалов, а интервалы времени — по шкале отношений.
При использовании шкалы отношений (и только в этом случае!) измерение какой-либо величины сводится к экспериментальному определению отношения этой величины к другой подобной, принятой за единицу. Измеряя длину прыжка, мы узнаем во сколько раз эта длина больше длины другого тела, принятого за единицу длины (метровой линейки в частном случае); взвешивая штангу, определяем отношение ее массы к массе другого тела — единичной гири "килограмма" и т.п. Если ограничиться только применением шкал отношений, то можно дать другое (более узкое, частное) определение измерению: измерить какую-либо величину — значит найти опытным путем ее отношение к соответствующей единице измерения.
В таблице 3 приведены сводные сведения о шкалах измерения.
7. Теоретические сведения
Измерением (в широком смысле слова) называют установление соответствия между изучаемыми явлениями, с одной стороны, и числами, с другой.
Чтобы результаты разных измерений можно было сравнивать друг с другом, они должны быть выражены в одних и тех же единицах. В 1960 г. на Международной генеральной конференции по мерам и весам была принята Международная система единиц, получившая сокращенное название СИ.
СИ в настоящее время включает семь независимых друг от друга основных единиц, из которых в качестве производных выводят единицы остальных физических величин. Производные единицы определяются на основе формул, связывающих между собой физические величины.
Например, единица длины (метр) и единица времени (секунда) — основные единицы, а единица скорости (метр за секунду [м/с]) — производная. Совокупность выбранных основных и образованных с их помощью производных единиц для одной или нескольких областей измерения называется системой единиц (табл. 1).
Таблица 1
Основные единицы СИ
| Единица |
| Величина | Размерность | Название | Обозначение |
| русское | международное | |||
| Длина | L | Метр | м | m |
| Масса | M | Килограмм | кг | kg |
| Время | T | Секунда | с | S |
| Сила эл. тока | I | Ампер | А | A |
| Температура | q | Кельвин | К | K |
| Кол-во вещ-ва | N | Моль | моль | mol |
| Сила света | G | Канделла | Кд | cd |
Размерностью называется выражение, связывающее производную величину с основными величинами системы при коэффициенте пропорциональности, равном единице. Например, размерность скорости равна  , а размерность ускорения равна
, а размерность ускорения равна 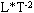
Никакое измерение не может быть выполнено абсолютно точно. Результат измерения неизбежно содержит погрешность, величина которой тем меньше, чем точнее метод измерения и измерительный прибор.
Основная погрешность — это погрешность метода измерения или измерительного прибора, которая имеет место в нормальных условиях их применения.
Дополнительная погрешность — это погрешность измерительного прибора, вызванная отклонением условий его работы от нормальных.
Величина D А=А-А0, равная разности между показанием измерительного прибора (А) и истинным значением измеряемой величины (А0), называется абсолютной погрешностью измерения. Она измеряется в тех же единицах, что и сама измеряемая величина.
Относительная погрешность — это отношение абсолютной погрешности к значению измеряемой величины:
В тех случаях, когда оценивается не погрешность измерения, а погрешность измерительного прибора, за максимальное значение измеряемой величины принимают предельное значение шкалы прибора. В таком понимании наибольшее допустимое значение D Па, выраженное в процентах, определяет в нормальных условиях работы класс точности измерительного прибора.
Систематической называется погрешность, величина которой не меняется от измерения к измерению. В силу этой своей особенности систематическая погрешность часто может быть предсказана заранее или в крайнем случае обнаружена и устранена по окончании процесса измерения.
Тарированием (от нем. tarieren) называется проверка показаний измерительных приборов путем сравнения с показаниями образцовых значений мер (эталонов* ) во всем диапазоне возможных значений измеряемой величины.
Калибровкой называется определение погрешностей или поправка для совокупности мер (например, набора динамометров). И при тарировании, и при калибровке к входу измерительной системы вместо спортсмена подключается источник эталонного сигнала известной величины. Например, тарируя установку для измерения усилий, на тензометрической платформе поочередно помещают грузы весом 10, 20, 30 и т.д. килограммов.
Рандомизацией (от англ. random — случайный) называется превращение систематической погрешности в случайную. Этот прием направлен на устранение неизвестных систематических погрешностей. По методу рандомизации измерение изучаемой величины производится несколько раз. При этом измерения организуют так, чтобы постоянный фактор, влияющий на их результат, действовал в каждом случае по-разному. Скажем, при исследовании физической работоспособности можно рекомендовать измерять ее многократно, всякий раз меняя способ задания нагрузки. По окончании всех измерений их результаты усредняются по правилам математической статистики.
Случайные погрешности возникают под действием разнообразных факторов, которые ни предсказать заранее, ни точно учесть не удается.
Стандарт — нормативно-технический документ, устанавливающий комплекс норм, правил, требований к объекту стандартизации и утвержденный компетентным органом — Государственным комитетом по стандартизации. В спортивной метрологии объектом стандартизации являются спортивные измерения.
8. Точность измерения. Основное понятие. Критерии выбора точности измерений. Классы точности средств измерений. Примеры средств измерений разных классов точности.
Измерение – совокупность операций по применению технического средства, хранящего единицу величины, обеспечивающих нахождение соотношения измеряемой величины с ее единицей в явном или неявном виде и получение значения этой величины.
Вообще метрология – это наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Усовершенствование точности измерений стимулировало развитие наук, предоставляя более достоверные и чувствительные средства исследований.
От точности средств измерения зависит эффективность выполнения различных функций: погрешности счетчиков энергии приводят к неопределенности в учете электроэнергии; погрешности весов ведут к обману покупателей или к большим объемам неучтенного товара.
Повышение точности измерений позволяет определить недостатки технологических процессов и устранить эти недостатки, что приводит к повышению качества продукции, экономии энергетических и тепловых ресурсов, сырья, материалов.
Измерения могут быть классифицированы по характеристике точности на:
- Равноточные – ряд измерений какой-либо величины, выполненных одинаковыми
по точности средствами измерений и в одних и тех же условиях;
- Неравноточные - ряд измерений какой-либо величины, выполненных
несколькими различными по точности СИ и (или) в нескольких разных
условиях.
К разным видам средств измерения предъявляют специфические требования:
например, лабораторные средства должны обладать повышенной точностью и
чувствительностью. Высокоточными СИ являются, например, эталоны.
Эталон единицы величины – средство измерений, предназначенное для
воспроизведения и хранения единицы величины, кратных или дольных ее
значений с целью передачи ее размера другим средствам измерений данной
величины. Эталоны являются высокоточными средствами измерений и поэтому
используются для проведения метрологических измерений в качестве средств
передачи информации о размере единицы. Размер единицы передается «сверху
вниз» от более точных средств измерений к менее точным «по цепочке»:
первичный эталон ( вторичный эталон ( рабочий эталон 0-го разряда ( рабочий
эталон 1-го разряда … ( рабочее средство измерений.
Метрологические свойства средств измерений – это свойства, влияющие на
результат измерений и его погрешность. Показатели метрологических свойств
являются их количественной характеристикой и называются метрологическими
характеристиками. Все метрологические свойства средств измерений можно
разделить на две группы:
. Свойства, определяющие область применения СИ
. Свойства, определяющие качество измерения. К таким свойствам относятся
точность, сходимость и воспроизводимость.
Наиболее широко в метрологической практике используется свойство точности
измерений, которое определяется погрешностью.
Погрешность измерения – разность между результатом измерения и истинным
значением измеряемой величины.
Точность измерений СИ – качество измерений, отражающее близость их
результатов к действительному (истинному) значению измеряемой величины.
Точность определяется показателями абсолютной и относительной погрешности.
Абсолютная погрешность определяется по формуле: Хп= Хп - Х0,
где: Хп – погрешность поверяемого СИ; Хп – значение той же самой
величины, найденное с помощью поверяемого СИ; Х0 - значение СИ, принятое за
базу для сравнения, т.е. действительное значение.
Однако в большей степени точность средств измерений характеризует
относительная погрешность, т.е. выраженное в процентах отношение абсолютной
погрешности к действительному значению величины, измеряемой или
воспроизводимой данным СИ.
В стандартах нормируют характеристики точности, связанные и с другими
погрешностями:
Систематическая погрешность – составляющая погрешности результата
измерения, остающаяся постоянной или закономерно изменяющейся при повторных
измерениях одной и той же величины. Такая погрешность может проявиться,
если смещен центр тяжести СИ или СИ установлен не на горизонтальной
поверхности.
Случайная погрешность – составляющая погрешности результата измерения,
изменяющаяся случайным образом в серии повторных измерений одного и того же
размера величины с одинаковой тщательностью. Такие погрешности не
закономерны, но неизбежны и присутствуют в результатах измерения.
Погрешность измерений не должна превышать установленных пределов,
которые указаны в технической документации к прибору или в стандартах на
методы контроля (испытаний, измерений, анализа).
Чтобы исключить значительные погрешности, проводят регулярную поверку
средств измерений, которая включает в себя совокупность операций,
выполняемых органами государственной метрологической службы или другими
уполномоченными органами с целью определения и подтверждения соответствия
средства измерений установленным техническим требованиям.
В повседневной производственной практике широко пользуются обобщенной
характеристикой – классом точности.
Класс точности средств измерений – обобщенная характеристика,
выражаемая пределами допускаемых погрешностей, а также другими
характеристиками, влияющими на точность. Классы точности конкретного типа
СИ устанавливают в нормативных документах. При этом для каждого класса
точности устанавливают конкретные требования к метрологическим
характеристикам, в совокупности отражающим уровень точности СИ данного
класса. Класс точности позволяет судить о том, в каких пределах находится
погрешность измерений этого класса. Это важно знать при выборе СИ в
зависимости от заданной точности измерений.
Обозначение классов точности осуществляются следующим образом:
. Если пределы допускаемой основной погрешности выражены в форме
абсолютной погрешности СИ, то класс точности обозначается прописными
буквами римского алфавита. Классам точности, которым соответствуют
меньшие пределы допускаемых погрешностей, присваиваются буквы,
находящиеся ближе к началу алфавита.
. Для СИ, пределы допускаемой основной погрешности которых принято
выражать в форме относительной погрешности, обозначаются числами,
которые равны этим пределам, выраженным в процентах.
Обозначения класса точности наносят на циферблаты, щитки и корпуса СИ,
приводят в нормативных документах. Средствам измерений с несколькими
диапазонами измерений одной и той же физической величины или
предназначенным для измерений разных физических величин могут быть
присвоены различные классы точности для каждого диапазона или для каждой
измеряемой величины.
Классы точности присваиваются при разработке СИ по результатам
приемочных испытаний. В связи с тем, что при эксплуатации их
метрологические характеристики обычно ухудшаются, допускается понижать
класс точности по результатам поверки.
При подготовке и проведении высокоточных измерений в метрологической
практике учитывают влияние объекта измерения, субъекта, метода измерения,
средства измерения, условий измерения. Так, объект должен быть всесторонне
изучен; элемент субъективизма в результатах измерения должен быть сведен к
минимуму; учитывают факторы и условия, которые могут искажать результаты
измерений. Поэтому необходимо соблюдать методику выполнения измерений,
чтобы получить результаты с минимальной погрешностью. Такие методики
изложены в законе РФ «Об обеспечении единства измерений. А в 1997 году
начал действовать ГОСТ 8.563-96 «ГСИ. Методики выполнения измерений».
В моей повседневной работе мне не часто приходится сталкиваться с
различными средствами измерений. Однако приведу некоторые сравнительные
примеры, в которых о точности можно судить по порогу чувствительности.
Во многих современных продуктовых магазинах сейчас установлены
электронные весы, являющиеся рабочим средством измерений. Диапазон таких
весов – от 0 до 10 кг, а цена деления (если так можно выразиться для
электронной версии весов) или порог чувствительности составляет 1 грамм.
Таким образом, точность взвешивания достаточно высока и погрешность может
составлять 0.001 кг. И не только точность измерения, но и точность
расчетов с покупателями - ведь от веса продукта зависит его цена. К
сожалению, класс точности не был указан на корпусе, а сотрудники при таком
вопросе пришли в замешательство.
В продуктовых магазинах часто можно встретить и обыкновенные весы, на
которых взвешивают с помощью гирек, которые тоже являются рабочим
средством измерений. Я первый раз обратила внимание на такие весы и
увидела(!), что в нашем магазине они стоят на неровной поверхности. Дело в
том, что в корпус весов вмонтирован полый шарик, наполненный водой. Если
весы установлены ровно, то верхняя кромка воды (под действием физических
законов) располагается параллельно поверхности. В моем случае это явно
было не соблюдено. Диапазон весов – от 0 до 5 кг, а порог чувствительности
– 10 грамм. Из этого следует, что такие весы менее точные, нежели
описанные выше - электронные, так как погрешность может составлять 0.01
кг.
У нас на работе на складе установлены весы для взвешивания овощей. Эти
весы имеют диапазон от 0 до 200 кг, так что любой взрослый человек может
легко на них взвеситься. Порог чувствительности составляет 200 грамм и это
указано на циферблате. Помимо этого, на циферблате указано, что весы
изготовлены фирмой Suprema S.p.a., диапазон 0-200 кг, e-d=200 gr, серийный
номер № 122001/21 и индивидуальный номер №91097. Также там указан и класс
точности - III - для подобных средств измерений, относящихся к
профессиональному оборудованию. В паспорте этих весов указано, что классы
точности для данной продукции установлены от I до III, вероятно, согласно
нормативным документам, действующим в стране-производителе.
И, наконец, безмен, имеющий самый низкий класс точности и являющийся
рабочим средством измерения. С помощью этого средства можно произвести
скорее примерное взвешивание, т.к. цена деления составляет 0.5 кг и
погрешность при измерении будет очень значительна. Диапазон безмена – от 0
до 7 кг. Но даже при таком неточном средстве измерения, результат зависит
от некоторых факторов. В данном случае результат измерений напрямую
зависел от человека, производящего измерения. При повторном взвешивании
погрешность была очень высока и зависела от дрожания рук и от того,
насколько точно вертикально было положение безмена.
9. Возникновение и развитие математической статистики
Издавна в каждом государстве соответствующими органами власти собирались сведения о числе жителей по полу, возрасту, занятости в различных сферах труда, наличии различных воинов, вооружения, денежных средств, орудий труда, средств производства и т.д. Все эти и подобные им данные называются статистическими. С развитием государства и международных отношений возникла необходимость анализа статистических данных, их прогнозирование, обработка, оценка достоверности основанных на их анализе выводов и т.п. К решению таких задач стали привлекаться математики. Таким образом, в математике сформировалась новая область — математическая статистика, изучающая общие закономерности статистических данных или явлений и взаимосвязи между ними.
Сфера применения математической статистики распространилась во многие, особенно экспериментальные, науки. Так появились экономическая статистика, медицинская статистика, биологическая статистика, статистическая физика и т.д. С появлением быстродействующих ЭВМ возможность применения математической статистики в различных сферах деятельности человека постоянно возрастает. Расширяется ее приложение и к области физической культуры и спорта. В связи с этим основные понятия, положения и некоторые методы математической статистики рассматриваются в курсе “Спортивная метрология”. Остановимся на некоторых основных понятиях математической статистики.
Статистические данные
В настоящее время под термином "статистические данные" понимают все собранные сведения, которые в дальнейшем подвергаются статистической обработке. В различной литературе их еще называют: переменные, варианты, величины, даты и т.д. Все статистические данные можно разделить на: качественные, труднодоступные для измерения (имеется, не имеется; больше, меньше; сильно, слабо; красный, черный; мужской, женский и т.д.), и количественные , которые можно измерить и представить в виде числа общих мер (2 кг, 3 м, 10 раз, 15 с и т.д.); точные , величина или качество которых не вызывают сомнений (в группе 6 человек, 5 столов, деревянный, металлический, мужской, женский и т.д.), и приближенные , величина или качество которых вызывает сомнение (все измерения: рост 170 см, вес 56 кг, результат бега на 100 м - 10,3 с и т.д.; близкие понятия — синий, голубой, мокрый, влажный и т.д.); определенные (детерминированные), причины появления, не появления или изменения которых известны (2 + 3 = 5, подброшенный вверх камень обязательно будет иметь вертикальную скорость, равную 0 и т.д.), и случайные , которые могут появляться и не появляться или не все причины изменения которых известны (пойдет дождь или нет, родится девочка или мальчик, команда выиграет или нет, в беге на 100 м — 12,2 с, принятая нагрузка вредна или нет). В большинстве случаев в физической культуре и спорте мы имеем дело с приближенными случайными данными.
Статистические признаки, совокупности
Общее свойство, присущее нескольким статистическим данным, называют их статистическим признаком . Например, рост игроков команды, результат бега на 100 м, принадлежность к виду спорта, частота сердечных сокращений и т.д.
Статистической совокупностью называют несколько статистических данных, объединенных в группу хотя бы одним статистическим признаком. Например, 7.50, 7.30, 7.21, 7.77 — результаты прыжка в длину в метрах у одного спортсмена; 10, 12, 15, 11, 11 — результаты подтягивания на перекладине пяти студентов и т.д. Число данных в статистической совокупности называют ее объемом и обозначают n . Различают следующие совокупности:
бесконечные — n 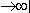 (масса планет Вселенной, число молекул и т.д.);
(масса планет Вселенной, число молекул и т.д.);
конечные — n - конечное число;
большие — n > 30;
малые — n 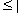 30;
30;
генеральные — содержащие все данные, обусловленные постановкой задачи;
выборочные — части генеральных совокупностей.
Например, пусть рост студентов 17-22 лет в РФ — генеральная совокупность, тогда рост студентов КГАФК, всех студентов города Краснодара или студентов II курса — выборки.
Кривая нормального распределения
При анализе распределения результатов измерений всегда делают предположение о том распределении, которое имела бы выборка, если бы число измерений было очень большим. Такое распределение (очень большой выборки) называют распределением генеральной совокупности или теоретическим , а распределение экспериментального ряда измерений — эмпирическим.
Теоретическое распределение большинства результатов измерений описывается формулой нормального распределения, которая впервые была найдена английским математиком Муавром в
Это математическое выражение распределения позволяет получить в виде графика кривую нормального распределения (рис.3), которая симметрична относительно центра группирования (обычно это значение , моды или медианы). Эта кривая может быть получена из полигона распределения при бесконечно большом числе наблюдений и интервалов. Заштрихованная область графика на рисунке 3 отражает процент результатов измерений, находящихся между значениями х1 и х2.
Рис. 3. Кривая нормального распределения.
Введя обозначение, которое называется нормированным или стандартизованным отклонением, получают выражение для нормированного распределения:
На рисунке 4 представлен график этого выражения. Он примечателен тем, что для него =0 и s =1 (результат нормировки). Вся площадь, заключенная под кривой, равна 1, т.е. она отражает все 100% результатов измерений. Для теории педагогических оценок и особенно для построения шкал представляет интерес процент результатов, лежащих в различном диапазоне варьирования, или колеблемости.
function PlayMyFlash(cmd){ Norm_.SetVariable("Counter", cmd); Norm_.GotoFrame(2); Norm_.Play(); } Кривая нормированного распределения с процентным выражением распределений относительных и накопленных частностей:
под первой осью абсцисс — среднее квадратическое отклонение;
под второй (нижней) — накопленный процент результатов. Другими словами, отклонения, большего, чем 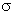 , от следует ожидать примерно в одном случае из трех; отклонения, большего, чем 2
, от следует ожидать примерно в одном случае из трех; отклонения, большего, чем 2 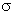 , — в четырех-пяти случаях из 100, отклонения, большего, чем 3
, — в четырех-пяти случаях из 100, отклонения, большего, чем 3 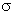 , — в трех из 1000. Последнее соотношение для нормального распределения называют "правилом трех сигм" и используют при исключении сильно отклоняющихся "ошибочных" результатов измерений.
, — в трех из 1000. Последнее соотношение для нормального распределения называют "правилом трех сигм" и используют при исключении сильно отклоняющихся "ошибочных" результатов измерений.
Виды представления статистических данных
После того, как определена выборка и стали известны ее статистические данные (варианты, даты, элементы и т.д.), возникает необходимость представить эти данные в удобном для решения задачи виде. На практике используют много различных видов представления статистических данных. Наиболее часто употребляют следующие:
а) текстовый вид;
б) табличный вид;
в) вариационный ряд;
г) графический вид.
Если при статистической обработке совокупности безразлично в какой последовательности записывать данные, то бывает удобным расположить эти данные (варианты) в соответствии с их значением либо по возрастанию xi ~ 2, 3, 3, 5, 5, 6, 6, 6, 6, 7 (неубывающая совокупность), либо по убыванию xi ~ 7, 6, 6, 6, 6, 5, 5, 3, 3, 3, 2 (невозростающая совокупность). Этот процесс называется ранжированием . А место каждой варианты в ранжированном ряду называется рангом .
10.11. Выборка (выборочная совокупность) - часть объектов из генеральной совокупности, отобранных для изучения, с целью получения информации о всей генеральной совокупности.
Число объектов, составляющих выборочную совокупность, называется объемом выборки.
Методы математической статистики позволяют оценить случайную ошибку изучаемых признаков выборки определенного объема. Также можно решить обратную задачу - определить объем выборки, удовлетворяющий заданным требованиям точности.
Кроме объема выборки, существенную роль играет способ формирования выборки. Не вдаваясь в детали, можно отметить, что выборка, которая сохраняет все свойства генеральной совокупности, называется репрезентативной выборкой. Свойство репрезентативности - необходимое условие для того, чтобы выводы, сделанные для выборочной совокупности, можно было распространить на генеральную совокупность.
Основа выборки - это описание (перечень) всех единиц наблюдения исходной совокупности, который используется для отбора единиц отбора и наблюдения. Чаще всего понятие применяется к ед. наблюдения.
Если выборка содержит все возможные результаты измерений, то эти результаты представляют собой генеральную совокупность. Отметим, что генеральная совокупность измерений может содержать как бесконечное число элементов (как в данном примере), так и конечное число элементов. Обычно выборка содержит малую часть генеральной совокупности и поэтому лишь приближенно характеризует свойства генеральной совокупности. Поскольку полной статистической характеристикой СВ является ее распределение, для описания выборки используется аналог распределения для случая выборочных данных, который называется гистограммой. Для построения гистограммы выполним следующие действия.
Расположим числа в выборке в порядке возрастания их величин. В результате получим ранжированный статистический ряд.
Объем выборки - количественный параметр выборочной совокупности, число единиц наблюдения, подлежащих изучению (число респондентов).
Существует три способа определения объема выборки:
1. по формулам для случайно-вероятностной выборки;
2. по таблицам сопряженности;
3. использование опыта прошлых исследований;
Репрезентативность выборки - основное свойство выборки, способность ее воспроизводить и представлять характеристики ГС. Выборка должна быть моделью ГС. Это свойство воспроизводить статистическую структуру ГС в отношении изучаемых характеристик. Она является основным условием формирования и проектирования выборки.
12. Анализ вариационных рядов упрощается при графическом представлении. Рассмотрим основные графики вариационного ряда.
1. Полигон распределения На графике ѕ это кривая, отражающая по оси абсцисс (Х) средние значения классов, а по оси ординат (Y ) ѕ частоту накопления величин в каждом классе.
2. Гистограмма распределения График, выполненный в прямоугольной системе координат и отражающий по оси ординат (Y ) частоту накопления величин в классе, а по оси абсцисс (Х) - границы классов.
Графическое представление результатов измерений не только существенно облегчает анализ и выявление скрытых закономерностей, но и позволяет правильно выбрать последующие статистические характеристики и методы.
Гистограмма - 1. столбчатая диаграмма; графическое изображение изменений какой-либо величины; 2. техническое средство анализа динамики биржевых цен методом построения графиков в системе координат; диапазон изменения цены может быть выражен линиями, соединяющими низшую и высшую цены.
При дискретной вариации признака графиком вариационного ряда служит полигон распределения (рис 49). Для его построения на оси абсцисс отмечают точки, соответствующие величине вариантов значений признака - x, из них восстанавливаются перпендикуляры, длина которых соответствует частоте (частости) этих вариантов - f по принятому масштабу на оси ординат. Вершины перпендикуляров в последовательном порядке соединяются отрезками прямых. Для замыкания полигона (получения замкнутого многоугольника) из крайних вершины опускаются перпендикуляры на ось абсцисс.
Графически полигон распределения представляет распределение совокупности по признаку х.
В интервальном вариационном ряду для преобразования гистограммы в полигон середины верхних сторон прямоугольников соединяют отрезками прямой, и две крайние точки прямоугольников замыкаются по оси абсцисс на середине интервалов, в которых частоты равны нулю.
На рис. 50 предоставлено графическое изображение построенного интервального вариационного ряда в виде гистограммы и полигона частот.
13. Частный случай, при котором среднее равно нулю, а дисперсия - единице, называется стандартным нормальным распределением; соответствующим образом распределенные переменные обычно обозначаются Z.
Нормальное распределение часто используется для описания поведения остаточного члена в регрессионном анализе и позволяет рассчитать обычные проверочные статистики, т.е. t-статистику, f-статистику и т.д.
Нормальное распределение
Многочисленные методы, с помощью которых обрабатываются переменные, относящиеся к интервальной шкале, исходят из гипотезы, что их значения подчиняются нормальному распределению. При таком распределении большая часть значений группируется около некоторого среднего значения, по обе стороны от которого частота наблюдений равномерно снижается.
В качестве примера рассмотрим нормальное распределение возраста, которое строится по данным исследований гипертонии (файл hyper.sav) с помощью команд меню Graphs (Графы) Histogramm... (Гистограмма) (см. рис. 5.1).
На диаграмме нанесена кривая нормального распределения (Колокол Гаусса). Реальное распределение в большей или меньшей степени отклоняется от этой идеальной кривой. Выборки, строго подчиняющиеся нормальному распределению, на практике, как правило, не встречаются. Поэтому почти всегда необходимо выяснить, можно ли реальное распределение считать нормальным и насколько значительно заданное распределение отличается от нормального.
Перед применением любого метода, который предполагает существование нормального распределения, наличие последнего нужно проверять в первую очередь. Классическим примером статистического теста, который исходит из гипотезы о нормальном распределении, можно назвать t-тест Стьюдента, с помощью которого сравнивают две независимые выборки. Если же данные не подчиняются нормальному распределению, следует использовать соответствующий непараметрический тест, в случае двух независимых выборок — U-тест Манна и Уитни.
14.Теоретические сведения
Наиболее распространенными характеристиками совокупности являются:
1) среднее арифметическое
2) среднее квадратическое (или стандартное) отклонение
3) стандартная ошибка среднего арифметического
4) коэффициент вариации (V).
Средним арифметическим называется частное от деления суммы всех значений вариант рассматриваемой совокупности на их число (n):
Среднее арифметическое обладает следующими свойствами:
а) измеряется в тех же единицах, что и основные варианты;
б) если каждое число совокупности уменьшить (увеличить) на одно и то же число, то ее среднее уменьшится (увеличится) на это же число;
в) если каждое число совокупности увеличить (уменьшить) в несколько раз, то ее среднее увеличится (уменьшится) в такое же число раз;
г) сумма отклонений статистических данных совокупности от их точного среднего всегда равна нулю:
Среднее квадратическое (или стандартное) отклонение  . Основной мерой статистического измерения изменчивости признака у членов совокупности служит среднее квадратическое отклонение
. Основной мерой статистического измерения изменчивости признака у членов совокупности служит среднее квадратическое отклонение  (сигма) или, как часто ее называют, стандартное отклонение. Теория вариационной статистики показала, что для характеристики любой генеральной совокупности, имеющей нормальный тип распределения достаточно знать два параметра: среднюю арифметическую и среднее квадратическое отклонение. Эти параметры заранее не известны и их оценивают с помощью выборочной средней арифметической и выборочного стандартного отклонения, которые вычисляются при обработке случайной выборки.
(сигма) или, как часто ее называют, стандартное отклонение. Теория вариационной статистики показала, что для характеристики любой генеральной совокупности, имеющей нормальный тип распределения достаточно знать два параметра: среднюю арифметическую и среднее квадратическое отклонение. Эти параметры заранее не известны и их оценивают с помощью выборочной средней арифметической и выборочного стандартного отклонения, которые вычисляются при обработке случайной выборки.
В основе среднего квадратического отклонения лежит сопоставление каждой варианты  со средней арифметической данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений
со средней арифметической данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений  ), имеющих знак " - ", будет погашаться суммой отклонений, имеющих знак
), имеющих знак " - ", будет погашаться суммой отклонений, имеющих знак  Отклонение вариант от своей средней арифметической выражает изменчивость признака. Если бы изменчивость признака у членов совокупности отсутствовала, тогда разность
Отклонение вариант от своей средней арифметической выражает изменчивость признака. Если бы изменчивость признака у членов совокупности отсутствовала, тогда разность  Но т.к.
Но т.к.  всегда равна нулю, то для измерения изменчивости берут отклонение в квадрате, т.е.
всегда равна нулю, то для измерения изменчивости берут отклонение в квадрате, т.е.  Если просуммировать квадраты отклонений, то эта сумма не будет равна нулю. А чтобы получить коэффициент, способный измерить изменчивость, берут среднее отклонение из выражения: Величина
Если просуммировать квадраты отклонений, то эта сумма не будет равна нулю. А чтобы получить коэффициент, способный измерить изменчивость, берут среднее отклонение из выражения: Величина  называется девиатой (или взвешенной дисперсией), вариансой (или средним квадратом). Тогда среднее квадратическое отклонение имеет следующую формулу:
называется девиатой (или взвешенной дисперсией), вариансой (или средним квадратом). Тогда среднее квадратическое отклонение имеет следующую формулу:
Свойства среднего квадратического (стандартного) отклонения:
1. Стандартное отклонение всегда измеряется в тех же единицах измерения, что и основные варианты.
2. Чем больше  , тем больше изменчивость признака.
, тем больше изменчивость признака.
3. В вариационных рядах с нормальным распределением частот 99,7% всех членов совокупности находящихся в границах от  , которые отстоят от средней арифметической на величину от
, которые отстоят от средней арифметической на величину от  . За пределами
. За пределами  находятся только 0,3% всех членов совокупности.
находятся только 0,3% всех членов совокупности.
4. При вычислении стандартное отклонение определяют с точностью на один десятичный знак больше, чем точность, которую применяют для вычисления средней арифметической для того же ряда.
3. Стандартная ошибка средней арифметической или ошибка репрезентативности  характеризует колебания средней. При этом необходимо отметить, что чем больше объем выборки, тем меньше разброс средних величин.
характеризует колебания средней. При этом необходимо отметить, что чем больше объем выборки, тем меньше разброс средних величин.
Стандартная ошибка средней вычисляется по формуле:
В современной научной литературе средняя арифметическая представляется вместе с ошибкой репрезентативности:
Коэффициент вариации (V). Изложенные выше характеристики совокупности (средняя арифметическая и среднее квадратическое отклонение) имеют один недостаток: они дают показатель изменчивости признака в именованных величинах, а не в относительных. Поэтому сопоставление (или сравнение) разноименных признаков по этим параметрам невозможно.
В этом случае удобно пользоваться коэффициентом изменчивости признака, который выражается в относительных величинах, а именно в процентах, и вычисляется по формуле:
Чем больше V, тем более изменчив признак. Значения коэффициента вариации, невыходящие за пределы 10%, принято считать нормальными.
15. СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ - один из показателей центра распределения для количественных переменных (см.); обозначается x. Представляет собой значение переменной, полученной в результате деления суммы всех ее значений на объем выборки
Мода .Мода представляет из себя наиболее часто встречающиеся значения распределения. При этом следует помнить о различиях модального значения для дисперсных и непрерывных характеристик. В первом случае модой является варианта с наибольшей частотой - скажем, максимальный процент выборов в вопросе с номинальной шкалой.Если же речь идет об интервальном ряде, представляющем собой непрерывную характеристику признака, то модальным значением будет являться группа снаибольшим числом наблюдений.
Медиана. Медианой именуется центральное (серединное) наблюдение в ряду распределения. Так, в ряду из 203 наблюдений медианным будет являться 102. При четном числе наблюдений медианой является среднее арифметическое из тех двух наблюдений, которые делят ряд на две равные части (при n=202, это были бы №№ 101 и 102).Для ряда логических процедур требуется более дробное деление ряда, поэтомукроме медианы выделяются по мере необходимости децили (1/10 ряда), квинтили(1/5) и квартили (1/4). Таким образом, любой ряд может быть разбит на 2 частимедианой, на 4 - квартилями, на 5 - квинтилями, на 10 - децилями.Продемонстрируем эти значения, а также ряд осуществляемых с ними процедур нагипотетическом примере. Допустим, при опросе родителей учащихся был использовантрадиционный вопрос о размере душевого дохода в семье(см. таб1).
Для небольшой выборки М. может быть найдена как середина ряда упорядоченных значений переменной (указываются все повторяющиеся значения). Например, в ряду из 9 значений 27 29 30 30 32 37 46 50 52 М. будет число 32, расположенное в центре ряда (Ме = 32
16. Размах
Величина его целиком зависит от случайности распределения крайних членов ряда, и значение подавляющего большинства членов ряда не учитывается, в то время как вариация связана с каждым значением члена ряда.
Такие показатели, которые представляют собой средние, полученные из отклонений индивидуальных значений признака от их средней величины, лишены этого недостатка.
Между индивидуальными отклонениями от средней и колеблемостью конкретного признака существует прямая зависимость. Чем сильнее колеблемость, тем больше абсолютные размеры отклонений от средней.
Дисперсия
ДИСПЕРСИЯ - один из показателей вариации количественной переменной (см.), равен отношению суммы квадратов (см.) отклонений от среднего арифметического SSx к числу степеней свободы (см.) данной суммы квадратов (n - 1); в отличие от суммы квадратов, измеряет "чистую" вариацию переменной, не зависящую от объема выборки.
Особая ценность Д., вычисленной по выборке, состоит в том, что она является несмещенной оценкой (см.) Д. генеральной совокупности - ср.: выборочное стандартное отклонение (см.) является состоятельной, но смещенной оценкой стандартного отклонения генеральной совокупности.
Дисперсия - наиболее употребительная мера отклонения от среднего.
17. СТАНДАРТНОЕ ОТКЛОНЕНИЕ - наиболее распространенный показатель вариации количественной переменной (см.), измеряет "средний" разброс значений переменной относительно ее среднего арифметического (см.) в тех же единицах измерения, что и сама переменная; равен корню квадратному из дисперсии (см.) (см. также Сумма квадратов, Коэффициент вариации). Используется при нахождении стандартной ошибки (см.) среднего арифметического, построении доверительных интервалов (см.), статистической проверке гипотез (см.), измерении линейных связей между переменными и т.п.
Например, s = 5 (см) для переменной "рост" будет означать, что рост респондентов, попавших в выборку, отклоняется от среднего арифметического в среднем на ?5 см.
КОЭФФИЦИЕНТ ВАРИАЦИИ - показатель вариации количественной переменной (см.), измеряющий стандартное отклонение (см.) в процентах от среднего арифметического (см.):
V = s / x × 100%.
Применяется в сравнительном анализе и метанализе для сопоставления результатов, полученных для разных переменных, разных совокупностей объектов, в разных исследованиях.
18. Понятие функциональной зависимости
Будем говорить, что между двумя признаками X и Y существует функциональная зависимость (взаимосвязь), при которой каждому значению одного из них соответствует одно или несколько строго определенных значений другого.
Например, в функции у = 2 * х каждому значению х соответствует в два раза большее значение у . В функции  каждому значению у соответствует 2 определенных значения х .
каждому значению у соответствует 2 определенных значения х .
Понятие корреляционной зависимости и ее направленности
Будем говорить, что между двумя признаками Х и У существует корреляционная зависимость (взаимосвязь), при которой с изменением одного признака изменяется и другой, но каждому значению признака Х могут соответствовать разные, заранее непредсказуемые значения признака У, и наоборот.
Для различия направленности влияния одного признака на другой введены понятия положительной и отрицательной связи.
Если с увеличением (уменьшением) одного признака в основном увеличиваются (уменьшаются) значения другого, то такая корреляционная связь называется прямой или положительной.
Если с увеличением (уменьшением) одного признака в основном уменьшаются (увеличиваются) значения другого, то такая корреляционная связь называется обратной или отрицательной.
19. График корреляционного поля.
Будем называть корреляционным полем зону разброса таким образом полученных точек на графике. Визуально анализируя корреляционное поле на рисунке 8, можно заметить, что оно как бы вытянуто вдоль какой-либо прямой линии. Такая картина характерна для так называемой линейной корреляционной взаимосвязи между признаками. При этом можно в общем предположить, что с увеличением конечной скорости разбега увеличивается и длина прыжка, и наоборот. Т.е. между рассматриваемыми признаками наблюдается прямая (положительная) взаимосвязь.
Наряду с этим примером из множества других возможных корреляционных полей можно выделить следующие (рис.9-11):
На рисунке 9 тоже просматривается линейная взаимосвязь, но с увеличением значений одного признака, уменьшаются значения другого, и наоборот, т.е. связь обратная или отрицательная. Можно предположить, что на рисунке 11 точки корреляционного поля разбросаны около какой-то кривой линии. В таком случае говорят, что между признаками существует криволинейная корреляционная связь.
В отношении корреляционного поля, изображенного на рисунке 10, нельзя сказать, что точки располагаются вдоль какой-то прямой или кривой линии, оно имеет сферическую форму. В этом случае говорят, что признаки Х и Y не зависят друг от друга.
Кроме этого по корреляционному полю можно примерно судить о тесноте корреляционной связи, если эта связь существует. Здесь говорят: чем меньше точки разбросаны около воображаемой усредненной линии, тем теснее корреляционная связь между рассматриваемыми признаками.
Визуальный анализ корреляционных полей помогает разобраться в сущности корреляционной взаимосвязи, позволяет высказать предположение о наличии, направленности и тесноте связи. Но точно сказать, имеется связь между признаками или нет, линейная связь или криволинейная, тесная связь (достоверная) или слабая (недостоверная), с помощью этого метода нельзя. Наиболее точным методом выявления и оценки линейной взаимосвязи между признаками является метод определения различных корреляционных показателей по статистическим данным.
20. Задача корреляционного анализа сводится к установлению направления и формы связи между признаками, измерению ее тесноты и к оценке достоверности выборочных показателей корреляции.
Корреляционная связь между признаками может быть линейной и криволинейной (нелинейной), положительной и отрицательной.
Прямая корреляция отражает однотипность в изменении признаков: с увеличением значений первого признака увеличиваются значения и другого, или с уменьшением первого уменьшается второй.
Обратная корреляция указывает на увеличение первого признака при уменьшении второго или уменьшение первого признака при увеличении второго.
Например, больший прыжок и большее количество тренировок — прямая корреляция, уменьшение времени, затраченного на преодоление дистанции, и большее количество тренировок — обратная корреляция.
21. Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции — это мера линейной зависимости двух случайных величин.
КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ, R², - оценка качества ("объясняющей способности") уравнения регрессии, доля дисперсии объясненной (см.) зависимой переменной у:
R² = 1 - ∑(yi - ŷi)² / ∑(yi - y)² ,
где yi - наблюдаемое значение зависимой переменной y, ŷi - значение зависимой переменной, предсказанное по уравнению регрессии, y - среднее арифметическое зависимой переменной.
Для регрессии линейной парной (см.) К.Д. равен квадрату коэффициента линейной корреляции Пирсона (см.) r². Таким образом, если коэффициент линейной корреляции r = 0,5, то r² = 0,25, т.е. различия в значениях зависимой переменной y на 25% объясняются различиями в значениях независимой переменной x (и на 75% - факторами, не учтенными в уравнении регрессии).
Для регрессии линейной множественной (см.) коэффициент множественной детерминации равен квадрату коэффициента корреляции множественной (см.) R².
Теснота регрессионной связи измеряется коэффициентом детерминации (см.), который интерпретируется как доля дисперсии зависимой переменной y, объясненная независимыми переменными x1, x2,... xk (см. Дисперсия объясненная). Для парной линейной регрессии коэффициент детерминации равен квадрату коэффициента линейной корреляции Пирсона (см.) r², для множественной линейной регрессии - квадрату коэффициента корреляции множественной (см.) R².