Раскрытие неопределенностей

Модуль 2.

Тема 12. Предел функции

 

12.1.Окрестности.

12.2.Определение предела функции. Варианты определения

12.3.Бесконечно малые. Бесконечно большие

12.4.Раскрытие неопределенностей

 

 

Программные положения

Понятие предела, наряду с понятием функциональной зависимости, есть одна из важнейших концепций математического анализа.

 

Методические рекомендации

Внимательно прочитайте материал лекции. Выпишите варианты определения предела функции для конечных и бесконечных случаев. Выполните упражнения. Уделите внимание понятию бесконечно малой.

 

Литература

А.В.Дорофева «Высшая математика» Глава 6 «Теория пределов» стр. 122-160

Б.П.Демидович, В.А.Кудрявцев Краткий курс высшей математики Глава VII «Теория пределов» стр.95-133

А.Н. Кричивец, Е.В. Шикин, А.Г.Дьячков Математика для психологов . Часть II Глава I «Исходные идеи дифференциального исчисления» 1.1 «Истрико-философский экскурс» стр.330-336 1.2. «Предел и производная» 2.1. «Техника и » (стр. 148-155)

Дополнительно

А.Я.Хинчин «8 лекций по математическому анализу» Лекция II «Пределы» стр.33-59

Р.Курант, Г.Роббинс «Что такое математика?» Глава VI, Введение, § 1 «Независимые переменные и функции» (стр.300-317), §2 «Пределы» (стр.317-330), §3 «Пределы при непрерывном приближении» (стр.330-337); Глава VIII «Обозначения Лейбница и бесконечно малые» § 4 стр. 461-463

 

 

Контрольные вопросы

1. Что такое окрестность точки? Проколотая окрестность?

2. Что такое (конечный) предел функции в (конечной ) точке? Бесконечный предел? В бесконечно удаленной точке?

Выпишите определения предела при конечных и бесконечных А и x₀. Приведите примеры.

3. Дайте определение односторонних пределов

4. Выпишите замечательные пределы

5. Приведите примеры несуществования предела функции в точке

6. Какая функция называется бесконечно малой?

7. Что называется раскрытием неопределенностей?

8. Найдите пределы

 

 

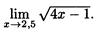
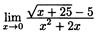
Окрестности

 

Определения 12.1.

 

Пусть e — некоторое положительное число. e-окрестностью точки x₀ называется множество всех точек x, принадлежащих промежутку (x₀ e, x₀ + e), кроме самой точки x₀. Принадлежность точки x eокрестности точки можно выразить с помощью двойного неравенства

0 < êx – x₀ç < e.

Интервал (x₀ e, x₀ + e) \ { x₀} называется проколотой окрестностью точки x₀ (интервал с центром в точке x₀ без самой этой точки)

Если требуется определить окрестности точек ±, это делается следующим образом: (>0)

x₀ = + Ue (+)= (, +]

x₀ = - Ue (- ) = [- , )

Обозначение: U_e (a) - e-окрестность точки а, - проколотая окрестность.

Традиционно окрестности точек по оси y обозначают как -окрестности, а по оси х – -окрестностями (U (a))

 

Определение предела функции. Варианты определения

Рассмотрим функцию y = x² в точке x₀ = 2. Значение функции в этой точке равно 4.

Отметим одну особенность поведения функции в этой точке. Можно

выбрать какое-либо поло­жительное число eи построить e-окрестность точки y₀ = 4. Очевидно, что найдется такая окрестность точки x₀ = 2 (на рисунке 1 эта окрестность имеет радиус d) , что если x будет лежать в этой окрестности, то соответствующее значение y, равное x², попадет в e-окрестность точки y₀ = 4. Это заключение справедливо для любого, сколь угодно малого числа e. Здесь точка x₀ = 2 выбрана произвольно. Можно было бы для данной функции выбрать любую другую точку и сделать подобное заключение.

Рассмотрим функцию .Эта функция не определена в точке x₀ = 2. При x₀ ¹ 2 её можно преобразовать:

.

График функции представлен на рисунке 2. Хотя исходная функция не определена в точке x₀ = 2 и естественно не равна 3 в этой точке, точка y₀ = 3 имеет характерную особенность. Выбрав положитель­ное число e, можно утверждать, что если рассматривать значения x, расположенные достаточно близко к точке x₀ = 2 (или лежащие в некоторой окрестности точки x₀ = 2, причем радиус этой окрестности зависит от e), то соответствующие значения y попадут в e-окрестность точки y₀ = 3. Всё сказанное остаётся справедливым независимо от того, насколько малым выбрано положительное число e.

 

 

Определение 12.2(1).

 

Введем понятие предела функции. Число A называется пределом функции y = f(x) в точке x₀ (иногда говорят, при x, стремящемся к x₀, х x₀) если для любого положительного числа e можно найти такое положительное число d, что для всех x из проколотой d-окрестности точки x₀ соответствующие значения y попадают в e-окрестность точки y = A.

Можно сформулировать определение предела функции по-другому. Число A называется пределом функции y = f(x) в точке x₀, если для любого положительного числа e можно найти такое положительное число d, что для всех x, удовлетворяющих условию

0 < êx – x₀ê < d,

выполняется условие

êy – Aê < e.

Тот факт, что A есть предел функции y = f(x) в точке x = x₀, записывается формулой или f(x) A при x x₀

 

Замечание 12.2.

Предел функции в некоторой точке совсем не обязан существовать.

Как видно из второго из рассмотренных выше примеров, для того, чтобы функция имела предел в точке x = x₀, не требуется, чтобы она была определена в этой точке (это отражается в требовании принадлежности точки x₀ проколотой окрестности в определении предела)

Рассмотрим функцию . Очевидно, что если x > 0, то y = 2^x; если x < 0, то y = –2^x; при x = 0 функция не определена.

График функции изображен на рисунке 3. Легко убедиться в том, что, согласно приведенному выше определению предела, эта функция в точке x = 0 предела не имеет.

 

Также не существует предела

(см.рис.4)

Рис.4.

 

Пример 12.2(1).

 

Показать, что

Зафиксируем произвольное > 0. Требуется по этому найти такое > 0, чтобы из условия x x₀, | x —x₀| < , т.е. из 0 < |х — 2| < вытекало бы неравенство |f(x) —A|<, т.е. |(2х + 1) – 5 | < .

 

Последнее неравенство приводится к виду |2(х — 2)| < , т.е.

|х — 2| < /2. Отсюда следует, что если взять = /2 то неравенство |х — 2| < будет автоматически влечь за собой неравенство |f(х) — 5| < (это значит, что для всех х, для которых верно первое неравенство, будет верно и второе). В соответствии со определением предела функции это означает, что .

 

Свойства предела функции.

1. Функция не может иметь в одной точке два разных предела.

2. , если C — постоянная функция.

3. Если существует и C — постоянная функция, то

.

4. Если существуют и , то существует , равный , а также существует , равный . Если при этом , то существует , равный .

Примеры 12.2(2)

1.

2.Пример на раскрытие неопределенности ( о раскрытии неопределенностей см. 12.4): рассмотрим случай, когда числитель и знаменатель стремятся к нулю в рассматриваемой точке.

сократить дробь можно, т.к. мы не рассматриваем предел самой точке х=2. В полученной дроби знаменатель уже не стремится к нулю при х 2, поэтому можно применять утверждение о пределе частного:

и, соответственно,

3. Еще один способ раскрытия неопределенностей – избавление от корня путем получения разности квадратов(в данном случае - )

 

 

4.. Рассмотрим случай другой неопределенности, когда числитель и знаменатель стремятся к бесконечности, т.е. неопределенность .

Числитель и знаменатель дроби здесь удобно поделить на х (это возможно, т.к. х ненулевой) и воспользоваться стремлением к нулю :

Определение 12.2(2) Односторонние пределы

Число B называется пределом функцииf(x)в точкеaсправа (это записывается в виде формулы ), если для любого поло­жительного числа e найдется положительное число d, такое что из условия 0 < x – a < d будет следовать êB –f(x) ê < e. Другое обозначение этого предела

Согласно приведенному определению . Отметим, что обыкновенного предела функция в точке x = 0 не имеет.

Число С называется пределом функцииf(x)в точкеbслева (это записывается в виде формулы ), если для любого поло­жительного числа e найдется положительное число d такое, что из условия 0 < b – x < d будет следовать êC – f(x)ê < e. Другое обозначение этого предела

Очевидно, что функция (её график, изображен на рисунке 3) имеет два односторонних предела в точке x = 0:

; .

Теорема 12.2 (без доказательства) связь понятия предела функции в точке и односторонних пределов.

 

Для того, чтобы выполнялось равенство , необходимо и достаточно, чтобы одновременно выполнялись два равенства:

;

В дальнейшем нам понадобятся понятия предела функции в бесконечно удалённых точках. Рассмотрим сначала функцию f(x), определенную на полубесконечном промежутке (d; ¥). Число А называется пределом функции f(x) при х, стремящемся к бесконечности:

,

если для любого положительного числа e можно найти такое положительное число , что для всех чисел х, превосходящих , выполняется условие:

½f(x) – A½ < e.

Пусть теперь функция f(x) определена на полубесконечном промежутке
(–¥; d). Число А называется пределом функции f(x) при х, стремящемся к минус бесконечности:

,

если для любого положительного числа e можно найти такое положительное число , что для всех чисел х, меньших, чем – , выполняется условие:

½f(x) – A½ < e.

 

Если теперь + равен А (т.е. f(x) + при x x₀)

+ называется пределом функции f(x) при x x₀, если для любого положительного числа e можно найти такое положительное число d, что для всех x, удовлетворяющих условию 0 < êx – x₀ê < d, выполняется условие

f(x) > e.

Если теперь А = - (т.е. f(x) - при x x₀)

+ называется пределом функции f(x) при x x₀, если для любого положительного числа e можно найти такое положительное число d, что для всех x, удовлетворяющих условию 0 < êx – x₀ê < d, выполняется условие

f(x) < - e.

Отметим без доказательства два замечательных предела.

1. . Геометрический смысл этой формулы заключается в том, что прямая является касательной к графику функции в точке .

2. . Здесь e — иррациональное число, приблизительно равное 2,72.

Другой вариант записи этого замечательного предела, достигаемый очевидной заменой переменной:

 

Примеры 12.2

1. Найти

2. Найти

Замечание 12.2.

 

Часто используются такие следствия из замечательных пределов:

 

 

Бесконечно малые

 

Определение 12.3.

 

 

 

При решении многих задач используются следующие эквивалентности:

 

 

Таким образом, предел произведения или частного двух бесконечно малых не меняется при замене любой из них на эквивалентную бесконечно малую.

 

Примеры 12.3.

1.

,поскольку(следствие из 1-го замечательного предела)

2.

, поскольку при

 

 

Определение 12.3(2)

Функция f называется бесконечно большой в точке а , если |f| +. Если f+, f – бесконечно большая, f - , f – бесконечно большая. Но, даже если f не имеет предела, как, например, функция f(x) = x (-1)^[x], она является бесконечно большой, поскольку

|f| +.

Очевидно, что f – бесконечно большая в точке x₀ тогда и только тогда, когда 1/f - бесконечно малая в x₀.

 

Раскрытие неопределенностей

 

Бывают случаи, когда невозможно предугадать значение предела, если речь идет о функциях - результатах действий над бесконечно большими и бесконечно малыми.

Таковыми являются, например, пределы (бесконечно большая бесконечно большая), бесконечно большая / бесконечно большая, бесконечно малая/бесконечно малая, сумма двух бесконечно больших с разными знаками.

Например, если в точке а f +, g- , нельзя предсказать предел суммы: в одном случае этот предел может быть равен одному числу, в другом – другому, а может и вообще не существовать. Нужны дополнительные исследования.

Эти исследования называют раскрытием (соответствующей) неопределенности .

Неопределенности эти обозначаются: - .

 

Примеры 12.4.

1.-, xa

а=+

f(x)=x+10 +

g(x)= -x -

f+g = 10 10

2. .-, xa

а=+

f(x)=x+sin x+

g(x)=-x -

f+g=sin x, предела не имеет

3.

а=+

f(x) = 1/x 0

g(x) = x+

fg = 11

a

f(x) = 20/x 0

g(x) = x+

fg = 2020