Линейные дифференциальные уравнения первого порядка
РЕФЕРАТ
На тему: “дифференциальные уравнения второго порядка”.
Выполнил: студент 205 группы
специальности “фармация”
Петухов.М.С
Проверила: Максимова .И.В
г.Ижевск 2012
Содержание
1.Введение – 1стр
2.Основные понятия – 2стр
3.Линейные ДУ первого порядка – 2стр
4.Линейные ДУ второго порядка с постоянными коэффициентами – 3стр
5.ДУ в частных производных – 7стр
6.Обыкновенные ДУ – 7стр
7.ДУ с частными производными с особенностями в коэффициентах – 8стр
8.Дифференцированные Уравнения – 9стр
9.Литература – 10стр
10. Заключение – 11стр
Введение
Определение производной от данной функции составляет прямую зада-
чу исчисления бесконечно-малых величин. Общий вопрос обратной задачи
исчисления бесконечно малых состоит в том, чтобы определить одну или
несколько функций одного или нескольких переменных из данных соотно-
шений между независимыми переменными, функциями и их производны-
ми. Пусть имеется ряд независимых переменных:
1, 2, 3, . . .
и ряд функций от этих переменных
1, 2, 3, . . . .
Тогда соотношения, о которых идет
называются дифференциальными уравнениями; порядок наивысшей про-
изводной называется порядком уравнения. Если = 1, то есть независимое
переменное одно, то уравнения называются обыкновенными, если же > 1,
то — уравнениями с частными производными.
Eсли в уравнения входят производные до порядка , то уравнение называ-
ется уравнением -го порядка.
Определение функций из дифференциальных уравнений, или интегри-
рование дифференциальных уравнений, можно понимать различно.
Самая узкая постановка задачи следующая: выразить искомую функ-
цию через элементарные функции. В этом смысле, вообще говоря, задача,
конечно, не всегда разрешима, так как даже для самого простейшего диф-
ференциального уравнения
/= ()
имеем
=() +
и не всегда выражается в элементарных функциях, хотя бы это и имело
место для ().
Во-вторых, нахождение функции, удовлетворяющей дифференциально-
му уравнению, можно понимать в смысле указания приема, которым по
каждому значению переменного находится значение функции. Такие при-емы могут быть весьма разнообразны, например, задача в этом смысле
будет разрешена, коль скоро будет найдено разложение функции в сходя-
щийся ряд, более или менее простого типа. Взяв известное число членов,
для каждого значения переменного в пределах сходимости ряда получим
с любым приближением значение функции.
Третье толкование определения функции из дифференциального урав-
нения состоит в том, что мы считаем задачу разрешенной, как только нам
удастся привести ее к другим более простым задачам, и именно к вычисле-
нию интегралов данных функций, или квадратурам. Таким образом, воз-
никает вопрос о дифференциальных уравнениях, приводимых к квадрату-
рам.
Дифференциальные уравнения
1. Основные понятия
Определение. Уравнение вида
F(x,y,y',y'',…,y(n)) = 0,
связывающее аргумент х, функцию у(х) и ее производные, называется дифференциальным уравнением n-го порядка.
Определение. Общим решением дифференциального уравнения n-го порядка называется функция у = (х, С1,С2,…,Сn), которая зависит от аргумента х и n независимых произвольных постоянных С1, С2, …, Сn, обращающая вместе со своими производными у', у'',…, у(n) уравнение в тождество.
Определение. Частным решением уравнения называется решение, которое получается из общего решения, если придавать постоянным С1, С2, …, Сn определенные числовые значения.
Линейные дифференциальные уравнения первого порядка
Определение. Уравнение вида y'+(x)y=f(x), где (x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
Пример. Найти общее решение уравнения y'+3y=e2x и частное решение,удовлетворяющее начальным условиям х=0, у=1.
Решение. Данное уравнение является линейным.
Здесь (x)=3 и f(x)=e2x.
Решение ищем в виде y=U, где U и – некоторые функции от х. Находим y'= U'+ U' и подставляем в уравнение значение y и y', получаем: U'+U'+3U=e2 x или U'+U('+3)= e2x.
Найдем одно значение , при котором выражение в скобках, обращается в нуль: '+3=0. Получим уравнение с разделяющимися переменными. Решая его получаем: 
 ln =–3x,=e–3x.
ln =–3x,=e–3x.
Подставляем найденное значение в исходное дифференциальное уравнение, получаем уравнение с разделяющимися переменными:
 .
.
Итак, общее решение данного уравнения имеет вид:
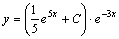 . 2
. 2
Найдем частное решение. Для этого подставим начальные условия в выражение для общего решения и найдем С.
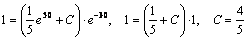 .
.
Частное решение имеет вид:  .
.