Класифікація та властивості похибок вимірів

Результати високоточних вимірів не співпадають з істинними значеннями вимірюваних величин, а повторні вимірювання не дають однакові результати. Це виникає тому, що в кожному вимірюванні неможливо абсолютно точно дотриматись незмінності комплексу умов. Тобто кожен результат вимірів обмежений похибками вимірювань.

Різницю між результатом вимірювань х і істинною величиною Х, або дійсною величиною 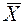називають похибкою вимірів:

D = х – Х; 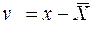. (4.2)

За своїм характером похибки діляться на:

Грубі похибки – величина яких недопустима при даному комплексі умов. Їх виявляють шляхом обчислень і такі результати в математичну обробку не включають, а вимірювання повторюють.

Систематичні похибки – похибки, які входять в кожен результат вимірів з одним знаком, однією величиною або змінюються за певним законом (функцією). Величину їх визначають шляхом експериментальних вимірювань і вводять в результати вимірів.

Якщо відомі істинне значення Х та дійсне значення 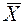, то систематичну похибку визначають за формулою:

(4.3)

де с, l – систематична похибка.

Випадкові похибки виникають внаслідок незначного порушення комплексу умов при кожному вимірюванні, причому їх величину і знак передбачити неможливо.

Випадкові похибки в свою чергу поділяють на:

- істинні D_і = х_і - Х ; (4.4)

- імовірні v_i = x_i - 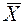, (4.5)

де Х – істинне значення шуканої величини;

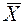– дійсне, імовірне або середнє арифметичне значення вимірюваної величини;

х_і – результат вимірювання.

Імовірним значенням називають отримане за результатами обробки вимірів х₁, х₂, ..., х_п значення шуканої величини найбільш близьке до істинного.

Вивченням властивостей та закономірності дії похибок вимірів, розробкою методів отримання найбільш точних значень виміряних величин та характеристик їх точності займається теорія похибок вимірів.

Випадкові істинні та імовірні похибки при заданому комплексі умов мають такі властивості.

1. Обмеженості. По абсолютній величині не перевищують граничної величини

|D| £ D_гр. (4.6)

2. Унімодальності. Малі по абсолютній величині випадкові похибки зустрічаються в ряду вимірів х₁, х₂, ..., х_п частіше великих

N_D_min ³ N_D_max . (4.7)

3. Симетричності. В достатньо великому ряду вимірів кількість похибок з різними знаками приблизно однакова

N₍₊_D₎ » N_(-_D₎. (4.8)

4. Компенсації. Сума випадкових похибок розділена на їх число, при необмеженій кількості вимірів наближається до нуля

. (4.9)

Властивість компенсації випадкових похибок дозволяє визначити по ряду вимірів однієї і тієї ж величини результат, найбільш близький до істинного.

3. Математична обробка рівноточних вимірів

Виконано ряд вимірів х₁, х₂, ..., х_п при практично незмінному комплексі умов. Тоді вимірі х_і вважаються рівноточними [8].

Обчислимо істинні похибки за формулою 4.4, складемо їх, поділимо на п і отримаємо:

; (4.10)

___________

. (4.11)

За четвертою властивістю при n ®¥ .

Тоді . (4.12)

Позначимо і отримаємо 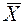= Х, коли n ®¥. Це означає, що при достатньо великій кількості вимірів, середнє арифметичне 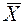буде найбільш імовірним значенням, тобто найбільш близьким до істинного значення Х. Таку властивість називають принципом арифметичної середини.

Таким чином визначена кількісна характеристика вимірів, середнє арифметичне або ймовірне значення обчислюється за формулою

, (4.13)

або , (4.14)

Критерієм(мірою) точності, або якісними характеристиками ряду вимірів є середні квадратичні похибки:

а) кожного окремого виміру х_і:

- за формулою Гаусса

, (4.15)

застосовується коли відоме істинне значення шуканої величини;

- за формулою Бесселя

, (4.16)

застосовується коли невідоме Х, а обчислене .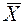

б) середнього арифметичного

. (4.17)

Допустима (гранична) похибка в ряду вимірів х₁, х₂, ..., х_п обчислюється за формулою

D_гр = ±t×m, (4.19)

де параметр t обчислюється або вибирається із таблиці функції Лапласса в залежності від заданої довірчої ймовірності р. Відповідно маємо:

р = 0,997 t = 3,0 – при високоточних вимірюваннях;

р = 0,95 t = 2,5 – при вимірюваннях середньої точності;

р = 0,90 t = 2,0 – при технічних вимірюваннях.

Систематичну похибку обчислюють за формулою:

, або . (4.20)

Якщо в ряду вимірів |D_і| > D_гр або |v_i| > D_гр, то такий вимір вважається грубим, його відкидають і його вимірювання повторюють.

Для лінійних вимірювань визначають відносні похибки, які теж є мірою точності:

- відносна середня квадратична похибка

; (4.21)

- відносна гранична похибка

; (4.22)

На основі отриманих характеристик , m, M, D_гр та роблять остаточний висновок про якість вимірів.

Таблиця 4.1

№ виміру	х_і(м)	v_i (см)	Обчислення
	181,32	+6	= 181,26 м
	181,21	- 5	= 4,7 см
	181,24	- 2	= 2,35 см
	181,27	+1	D_гр = ± 2× 4,7 = ± 9,4 см
S	625,04		1/Т = 9,4/181,26 = 1/1928

Оскільки v_i < D_гр, то вимірювання виконані правильно без грубих помилок.

4. Математична обробка нерівноточних вимірів

В ряду нерівноточних вимірів х₁, х₂, ..., х_п будемо мати різні оцінки точності, тобто .

За спеціальну міру відносної точності в ряду нерівноточних вимірів приймають коефіцієнт або вагу р_і, яка обчислюється за формулою

; ; , або , (4.23)

де С – умовно прийнятий постійний коефіцієнт з таким значенням, щоб ваги р_і в ряду вимірів були близькі до одиниці;

В ряду вимірів ваги P_i можна пропорційно збільшити або зменшити в 10 ± n.

m_i – середня квадратична похибка окремого виміру;

L_i – довжина вимірюваної величини;

N_i – число вимірювань, шуканої величини величини;

п_і – число вимірів окремих величин х_і.

Для ряду нерівноточно виміряної величини Х ймовірним або найближчим значенням (найбільш точним) буде загальне середнє арифметичне .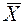

, (4.24)

або , (4.25)

де х_і – результати вимірів;

р_і – ваги вимірів обчислені за однією із формул (4.23).

Мірами або критерієм точності нерівноточних вимірів приймають:

а) середня квадратична похибка (СКП) одиниці ваги або СКП того виміру, вага якого дорівнює одиниці (р_і = 1)

- за формулою Гаусса

, (4.26)

- за формулою Бесселя

, (4.27)

де D_і, v_i – випадкові похибки, які обчислюються за формулами (4.4; 4.5).

б) середня квадратична похибка загального середнього арифметичного

; (4.28)

в) середні квадратичні похибки окремих вимірів

. (4.29)

Систематичну похибку обчислюють за формулою

, або . (4.30)

Гранична похибка за окремим завданням обчислюється для заданого або кожного виміру за формулою

. (4.31)

Приклад визначення висоти точки місцевості А (рис.4.2) від чотирьох вихідних реперів наведено в табл. 4.2.

Таблиця 4.2

№ ходу Н_А (м) L (км) р = DН = Н_і – Н₀ (см) рDН V cм pv pv²

204,36 1,0 +14 +14 -2 -2 4,0

204,22 0,6 -16 -9,6 153,6

204,46 1,7 +24 +40,8 +8 +13,6 108,8

204,35 0,8 +13 10,4 -3 -2,4 7,2

H₀ 204,22 S 4,1 S +65,2 S -0,4 273,6

Рис. 4.2. Схема визначення висоти точки А

Вага р при С = 10 обчислені за формулою (4.23).

Загальне середнє арифметичне обчислене за формулою

,

де Н₀ – мінімальне значення із отриманих висот по ходу 2.

Середні квадратичні похибки одиниці ваги m та загального середнього арифметичного дорівнюють:

9,5 см; 4,6 cм.

Середня квадратична похибка визначення висоти точки А по третьому ходу складе

7,3 см.

5. Оцінка точності функцій виміряних величин

При виконанні посередніх вимірів безпосередньо вимірюють декілька величин х₁,х₂,...,х_п. Шукана величина обчислюється за функцією

у = f(х₁, х₂, ..., х_п). (4.32)

Рис. 4.3. Схема визначення недоступної відстані

Тоді шукану відстань визначають за формулою

L_AB = bctgg. (4.33)

Якщо відомі середні квадратичні похибки m₁, m₂, ..., m_п безпосередньо виміряних величин х₁, х₂, ..., х_п для визначення функції у (формула 4.32), то середня квадратична похибка функції m_y буде дорівнювати корню квадратному із суми квадратів добутку часткових похідних функцій по кожному із аргументів на середні квадратичні похибки відповідних

аргументів , тобто

, (4.34)

де - часткові похідні функції у по наближеним (виміряним) значенням аргументів х_і.

Для функції у = х₁ ± х₂ ± ... ± х_п =

отримаємо

(4.35)

Для функції у = с₁х₁ ± с₂х₂ ± ... ±с_nх_п =

Тоді

(4.36)

Приклад. При визначені на місцевості площі S прямокутної ділянки виміряні сторонами а = 40м та b = 20 м з середніми квадратичними похибками m_a = 2 см ; m_b = 1см.

Розв’язання. Площа ділянки обчислюється за формулою S = a × b.

За формулою (4.34) визначимо середню квадратичну похибку площі ділянки

оскільки ; ,

Тоді .