Карты Карно. Диаграммы Вейча

Минимизировать нормальные формы можно различными способами. Одним

из таких методов являются карты Карно для ДНФ и диаграммы Вейча для КНФ.

Минимальная или сокращенная нормальная форма получается из совершенной дизъюнктивной (конъюнктивной) нормальной формы удалением некоторых элементарных конъюнкций (дизъюнкций).

Тупиковой нормальной формой называется ДНФ(КНФ), из которой уже нельзя

удалить ни одной элементарной конъюнкции (дизъюнкции) так, чтобы сохранить неизменной заданную булеву функцию.

Для представления булевой функции в таком виде необходимо сначала представить ее в совершенной форме, а только затем минимизировать до тупиковой формы. Карты Карно являются одним из наиболее удобных способов минимизации. Они впервые появились в одной из статей Мориса Карно в 1953г. Это специальные таблицы, дающие возможность упростить процесс поиска минимальной формы булева выражения с помощью графического представления для 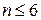. Они имеют вид прямоугольника, разделенного на клеток, в каждой из которых двоичный -мерный набор значений функции из таблицы истинности.

Для карта Карно имеет вид таблицы, состоящей из клеток.

			или

Логическая функция на карте Карно представлена совокупностью клеток, заполненных единицами или пустотами – нулями, если известна ее таблица истинности или СДНФ. Единицы соответствуют минтермам.

При карта Карно имеет вид таблицы из клеток,

					или

а для карта Карно представляет собой таблицу из клеток

					или

При заполнении карт Карно необходимо, чтобы каждые две соседние клетки отличались лишь значением одной переменной.

Для построения минимальной ДНФ производится «склеивание» единиц. Скле-иваются только соседние клетки, которые отличаются значением одной переменной.

Процесс сводится к объединению в группы единичных клеток карт Карно. При этом общие переменные сохраняются, а различные опускаются.

Алгоритм «склеивания» при помощи карт Карно имеет следующий вид:

1. Привести булеву функцию к ДНФ или СДНФ.

2. Нанести единицы на карту Карно.

3. Объединить соседние единицы контурами, охватывающими

клеток. При этом может оказаться, что единица попадает одновременно в два контура. Если контур охватывает более одной пары единиц одновременно, то предпочтительнее его не дробить на пары, а рассматривать как единый целый контур, например квадрат.

4. Провести упрощения, т.е. исключить члены, дополняющие друг друга до 1 внутри контура, следя за тем, чтобы переменные внутри контура были связаны операцией конъюнкции.

5. Объединить оставшиеся члены оставшиеся члены (по одному в каждом контуре) функцией ИЛИ, т.е. дизъюнкцией.

6. Записать полученное упрощенное булево выражение в ДНФ.

Пример. Минимизировать булеву функцию при помощи карты Карно

.

Решение. Нанесем единицы на карту Карно

и обведем их вначале попарно двумя вертикальными контурами (можно и горизонтальными). Это действие соответствует группировке слагаемых и . Вынесем теперь за скобки одинаковые конъюнкции. Получим

; .

Как видно, объединение двух соседних единиц всегда приводит нас к закону исключенного третьего для одной переменной. Поэтому при записи ответа после применения карты Карно переменные, заключенные в общий контур, связываются

конъюнкцией, а такие отдельные конъюнкции, т.е. различные контуры, объединяются между собой дизъюнкцией. Тогда .

Однако в этом примере удобнее рассмотреть целиком весь квадрат из четырех

единиц и сравнить переменные, записанные в вертикальных и горизонтальных клет-

ках. Очевидно, что после упрощения общие множители сохранятся, а инвертируе-

мые уйдут. Поэтому целесообразно сразу опустить инвертируемые пары и

, а в ответе сохранить общую для всех клеток переменную .

Семантический способ минимизации (применение эквивалентных преобразований) дает тот же самый результат:

Пример. Минимизировать булеву функцию четырех переменных

.

Решение. Построим карту Карно

Рассмотрим переменные, заключенные контуром в квадрат. Среди них есть повторяющиеся в соседних клетках (это и ) и инвертируемые (это пары , и , ). Повторяющиеся переменные мы сохраним, а инвертируемые опустим. Из контура, содержащего две единицы, вынесем переменные и , расположенные в одной строке, а также одинаковую для первых двух столбцов переменную и при этом опустим инвертируемую пару , . После этих преобразований булева функция примет вид . Используя эквивалентные преобразования можно получить тот же самый результат.

Пример. Минимизировать булеву функцию четырех переменных

еременные, заключенные контуром в квадрат. ет тот же самый результат:

ах.. третьего для одной переменной.

Решение. Построим карту Карно. Отметим, что чередование переменных в строке и столбце ничем не ограничено. Такой порядок был введен для удобства последующего упрощения. Поэтому можно сделать так, чтобы все единицы в данном случае оказались рядом.

Для этого достаточно «склеить» крайний левый и правый столбцы. Фактичес-

ки это соответствует свертыванию карты в вертикальный цилиндр, в котором левый край совмещается с правым. При их совмещении единицы первого и последнего

столбцов окажутся в одном контуре и к ним можно применить алгоритм склеивания.

Таким образом, и без мысленного сворачивания карты можно циклически переставлять аргументы в строках и столбцах. Из всей четверки единиц по вертикали сохранится общая переменная второй и третьей строк , а по горизонтали общая переменная первого и последнего столбцов . Переменные, находящиеся в одном контуре соединяем знаком конъюнкции: .

Пример. Минимизировать булеву функцию четырех переменных

.

Решение. Строим карту Карно. еременные, заключенные контуром в квадрат. ет тот же самый результат:

ах.. третьего для одной переменной.

Здесь удобно переставить переменные в столбце, что соответствует свертыванию карты в горизонтальный цилиндр так, чтобы совместились верхние и нижние края, и образовался квадрат. В первой и последней строках сохраняется общая переменная , а в первом и втором столбцах общая переменная . Их конъюнкция и является ответом: .

Пример. Минимизировать булеву функцию четырех переменных

.

Решение. Нанесем единицы на карту.

Ясно, что подобную карту надо «свернуть в шар» и одновременно склеить четыре единицы, расположенные по углам. Для полученного квадрата вновь применим тот же алгоритм, сохранив переменные, одинаковые для первой и последней строк , а также первого и последнего столбцов : .

Проверим правильность вычислений.

Пример. Минимизировать функцию .

Решение. Объединим единицы в контуры по два элемента. Получилось два

контура, один из которых дает , а второй . Тогда упрощенный вариант булевой функции содержит дизъюнкцию этих переменных.

Попадание единицы в два и более контура соответствует закону идемпотентности , поэтому каждое слагаемое (элементарная конъюнкция) может быть представлено столько раз, сколько требуется для упрощения. При этом они группируются с другими слагаемыми, с которыми попали в один контур, независимо.

Ответы совпали, что подтверждает правильность преобразований.

Пример. Минимизировать функцию трех переменных

.

Решение. Составим карту Карно. Объединим контурами полученные единицы.

Опустим дополняющие друг друга переменные: и . Тогда

.

Проверка.

Пример. Минимизировать функцию

.

Решение. Строим карту Карно

Убираем инвертируемые переменные в квадрате и . Получим общую переменную . Рассмотрим теперь единицы, попавшие в контур на пересечении 1, 2 столбца и первой строки. Уберем инвертируемую пару и получим . Объединим полученные результаты дизъюнкцией и получим упрощенную

формулу .

Пример. Упростите булеву функцию .

Заполним таблицу истинности данной функции и построим СДНФ.

СДНФ булевой функции имеет вид .

Строим карту Карно

Объединяем пары единиц в контуры и получаем .

Для минимизации булевой функции на множестве КНФ используются диаграммы Вейча. Их построение аналогично картам Карно. На карте обозначаются клетки, которые отвечают нулевым интерпретациям. После этого производится склеивание клеток, которые содержат нули и формирование минимальной КНФ. Склеивание клеток осуществляется по тем же правилам, что и при дизъюнктивной минимизации. Каждая группа клеток, полученная при склеивании, отвечает дизъюнкции только тех переменных, которые имеют одинаковые значения для всех клеток группы. Переменные берутся без отрицания, если им отвечает нулевое значение, и с отрицанием в противном случае. Конъюнкция полученных элементарных дизъюнкций есть результат минимизации формулы.

Пример. Минимизировать функцию

.

Решение. Вычислим значения функции на все восьми наборах, выберем нулевые интерпретации и нанесем их на карту. Тогда

 

х|yz

Упрощенный вариант булевой функции имеет вид

.

Проверка.