Натуральное число как мера величины

Понятие целого неотрицательного числа

Теоретико-множественный смысл целых неотрицательных чисел

Позиционные и непозиционные системы счисления. Особенности десятичной системы счисления. Запись числа в десятичной системе счисления.

4.Сравнение натуральных чисел.

Разбор натурального числа.

6. Римская нумерация

Позиционные системы счисления, отличные от десятичной

Теоретико-множественный смысл целых неотрицательных чисел

Терминологический минимум:отрезок натурального ряда N_а; конечное множество; счет элементов множества; теоретико-множественный смысл натурального числа; теоретико – множественный смысл отношений “равно” и “меньше”.

Количественные натуральные числа. Счет. Отрезком натурального ряда N_а натурального ряда называется множество натуральных чисел, не превосходящих числа а. N_а = { х\ х ÎN, х £ а }. Свойства отрезков натурального ряда:

Любой отрезок N_асодержит единицу.
Если число х содержится в отрезке N_а и х ¹а , то и непосредственно следующее за ним число х+1 также содержится в N_а.

Множество А называется конечным, если оно равномощно некоторому отрезку N_а натурального ряда. Если непустое конечное множество А равномощно отрезку N_а , то натуральное число а называют числом элементов множества А и пишут n(А) = а. Счетом элементов множества А называется установление взаимно – однозначного соответствия между элементами непустого конечного множества А и отрезком натурального ряда N_а. Счет бываетколичественными порядковым. Задание 1. Что значит «пересчитать» элементы конечного множества? Задание 2. Сформулируйте условия, которые должны соблюдать учащиеся, ведя количественныйсчет предметов. Задание 3.Сформулируйте условия, которые должны соблюдать учащиеся, ведя порядковыйсчет предметов. Задание 4.Что общего и чем отличаются количественный и порядковый счет?

Теоретико - множественный смысл натурального числа и нуля. Любому непустому конечному множеству соответствует только одно натуральное число, значит вся совокупность конечных множеств разбивается на классы равномощных множеств. В одном классе будут содержаться все одноэлементные множества, в другом все двухэлементные, и т.д. Множества одного класса различны по своей природе, но все они содержат одинаковое число элементов. И это число можно рассматривать как общее свойство класса конечных равномощных множеств. Т.о. натуральное число – это общее свойство класса конечных равномощных множеств. Нуль– общее свойство класса пустых множеств. 0 = n ( Æ ). Натуральное число а, как характеристику множества можно рассматривать с двух позиций: 1.Как число элементов в множестве А, получаемое при счете, т. е. n(А) = а и А~ N_а. 2.Как общее свойство класса конечных равномощных множеств.

Контрольные вопросы и задания. 1. Прочитайте предложения n(А) =3, n(B)=5. В какой роли здесь выступает натуральное число? 2. Из школьных учебников математики для начальных классов приведите примеры двух заданий, в которых число выступает как: а) порядковое число; б) количественное число.

Натуральное число как мера величины

Известно, что числа возникли из потребности счета и измерения, но если для счета достаточно натуральных чисел, то для измерения величин нужны и другие числа. Однако в качестве результата измерения величин будем рассматривать пока только натуральные числа. Определив смысл натурального числа как меры величины, мы выясним, какой смысл имеют арифметические действия над такими числами. Эти знания нужны учителю начальных классов не только для обоснования выбора действий при решении задач с величинами, но и для понимания еще одного подхода к трактовке натурального числа, существующего в начальном обучении математике. Натуральное число мы будем рассматривать в связи с измерением положительных скалярных величин-длин, площадей, масс, времени и др. Поэтому, прежде чем говорить о взаимосвязи величин и натуральных чисел, напомним некоторые факты, связанные с величиной и ее измерением, тем более, что понятие величины, наряду с числом, является основным в начальном курсе математики.

Понятие положительной скалярной величины и ее измерения Величины – это особые свойства реальных предметов и явлений. Например, свойство предметов иметь протяженность называется длиной. Это же слово мы употребляем, когда говорим о протяженности конкретных объектов. Поэтому про длины конкретных объектов говорят, что величины одного рода. Разнородные величины выражают различные свойства объектов. Величины бывают скалярными и векторными. Скалярные величины характеризуются только числом, а векторные числом и направлением. Свойства однородных величин. 1.Любые две величины одного рода сравнимы. Т.е. для однородных величин а и b справедливо одно из отношений: а á b, а = b или а ñ b. 2.Величины одного рода можно складывать ( вычитать), в результате получится величина того же рода. 3. Величины одного рода можно вычитать, в результате получится величина того же рода. 4.Величину умножают на действительное число, получая в результате величину того же рода. 5.Величины одного рода делят, получая в частном действительное число.

Понятие измерения величины Сравнивая величины непосредственно, мы можем установить их равенство или неравенство. Чтобы получить более точный результат сравнения, например, узнать, на сколько одна величина больше другой, необходимо величины измерить. Измерение заключается в сравнении данной величины с некоторой величиной того же рода, принятой за единицу. Если дана величина а и выбрана единица величины e, то в результате измерения величины а находят такое действительное число х, что а = х×e. Это число х называют численным значением величины апри единице величины е. Последнее предложение можно записать в символической форме: х = m_e(a). Измерение величин позволяет свести сравнение их к сравнению чисел, операции над величинами к соответствующим операциям над числами. 1. а = b Û m_e(a) = m_e(b). 2. а + b =c Û m_e(a) + m_e(b) = m_e(c). 3. b =x ×a Û m_e(b) = x ×m_e(a).

Смысл натурального числа, полученного в результате измерения величины. Выясняя смысл натурального числа как меры величины, все рассуждения будем вести на примере одной величины-длины отрезка. Определение. Если отрезок х состоит из а отрезков, каждый из которых равен единичному отрезку е, т. Число а называют численным значением длины Х данного отрезка при единице длины Е. Пишут: Х=а·Е. Из данного определения получаем, что натуральное число как результат измерения длины отрезка (или как мера длины отрезка) показывает, из скольких единичных отрезков состоит отрезок, длина которого измеряется.

Даны отрезки:

с Задание. Измерьте длину отрезка с отрезком а. Измерьте длину отрезка с отрезком в. Запишите результаты измерения. Что заметили? Как это объяснить? При выбранной единице длины Е это число единственное. В связи с таким подходом к натуральному числу сделаем два замечания: 1) При переходе к другой единице длины численное значение длины заданного отрезка изменяется, хотя сам отрезок остается неизменным. 2) Если отрезок х состоит из а отрезков, равных е, а отрезок у-из b отрезков, равных е, то а= b тогда и только тогда, когда отрезки х и у равны.

Контрольные вопросы и задания 1. При измерении различных величин получились следующие результаты: 3 дм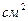; 3

; 3

; 3л; 3га; 3ч. Какие величины измеряли? Что в каждом из этих случаев показывает число 3? 2. При каких условиях натуральное число n называют мерой отрезка а? 3. Как изменится численное значение массы при уменьшении единицы в 16 раз? 4. Как изменится численное значение площади при увеличении единицы площади в 100 раз? 5. Как изменится численное значение объема при переводе кубических метров в литры? 6. Как изменится численное значение времени при переводе суток в часы. 7. Как изменится численное значение массы при переводе тонны в граммы. 8. Как изменится численное значение площади при переводе квадратных метров в квадратные километры? 9. Измерив два отрезка, некоторой единицей длины, получили, что один из них длиннее другого в 2 раза. После этого единицу длины уменьшили в 10 раз. Изменится ли результат сравнения длин отрезков?

3.Позиционные и непозиционные системы счисления.Особенности десятичной системы счисления. Запись числа в десятичной системе счисления

Еще до появления письменности люд умели называть числа, вести счет. Вести счет помогали разные приспособления. И, прежде всего, пальцы рук и ног. И даже в наше время используется эта «счетная машина»: дети, начиная учиться, часто пользуются при счете своими пальцами. Издревле, при счете употреблялись деревянные палочки с зарубками, шнуры и веревки с узлами. Способ «записи» при помощи зарубок и узлов был не слишком удобен, поскольку для записи больших чисел приходилось делать много зарубок или узлов. Такие числа трудно было сравнивать друг с другом, трудно было выполнять действия над ними. Поэтому возникли иные, более экономные способы записи чисел: счет стали вести группами, состоящими из одинакового числа элементов – из 5, 10, 12,20 элементов. Так, счет двадцатками использовали люди племени майя. В Древнем Вавилоне считали группами по 60 единиц. Например, число 185 представлялось как 3 раза по 60 и еще 5. Записывалось такое число с помощью двух знаков, один из которых обозначал, сколько раз взято по 60, а другой – сколько взято единиц. Древневавилонскую систему мя используем и в настоящее время при отсчете времени и углов в минутах и секундах.

Язык для наименования, записи чисел и выполнения действий над ними называется системой счисления. Системы счисления бывают:

Позиционные	непозиционные
В позиционных системах счисления один и тот же знак может иметь разное значение в зависимости от места (позиции) этого знака в записи числа.	В непозиционных системах счисления знак не меняет своего значения в зависимости от его места в записи числа
-десятичная, -вавилонская шестидесятиричная	- римская, -славянская, -греческая ( ионическая).
	MMDV