Механические гармонические колебания – математический и физический маятники, пружинный маятник.
Пусть материальная точка совершает гармонические колебания вдоль оси x около положения равновесия, задаваемые уравнением вида:
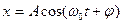 .
.
Сила, действующая на колеблющуюся материальную точку, в соответствии с уравнением 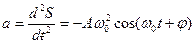 равна:
равна:
 .
.
Из него следует, что действующая сила пропорциональна смещению и направлена в противоположную сторону, т.е. к положению равновесия.
Кинетическая энергия колеблющейся точки:
 .
.
Потенциальная энергия:
 .
.
Полная механическая энергия равна сумме кинетической и потенциальной:
 .
.
Из данного уравнения следует, что полная энергия при гармонических колебаниях с течением времени не изменяется, что соответственно закону сохранения механической энергии этот результат становится понятным, если учесть, что упругие силы консервативны.
Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида:  (1).
(1).
Примерами гармонических осцилляторов являются физический, математический и пружинный маятники, а так же колебательный контур.
1) Пружинный маятник – это груз, массой m, подвешенный на абсолютно упругой пружине и совершающий колебания под действием упругой силы:  .
.
В соответствие со 2-м законом Ньютона:  ;
;  .
.
Из последнего уравнения следует, что пружинный маятник совершает гармонические колебания:
 , с циклической частотой
, с циклической частотой  и периодом
и периодом  (2).
(2).
Формула (2) справедлива для случая упругих колебаний, при этом потенциальная энергия пружинного маятника:  .
.
2) Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс.
 В соответствием с основным уравнением динамики вращательного движения:
В соответствием с основным уравнением динамики вращательного движения:  .
.
Поскольку речь идет о малых колебаниях: 
 .
.
Следовательно физический маятник совершает гармонические колебания по закону:  . С циклической частотой:
. С циклической частотой:  . С периодом колебаний
. С периодом колебаний  .
.
 - приведенная длина физического маятника.
- приведенная длина физического маятника.
Точка  на продолжении прямой OC и отстоящая от оси подвеса на расстоянии приведенной длины L называется центром качаний физического маятника.
на продолжении прямой OC и отстоящая от оси подвеса на расстоянии приведенной длины L называется центром качаний физического маятника.
Точка подвеса O и центр качаний  обладают свойством взаимозаменяемости.
обладают свойством взаимозаменяемости.
3) Математический маятник – это идеализированная система, состоящая из материальной точки массой m, подвешенная на нерастяжимой, невесомой нити и совершает колебания, под действием силы тяжести.
Математический маятник является частным случаем физического маятника с моментом инерции  . Подставив значение момента инерции в формулу для периода колебаний физического маятника получим
. Подставив значение момента инерции в формулу для периода колебаний физического маятника получим  .
.
Из последней формулы вытекает следующее определение приведенной длины физического маятника. Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.