Методические указания к решению задач
Содержание
| 1. | Порядок выполнения контрольной работы | |
| 2. | Программа курса | |
| 3. | Список рекомендуемой литературы | |
| Задание 1 | ||
| Задание 2 | ||
| Задание 3 | ||
| Задание 4 | ||
| Задание 5 | ||
| Задание 6 | ||
| Задание 7 | ||
| Задание 8 | ||
| Задание 9 | ||
| 4. | Методические указания к решению задач | |
| 5. | Приложение |
Порядок выполнения контрольной работы
Контрольная работа для студентов заочной формы обучения включает 9 задач. Студент по последней цифре номера зачетной книжки выбирает нужный вариант (если номер заканчивается цифрой 0, то выполняется 10 вариант).
При выполнении контрольной работы необходимо строго придерживаться указанных ниже правил. Работы, выполненные с нарушением правил, не засчитываются и возвращаются для переработки.
1. Контрольная работа должна быть выполнена в отдельной тетради, на внешней обложке которой должны быть указаны:
а) контрольная работа по курсу «Теория вероятностей и математическая статистика»;
б) фамилия и инициалы студента, номер варианта;
в) название специальности, курса, группы;
г) фамилия преподавателя.
Решения всех задач и пояснения к ним должны быть достаточно подробными. Для замечаний преподавателя необходимо на каждой странице оставлять поля.
2. Решение задач следует располагать в порядке возрастания их номеров.
3. Перед решением каждой задачи необходимо полностью выписать ее условие, заменив буквенные обозначения числовыми данными, соответствующими своему варианту.
4. Работа должна быть подписана студентом. Контрольная работа должна быть сдана на проверку за 10 дней до начала сессии.
Программа курса
Раздел I. Теория вероятностей
Классификация событий и правила действия с ними. Классическое, статистическое и геометрическое определение вероятности случайного события. Основные теоремы сложения и умножения вероятностей. Формула полной вероятности. Формула Байеса.
Схема независимых повторных испытаний Бернулли. Формула Бернулли. Локальная и интегральная теорема Муавра-Лапласа.
Понятие случайной величины. Закон распределения вероятностей дискретной случайной величины. Функция распределения. Непрерывная случайная величина. Плотность вероятностей. Числовые характеристики системы случайных величин. Примеры распределений: биномиальное, Пуассона, гипергеометрическое, равномерное, показательное и нормальное распределения.
Понятие функции случайных величин. Числовые характеристики функции случайных величин. Неравенства Маркова и Чебышева. Теорема Чебышева и теорема Бернулли. Понятие о законе больших чисел и центральной предельной теореме.
Раздел 2. Математическая статистика
Генеральная совокупность и выборка. Статистическое распределение выборки. Полигон и гистограмма частот. Выборочная функция распределения.
Выборочные моменты. Оценка и ее свойства. Методы нахождения точечных оценок. Интервальное оценивание параметров генеральной совокупности (математического ожидания, дисперсии и вероятности).
Статистическая гипотеза. Статистический критерий. Ошибки первого и второго рода. Критическая область. Проверка гипотезы о математическом ожидании и дисперсии. Проверка гипотезы о виде распределения (критерий Пирсона).
Корреляционная зависимость. Корреляционная таблица. Выборочный парный коэффициент корреляции, его свойства и экономическая интерпретация. Проверка значимости коэффициента корреляции. Коэффициент детерминации и его экономическая интерпретация. Матрица парных и частных коэффициентов корреляции. Множественная корреляция.
Простая регрессия. Оценивание параметров уравнения регрессии методом наименьших квадратов. Проверка гипотезы о значимости параметров уравнения регрессии. Множественная линейная регрессия. Понятие о нелинейной регрессии.
Список рекомендуемой литературы
1. Белько И.В., Кузьмич К.К. Высшая математика для экономистов (III семестр). – М.: ООО «Новое знание», 2002 г.
2. Белько И.В., Свирид Г.П. Теория вероятностей и математическая статистика. Примеры и задачи. – М.: ООО «Новое знание», 2002 г.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979 г.
4. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2001 г.
5. Гурский Е.И. Сборник задач по теории вероятностей и математической статистике. – Мн.: Вышэйшая школа, 1984 г.
6. Малыхин В.И. Математика в экономике: учебное пособие. – М.: ИНФРА-М, 2001 г.
Задание 1
| Варианты 1-4 | Из N вопросов программы студент подготовил М вопросов. Зачет считается сданным, если студент ответит не менее чем на k из n поставленных в билете вопросов. Какова вероятность того, что студент сдаст зачет? |
| Вариант 1: N = 30; М = 25; k = 2; n =3. Вариант 2: N = 35; М = 30; k = 3; n =5. Вариант 3: N = 25; М = 20; k = 1; n =3. Вариант 4: N = 40; М = 30; k = 2; n =4. | |
| Варианты 5-8 | Партия изделий состоит из K изделий первого сорта, L изделий второго сорта и М изделий третьего сорта. Какова вероятность того, что из n отобранных случайным образом изделий k изделий первого сорта, l изделий второго сорта и m изделий третьего сорта? |
Вариант 5: K = 35; L = 10; М = 5; n =3; k 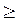 2.
Вариант 6: K = 30; L = 6; М = 4; n =3; l 2.
Вариант 6: K = 30; L = 6; М = 4; n =3; l 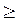 2.
Вариант 7: K = 40; L = 7; М = 3; n =2; m 2.
Вариант 7: K = 40; L = 7; М = 3; n =2; m 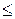 1.
Вариант 8: K = 25; L = 8; М = 2; n =2; l 1.
Вариант 8: K = 25; L = 8; М = 2; n =2; l 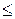 1. 1.
| |
| Варианты 9-10 | На полке имеется N тетрадей, из которых M в линейку, остальные в клетку. Найти вероятность того, что при случайном изымании n тетрадей k из них будет в линейку. |
Вариант 9: N = 15; М = 4; n = 3; k 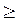 2.
Вариант 10: N = 14; М = 7; n = 5; k 2.
Вариант 10: N = 14; М = 7; n = 5; k 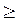 4. 4.
|
Задание 2
| Вариант 1 | Агрегат, имеющий 3 узла способен функционировать, если работает не менее 2 из них. Вероятность выхода из строя первого узла равна 0,015; второго – 0,01; третьего – 0,025. Какова вероятность выйти из строя агрегату? |
| Варианты 2-4 | Для проверки на морозоустойчивость различных сортов яблони высажено 3 саженца. Вероятность выдержать испытание для первого саженца равна 0,9, для второго 0,95, для третьего 0,85. Какова вероятность того, что выдержат испытание: |
| Вариант 2: не менее двух саженцев. Вариант 3: не более одного саженца. Вариант 4: хотя бы один из саженцев. | |
| Вариант 5 | Машинистка печатает корреспонденцию. Вероятность допустить ошибку при наборе страницы текста равна 0,25. Найти вероятность того, что четыре страниц текста набраны без ошибок. |
| Варианты 6–10 | Рабочий обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,85, второй – 0,9; третий – 0,75; четвертый – 0,8. Какова вероятность того, что в течение часа: |
| Вариант 6: ни один станок не потребует внимания. Вариант 7: все четыре станка потребуют внимания. Вариант 8: хотя бы один станок потребует внимания. Вариант 9: только один станок потребует внимания. Вариант 10: только два станка потребуют внимания. |
Задание 3
| Варианты 1-4 | В ящике имеется N деталей. Из них n1 изготовлено на первом станке, n2 – на втором, остальные – на третьем. Вероятность изготовления стандартной детали на первом станке равна р1, на втором станке – р2, на третьем станке – р3. Случайно выбранная деталь оказалась бракованной. Найти вероятность того, что она изготовлена на i-м станке. |
| Вариант 1: N = 30; n1 = 8; n2 = 10; р1 = 0,9; р2 = 0,92; р3 = 0,94; i = 3. Вариант 2: N = 25; n1 = 7; n2 = 12; р1 = 0,95; р2 = 0,91; р3 = 0,9; i = 2. Вариант 3: N = 35; n1 = 10; n2 = 14; р1 = 0,93; р2 = 0,9; р3 = 0,96; i = 3. Вариант 4: N = 40; n1 = 15; n2 = 12; р1 = 0,92; р2 = 0,96; р3 = 0,91; i = 1. | |
| Варианты 5-8 | В торговую фирму поступили холодильники от трех поставщиков в соотношении n:m:k. Практика показала, что холодильники этих поставщиков не потребуют гарантийного ремонта с вероятностями равными соответственно р1, р2, р3. Какова вероятность того, приобретенный на фирме холодильник не потребует ремонта в течение гарантийного срока? |
| Вариант 5: n = 4; m = 5; k = 3; р1 = 0,75; р2 = 0,8; р3 = 0,67. Вариант 6: n = 7; m = 4; k = 5; р1 = 0,82; р2 = 0,76; р3 = 0,7. Вариант 7: n = 6; m = 5; k = 4; р1 = 0,85; р2 = 0,7; р3 = 0,65. Вариант 8: n = 7; m = 7; k = 4; р1 = 0,72; р2 = 0,76; р3 = 0,6. | |
| Варианты 9-10 | На конвейер поступают детали с 3-х автоматов. С первого автомата поступает n% продукции, со второго m%, остальные с третьего автомата. Вероятность получения бракованной детали для первого автомата равна р1, второго – р2, третьего – р3. Выбранная случайным образом с конвейера деталь оказалась стандартной. Найти вероятность того, что она поступила с i-го автомата. |
| Вариант 9: n = 25; m = 45; р1 = 0,05; р2 = 0,07; р3 = 0,03; i = 2. Вариант 10: n = 30; m = 35; р1 = 0,06; р2 = 0,04; р3 = 0,05; i = 3. |
Задание 4
| Вариант 1 | Вероятность изготовления на автоматическом станке бракованной детали равна 0,1. Какова вероятность того, что из четырех отобранных деталей стандартных окажется не менее 3? |
| Вариант 2 | Студенты выполняют контрольную работу в компьютерном классе. Работа состоит из 3-х заданий. Для получения положительной оценки необходимо выполнить не менее двух заданий. Для каждого задания зашифровано 4 различных ответа, из которых только один правильный. Студент плохо знает материал и поэтому выбирает ответы наудачу. Какова вероятность того, что он получит положительную оценку? |
| Вариант 3 | Завод производит в среднем 90% изделий высшего сорта, остальные I сорта. Какова вероятность того, что среди 5 наудачу выбранных изделий будет не более одного изделия I сорта? |
| Вариант 4 | При установившемся технологическом процессе автомат производит 70% изделий I сорта и 30% второго. Установить, что является более вероятным – получить три первосортных изделия среди 5 наудачу отобранных или 4 первосортных среди 6 наудачу отобранных? |
| Вариант 5 | Среди изделий, изготавливаемых вручную, в среднем встречается 6% с дефектами. Какова вероятность того, что среди взятых наудачу 5 изделий с дефектами будет не более одного? |
| Варианты 6–10 | На заводе рабочий за смену изготавливает n деталей. Вероятность того, что изготовленная деталь будет удовлетворять стандарту, равна р. Найти вероятность того, что стандарту будет удовлетворять ровно m деталей среди всех произведенных рабочим за смену деталей. |
| Вариант 6: n = 520; р = 0,9; m = 470. Вариант 7: n = 470; р = 0,75; m = 355. Вариант 8: n = 490; р = 0,7; m = 310. Вариант 9: n = 380; р = 0,8; m = 315. Вариант 10: n = 450; р = 0,85; m = 360. |
Задание 5
| Варианты 1–5 | Используя заданное распределение случайной величины Х:
1) построить полигон распределения;
2) вычислить математическое ожидание и дисперсию случайной величины Х;
3) вычислить математическое ожидание случайной величины  . .
| ||||||
| Вариант 1 | Х | а = 3; | |||||
| Р(X=x) | 0,1 | 0,3 | 0,4 | 0,2 | b = -4. | ||
| Вариант 2 | Х | а = -2; | |||||
| Р(X=x) | 0,4 | 0,3 | 0,2 | 0,1 | b = 3. | ||
| Вариант 3 | Х | а = 0,2; | |||||
| Р(X=x) | 0,1 | 0,4 | 0,4 | 0,1 | b = 0,3. | ||
| Вариант 4 | Х | а = -0,3; | |||||
| Р(X=x) | 0,4 | 0,2 | 0,2 | 0,2 | b = 0,4. | ||
| Вариант 5 | Х | а = -0,4, | |||||
| Р(X=x) | 0,2 | 0,2 | 0,4 | 0,2 | b = 0,5. | ||
| Варианты 6-10 | Используя заданное распределение случайной величины Х: 1) вычислить ее математическое ожидание и дисперсию; 2) построить график функции распределения F(x). |
| Вариант 6 | Х | ||||
| Р(X=x) | 0,3 | 0,2 | 0,4 | 0,1 | |
| Вариант 7 | Х | ||||
| Р(X=x) | 0,2 | 0,3 | 0,3 | 0,2 | |
| Вариант 8 | Х | ||||
| Р(X=x) | 0,1 | 0,3 | 0,5 | 0,1 | |
| Вариант 9 | Х | ||||
| Р(X=x) | 0,2 | 0,3 | 0,4 | 0,1 | |
| Вариант 10 | Х | ||||
| Р(X=x) | 0,1 | 0,5 | 0,2 | 0,2 |
Задание 6
| Варианты 1-5 | Непрерывная случайная величина Х задана функцией распределения F(x). Требуется: 1) найти значение параметра С; 2) построить график F(x); 3) вычислить вероятность того, что в результате испытания случайная величина Х примет значение из интервала (; ). |
Вариант 1
 = 4; = 6.
= 4; = 6.
| |
Вариант 2
 = 1; = 2.
= 1; = 2.
| |
Вариант 3
 = 0; = 3.
= 0; = 3.
| |
Вариант 4
 = -2; = 1.
= -2; = 1.
| |
Вариант 5
 = 7; = 9.
= 7; = 9.
| |
| Варианты 6-10 | Непрерывная случайная величина Х задана плотностью вероятности f(x). Определить постоянный параметр С и найти математическое ожидание случайной величины Х. |
Вариант 6

| |
Вариант 7

| |
Вариант 8

| |
Вариант 9

| |
Вариант 10

|
Задание 7
| Варианты 1-7 | Устройства состоит их n независимо работающих элементов, вероятность отказа каждого из которых за время Т равна р. 1) Составить ряд распределения случайной величины Х – числа отказавших элементов за время Т, указав первые k возможных значений. 2) Найти математическое ожидание и дисперсию случайной величины Х. 3) Вычислить вероятность того, что за время Т откажут не менее m элементов. |
| Вариант 1: n = 10000; р = 0,0003; k = 4; m = 3. Вариант 2: n = 20000; р = 0,0001; k = 5; m = 2. Вариант 3: n = 50000; р = 0,00002; k = 4; m = 2. Вариант 4: n = 40000; р = 0,0001; k = 3; m = 3. Вариант 5: n = 25000; р = 0,0002; k = 6; m = 3. Вариант 6: n = 2000; р = 0,002; k = 5; m = 4. Вариант 7: n = 30000; р = 0,0001; k = 5; m = 3. | |
| Варианты 8-10 | В партии из N деталей имеется L нестандартных. Случайным образом выбраны n деталей. 1) Составить ряд распределения случайной величины Х – числа стандартных деталей, среди отобранных. 2) Найти математическое ожидание и дисперсию случайной величины Х. 3) Вычислить вероятность того, что среди выбранных деталей окажется не менее m стандартных деталей. |
| Вариант 8: N = 15; L = 4; n = 4; m = 2. Вариант 9: N = 12; L = 3; n = 3; m = 1. Вариант 10: N = 10; L = 4; n = 3; m = 1. |
Задание 8
| Варианты 1–7 | Пусть Х (час) – время, необходимое для выполнения теста по математике, удовлетворяет показательному распределению с параметром l (час-1). 1). Записать выражение функции распределения F(x) и плотности вероятности f (x). 2). Найти математическое ожидание и дисперсию случайной величины Х. 3). Вычислить вероятность того, что время, необходимое для выполнения теста, не превысит t (час). |
| Вариант 1: l = 0,6; t = 2. Вариант 2: l = 0,3; t = 3. Вариант 3: l = 0,2; t = 4. Вариант 4: l = 0,25; t = 3. Вариант 5: l = 0,35; t = 2. Вариант 6: l = 0,45; t = 3. Вариант 7: l = 0,4; t = 2. | |
| Варианты 8–10 | Времени ожидания поезда метрополитена распределено равномерно в интервале (а; b) (мин). 1). Найти плотность вероятности f (x) и функцию распределения F(x) и построить их графики. 2). Вычислить математическое ожидание и дисперсию случайной величины Х. 3). Вычислить вероятность того, что время ожидания поезда не превысит t (мин). |
| Вариант 8: а = 0; b = 5; t = 4. Вариант 9: а = 0; b = 4; t = 3. Вариант 10: а = 0; b = 3,5; t = 2. | |
Задание 9
Варианты 1-10. По приведенным ниже выборкам:
1) Построить интервальное статистическое распределение.
2) Вычислить выборочное среднее  , моду Мо, медиану Ме, выборочное среднее квадратическое отклонение S.
, моду Мо, медиану Ме, выборочное среднее квадратическое отклонение S.
3) Построить гистограмму относительных частот.
| Вариант 1 | 99,4 | 102,9 | 102,9 | 99,0 | 99,4 | 100,0 | 99,4 | 100,7 | 100,0 | 100,7 |
| Затраты на 100 руб. товарной продукции (в руб.) по предприятиям хлопчатобумажной промышленности за год | 98,4 | 97,1 | 103,7 | 99,4 | 98,4 | 102,9 | 103,4 | 101,5 | 99,4 | 96,8 |
| 100,7 | 101,5 | 100,0 | 104,3 | 100,7 | 102,5 | 103,4 | 101,6 | 99,7 | 97,2 | |
| 102,3 | 100,7 | 100,6 | 102,0 | 98,9 | 102,0 | 102,0 | 102,1 | 100,7 | 102,9 | |
| 102,0 | 102,0 | 98,3 | 100,7 | 102,3 | 103,4 | 101,5 | 101,5 | 100,7 | 104,3 |
| Вариант 2 | 102,3 | 103,4 | 99,0 | 101,5 | 97,8 | 99,0 | 100,5 | 98,4 | 98,4 | 100,5 |
| Затраты на 100 руб. товарной продукции (в руб.) по предприятиям хлопчатобумажной промышленности за год | 102,0 | 101,5 | 102,3 | 97,1 | 100,0 | 100,0 | 105,2 | 100,7 | 99,0 | 102,3 |
| 100,7 | 103,7 | 102,0 | 97,8 | 100,0 | 100,0 | 100,0 | 100,7 | 100,0 | 102,3 | |
| 99,0 | 103,4 | 100,7 | 98,4 | 101,5 | 100,7 | 101,7 | 102,3 | 101,5 | 99,6 | |
| 100,6 | 100,0 | 100,5 | 99,9 | 102,9 | 103,7 | 97,8 | 103,7 | 102,0 | 99,8 |
| Вариант 3 | 0,55 | 0,46 | 0,46 | 0,79 | 0,62 | 0,59 | 0,93 | 0,66 | 0,75 | 0,07 |
| Выпуск товарной продукции на 1 кв. м производственной площади предприятиями (в тыс. руб.) | 0,27 | 0,72 | 0,58 | 0,25 | 0,60 | 1,11 | 0,84 | 0,77 | 0,43 | 0,74 |
| 1,12 | 0,38 | 0,25 | 0,16 | 0,29 | 0,65 | 0,82 | 0,68 | 1,14 | 0,69 | |
| 0,69 | 1,02 | 0,85 | 0,56 | 0,41 | 0,58 | 0,07 | 0,87 | 0,2 | 0,51 | |
| 0,98 | 0,70 | 0,94 | 0,58 | 0,85 | 0,05 | 0,21 | 0,42 | 0,85 | 0,36 |
| Вариант 4 | 0,75 | 0,63 | 0,15 | 0,48 | 0,97 | 0,86 | 0,59 | 1,40 | 0,98 | 0,36 |
| Выпуск товарной продукции на 1 кв. м производственной площади предприятиями (в тыс. руб) | 0,88 | 0,62 | 0,33 | 0,34 | 0,47 | 0,60 | 0,44 | 0,60 | 0,77 | 0,81 |
| 0,77 | 0,42 | 0,75 | 0,57 | 0,38 | 0,78 | 0,73 | 0,12 | 1,03 | 1,21 | |
| 0,26 | 0,95 | 1,10 | 0,18 | 0,65 | 0,68 | 0,48 | 0,44 | 0,92 | 0,39 | |
| 0,67 | 0,62 | 1,07 | 0,78 | 0,03 | 0,82 | 0,87 | 0,91 | 0,61 | 1,05 |
| Вариант 5 | 2,56 | 2,33 | 2,54 | 2,43 | 2,43 | 2,64 | 2,40 | 2,71 | 2,79 | 2,39 |
| Объем основных фондов (млн. руб.) предприятий управления трикотажной промышленности | 2,27 | 2,61 | 2,27 | 2,21 | 2,33 | 2,58 | 2,43 | 2,43 | 2,48 | 2,55 |
| 2,61 | 2,33 | 2,47 | 2,27 | 2,43 | 2,37 | 2,54 | 2,54 | 2,47 | 2,21 | |
| 2,54 | 2,43 | 2,47 | 2,11 | 2,43 | 2,05 | 2,33 | 2,43 | 2,79 | 2,27 | |
| 2,47 | 2,21 | 2,33 | 2,54 | 2,40 | 2,43 | 2,54 | 2,47 | 2,54 | 2,64 |
| Вариант 6 | 2,43 | 2,44 | 2,43 | 2,45 | 2,68 | 2,47 | 2,58 | 2,85 | 2,03 | 2,33 |
| Объем основных фондов (млн. руб.) предприятий управления трикотажной промышленности | 2,64 | 2,12 | 2,27 | 2,68 | 2,37 | 2,47 | 2,61 | 2,54 | 2,21 | 2,64 |
| 2,11 | 2,54 | 2,25 | 2,26 | 2,33 | 2,33 | 3,03 | 2,33 | 2,47 | 2,21 | |
| 2,71 | 2,33 | 2,47 | 2,47 | 2,43 | 2,79 | 2,37 | 2,33 | 3,01 | 2,54 | |
| 2,47 | 2,33 | 2,68 | 2,47 | 2,43 | 2,46 | 2,57 | 2,68 | 2,61 | 2,64 |
| Вариант 7 | 33,8 | 34,8 | 30,4 | 31,4 | 32,6 | 31,4 | 32,4 | 30,4 | 34,2 | 30,8 |
| Оплата труда колхозников (в млн.руб.) одного из колхозов деньгами и натурой за некоторый период времени | 31,2 | 31,2 | 36,2 | 30,4 | 34,0 | 36,0 | 35,2 | 29,6 | 32,4 | 26,5 |
| 32,3 | 31,2 | 30,2 | 29,8 | 32,4 | 29,8 | 32,6 | 32,2 | 30,2 | 32,8 | |
| 33,6 | 36,4 | 30,2 | 36,8 | 31,6 | 32,4 | 31,8 | 33,4 | 35,4 | 29,2 | |
| 32,4 | 35,6 | 36,8 | 29,0 | 32,2 | 33,8 | 30,4 | 32,2 | 31,6 | 32,4 |
| Вариант 8 | 33,6 | 30,8 | 38,1 | 38,1 | 29,6 | 32,2 | 34,2 | 31,6 | 32,2 | 34,0 |
| Оплата труда колхозников (в млн.руб.) одного из колхозов деньгами и натурой за некоторый период времени | 30,4 | 32,0 | 31,0 | 30,4 | 31,4 | 29,0 | 31,2 | 33,2 | 35,0 | 32,4 |
| 30,2 | 32,4 | 33,4 | 36,6 | 29,2 | 33,2 | 33,1 | 28,2 | 33,4 | 31,4 | |
| 33,8 | 32,2 | 29,2 | 29,8 | 26,2 | 29,8 | 33,1 | 34,2 | 32,4 | 32,6 | |
| 31,4 | 32,1 | 36,2 | 30,4 | 32,4 | 23,6 | 30,4 | 33,8 | 33,2 | 32,3 |
| Вариант 9 | 1,9 | 2,8 | 1,9 | 2,5 | 2,4 | 2,2 | 3,0 | 1,9 | 3,0 | 1,7 |
| Производственная площадь (в тыс. кв. м) предприятий управления обувной промышленности | 3,2 | 1,6 | 1,9 | 2,7 | 2,5 | 3,2 | 1,2 | 1,6 | 2,7 | 3,0 |
| 1,9 | 1,7 | 1,9 | 2,2 | 2,2 | 3,4 | 1,6 | 3,2 | 2,2 | 3,0 | |
| 1,6 | 3,0 | 2,5 | 2,85 | 2,5 | 2,5 | 2,2 | 3,2 | 1,2 | 1,9 | |
| 2,2 | 3,0 | 3,8 | 1,4 | 1,6 | 2,7 | 2,2 | 3,4 | 1,6 | 2,5 |
| Вариант 10 | 2,2 | 2,8 | 1,9 | 2,5 | 2,2 | 2,5 | 2,2 | 3,0 | 3,0 | 1,9 |
| Производственная площадь (в тыс. кв. м) предприятий управления обувной промышленности | 3,2 | 1,4 | 1,6 | 2,7 | 2,5 | 3,2 | 1,4 | 1,9 | 2,2 | 1,43 |
| 2,2 | 1,9 | 3,0 | 2,2 | 2,5 | 3,4 | 1,9 | 2,5 | 1,6 | 2,5 | |
| 1,6 | 2,2 | 2,5 | 1,75 | 2,5 | 2,5 | 2,4 | 3,4 | 3,0 | 3,0 | |
| 2,2 | 2,2 | 3,8 | 1,6 | 2,7 | 2,7 | 3,0 | 3,4 | 1,9 | 2,5 |
Методические указания к решению задач
Задание 1
Задача 1.Из ящика, содержащего 20 стандартных и 5 бракованных изделий, извлекаются 2 изделия. Какова вероятность того, что не менее одного изделие окажется стандартным?
Решение. Для решения этой задачи используем классическое определение вероятности

где m – число равновозможных элементарных событий, благоприятствующих появлению события А; n – число всех равновозможных элементарных событий.
По условию задачи m – это число способов, которыми можно выбрать не менее одного изделие стандартного изделия, т.е. 2 стандартных изделия из 20 или 1 стандартное изделие из 20 и 1 бракованное из 5 изделий. Так как порядок выбора изделий не имеет значения, то для вычисления количества комбинаций воспользуемся формулой числа сочетаний
 .
.
Таким образом,
m =  +
+ 
 =
=  = 190 + 205 = 290.
= 190 + 205 = 290.
По условию задачи n – это число способов, которыми можно выбрать 2 изделия из общего количества 25. Следовательно,

Итак,  =
=  0,967.
0,967.
Ответ: Вероятность того, что не менее одного изделия из 25 окажется стандартным, равна 0,967.
Задание 2
Задача 1. Проведены три независимых измерения некоторой физической величины. Вероятность того, что при одном измерении ошибка превысит заданную точность, равна 0,015. Вычислить вероятность следующих событий:
1) В = {только в одном измерении ошибка превысит заданную точность};
2) С = {во всех трех измерениях ошибки не превышают заданную точность};
3) D = {хотя бы в одном измерении ошибка превышает заданную точность}.
Решение. Введем обозначения: событие Ai = {в i-том измерении ошибка не превышает заданную точность}, i = 1, 2, 3.
По условию задачи нам дана вероятность противоположного события. Поэтому для определения вероятности событий Ai воспользуемся тем, что сумма вероятностей противоположных событий равна единице:

1) Теперь составим событие В = {только в одном измерении ошибка превысит заданную точность}, т.е. ошибка превысит заданную точность или только в первом измерении, или только во втором, или только в третьем измерении:
 .
.
Так как события  несовместные и события
несовместные и события  независимые, то вероятность события В равна
независимые, то вероятность события В равна
 ,
,
 .
.
2) Составим событие С = {во всех трех измерениях ошибки не превышают заданную точность}, т.е. событие С состоит в совместном наступлении событий  :
:
 .
.
Вычислим вероятность этого события

3) Для вычисления вероятности события D = {хотя бы в одном измерении ошибка превышает заданную точность} используем вероятность противоположного события  ни в одном из испытаний ошибки не превышают допустимую точность}:
ни в одном из испытаний ошибки не превышают допустимую точность}:
 .
.
Отсюда
 .
.
Вероятность события  равна вероятности события С из пункта 2). Следовательно,
равна вероятности события С из пункта 2). Следовательно,
 .
.
Ответ: Р(В) = 0,0436; Р(С) = 0,956; Р(D) = 0,044.
Задание 3
Задача 1.Два станка-автомата на некоторой фирме производят соответственно 40% и 60% продукции одного вида. Известно, что вероятность брака на 1-м автомате равна 0,06, а на 2-м 0,08. Найти вероятность того, что случайно выбранное изделие окажется годным.
Решение. Для решения данной задачи воспользуемся формулой полной вероятности
Р(А) =  .
.
Обозначим:
А = {изделие годное};
В1 = {изделие изготовлено 1-м автоматом};
В2 = {изделие изготовлено 2-м автоматом}.
Тогда:
P(В1) = 0,4; P(A/В1) = 1 0,06 = 0,94;
P(В2) = 0,6; P(A/В2) = 1 0,08 = 0,92;
По формуле полной вероятности найдем вероятность того, что выбранное изделие окажется годным
P(A) = P(В1) × P(A/В1) + P(В2) × P(A/В2).
Следовательно,
P(A) = 0,4×0,94 + 0,6×0,92 = 0,928.
Ответ: Вероятность того, что случайно выбранное изделие окажется годным,равна 0,928.
Задача 2.На склад поступили приборы с трех заводов в соотношении 2:5:3. Вероятности того, что в течение гарантийного срока прибору потребуется ремонт, для продукции каждого из заводов соответственно равны: 0,3; 0,2; 0,1 . Взятый со склада прибор не имел заводской маркировки и потребовал ремонта в течение гарантийного срока. Какова вероятность того, что прибор изготовлен вторым заводом?
Решение. Для решения данной задачи воспользуемся формулой Байеса
Р(Вi/A) =  .
.
Обозначим:
А = {прибор потребует гарантийного ремонта};
В1 = {прибор изготовлен 1-м заводом};
В2 = {прибор изготовлен 2-м заводом};
В3 = {прибор изготовлен 3-м заводом}.
Так как события В1, В2, В3 образуют полную систему событий, то сумма их вероятностей равна 1. Тогда:
P(В1) =  = 0,2; P(A/В1) = 0,3;
= 0,2; P(A/В1) = 0,3;
P(В2) =  = 0,5; P(A/В2) = 0,2;
= 0,5; P(A/В2) = 0,2;
P(В3) =  = 0,3; P(A/В3) = 0,1.
= 0,3; P(A/В3) = 0,1.
По формуле Байеса, найдем вероятность события В2, при условии наступления события А:
 .
.
Следовательно,
(В2/A) =  0,526.
0,526.
Ответ: Вероятность того, что прибор изготовлен вторым заводом, если известно, что он потребовал ремонта в течение гарантийного срока,равна 0,526.
Задание 4
Задача 1. В магазин вошло 8 покупателей. Найти вероятность того, что или трое или четверо из них совершат покупки, если вероятность совершить покупку для каждого вошедшего одна и та же и равна 0,4.
Решение. Так как количество испытаний невелико (n = 8), то для решения задачи воспользуемся формулой Бернулли
 .
.
По условию n = 8; m1 = 3, m2 = 4; p = 0,4; q = 1 – p = 0,6. Подставим данные в формулу Бернулли
.
Р = Р3,8 + Р4,8 =  =
=
=  0,0640,078 +
0,0640,078 +  0,02560,1296 0,51.
0,02560,1296 0,51.
Ответ: Вероятность того, что или трое или четверо из восьми вошедших покупателей совершат покупку, равна 0,51.
Задача 2. Среди семян ржи 0,4% сорняков. Какова вероятность того, что при случайном отборе 500 семян обнаружиться 5 семян сорняков?
Решение. Количество испытаний велико (  ), а вероятность близка к нулю (
), а вероятность близка к нулю (  ), поэтому воспользуемся формулой Пуассона
), поэтому воспользуемся формулой Пуассона
 ,
,
где  .
.
По условию задачи n = 500, p = 0,004, m = 5.
Тогда  Подставим данные в формулу Пуассона:
Подставим данные в формулу Пуассона:
 .
.
Ответ: Вероятность того, что при случайном отборе 500 семян обнаружиться 5 семян сорняков равна 0,036.
Задача 3. Доля изделий высшего сорта на данном предприятии составляет 30%.
1) Найти вероятность того, что среди 200 выбранных изделий ровно 75 высшего сорта.
2) Найти вероятность того, что в партии из 200 изделий число изделий высшего сорта заключено в интервале от 80 до 120.
Решение. 1) Если число испытаний велико (n = 200), а вероятность появления события в каждом испытании постоянна, то для решения задачи используется локальная теорема Муавра-Лапласа

где  .
.
Для вычисления функции  имеются таблицы (см. Приложения). По условию задачи n = 200; m = 75; p = 0,3; q = 1 – p = 0,7.
имеются таблицы (см. Приложения). По условию задачи n = 200; m = 75; p = 0,3; q = 1 – p = 0,7.
Вычисляем х:

По таблице 1 приложения находим  . Подставив это значение в формулу, получим
. Подставив это значение в формулу, получим

2) Если количество испытаний велико, а вероятность появления события в каждом испытании постоянна, то для вычисления вероятности того, что событие наступит не менее m1 раз и не более m2 раз, используется интегральная теорема Муавра-Лапласа.
P(m1, m2) Ф(x1) Ф(x2),
где  .
.
Для вычисления функции Лапласа Ф(х) имеются таблицы (см. Приложения). По условию n = 200; m1 = 80; m2 = 120, p = 0,3;
q = 1 – p = 0,7.
Вычисляем:

По таблице 2 приложения находим Ф(3,09) = 0,49898, Ф(9,26) = 0,5, т.к.  . Следовательно,
. Следовательно,
P(80, 120) = 0,5 0,49898 = 0,00102.
Ответ: 1)  = 0,0043; 2) P(80; 120) 0,001.
= 0,0043; 2) P(80; 120) 0,001.
Задание 5
| Х | ||||
| Р(Х = хi) | 0,1 | 0,3 | 0,4 | 0,2 |
Задача 1. Закон распределения случайной величины Х имеет следующий вид:
1) Вычислить значения функции распределения  и построить ее график.
и построить ее график.
2) Вычислить математическое ожидание и дисперсию случайной величины  .
.
Решение. 1) Для дискретной случайной величины функция распределения вычисляется по формуле
 .
.
Используя данное распределение, вычислим функцию

Построим график функции распределения:

2) Для того, чтобы вычислить М(Y) и D(Y) воспользуемся свойствами математического ожидания и дисперсии

Осталось вычислить математическое ожидание и дисперсию случайной величины Х, распределение которой известно.
 .
.
Подставив исходные данные в формулу:
 .
.
Дисперсию D(X) вычислим по формуле
 .
.

Тогда, 
Окончательно получим:

Ответ: 2) М(Y) = 15,2, D(Y) = 29,16.
Задача 2. Используя функцию распределения дискретной случайной величины Х, построить ряд распределения этой случайной величины и построить полигон распределения случайной величины Х:

Решение. Для дискретной случайной величины функция распределения вычислялась по формуле
 .
.
Случайная величина Х принимает следующие значения: 1, 3, 5, 7. Используя значения функции распределения, найдем вероятности появления этих возможных значений:
P(X = 1) = 0,3;
P(X = 3) = 0,7 0,3 = 0,4;
P(X = 5) = 0,9 0,7 = 0,2;
P(X = 7) = 1 0,9 = 0,1.
Теперь составим ряд распределения случайной величины Х:
| Х | ||||
| P(X = xi) | 0,3 | 0,4 | 0,2 | 0,1 |
Построим полигон распределения по точкам (xi; рi):

Задание 6
Задача 1. Непрерывная случайная величина Х задана функцией распределения F(x).

Найти:
1) постоянный параметр С;
2) построить график функцией распределения F(x);
3) вычислить математическое ожидание M(X).
Решение. 1) Для определения параметра С воспользуемся свойством функции распределения: если возможные значения случайной величины принадлежат интервалу (a; b), то F(x) = 0 при x  a и F(x) = 1 при
a и F(x) = 1 при
x  b. Следовательно, F(x = 8) = 1:
b. Следовательно, F(x = 8) = 1:
F(x = 8) = С82 = 1, С64 = 1, т. е. С =  .
.
Итак, функция распределения F(x) имеет вид:

2) Построим график функции распределения F(x).

3) Математическое ожидание вычислим по формуле:
 ,
,
где f(x) - плотность вероятности, которую можно вычислить по формуле  . Вычислив производную от функции распределения, получим выражение плотности вероятности:
. Вычислив производную от функции распределения, получим выражение плотности вероятности:

Подставив значение плотности в формулу математического ожидания, получим
 5,33.
5,33.
Ответ: С =  ; M(X) 5,33.
; M(X) 5,33.
Задача 2. Плотность вероятности случайной величины Х задана выражением

Найти:
1) постоянный параметр С;
2) функцию распределения F(x);
3) вероятность того, что в результате эксперимента случайная величина Х примет значение из интервала (0;  ).
).
Решение. 1) Постоянный параметр С найдем из свойства плотности вероятности
 .
.
Так как в данной задаче плотность вероятности случайной величины отлична от нуля на интервале (0;  ), то
), то

Итак,  С = 1, С = 4. Следовательно, плотность вероятности имеет вид:
С = 1, С = 4. Следовательно, плотность вероятности имеет вид:

2) Учитывая свойства функции распределения F(x), сразу определим
F(x) = 0 при x 0; F(x) = 1 при x  .
.
Используя свойство плотности вероятности f(x), найдем функцию распределения F(x) на интервале (0;  ):
):
 .
.

Итак,

3) Для нахождения вероятности  воспользуемся тем, что, если известна функция F(x), то искомая вероятность равна приращению функции F(x) на данном интервале:
воспользуемся тем, что, если известна функция F(x), то искомая вероятность равна приращению функции F(x) на данном интервале:
P(0 < x <