Формула полной вероятности

Рассмотрим следующую задачу.

Пример 3.9. В трех одинаковых ящиках находятся: в первом – 3 белых и 2 черных шара, во втором – 6 белых и 4 черных шара, в третьем – 2 белых и 3 черных шара. Из случайно выбранного ящика наугад вынимается шар. Какова вероятность того, что этот шар белый?

Решение. Пусть событие А означает, что вынутый шар белый. Нетрудно видеть, что вероятность этого события зависит от того, из какого ящика вынимается шар, так как количество белых и черных шаров в ящиках различно. В связи с этим введем в рассмотрение следующие события:

Н₁ – шар вынут из первого ящика;

Н₂ – шар вынут из второго ящика;

Н₃ – шар вынут из третьего ящика.

Так как ящиков только три, то ясно, что события Н₁, Н₂ и Н₃ образуют полную группу (события несовместны, так как выбирается один шар, и в результате испытания: выбор одного шара, одно из этих событий обязательно произойдет). Кроме этого, эти события равновероятны, так как возможность выбора ящика с последующим взятием из него шара одинакова для всех трех ящиков. Таким образом, .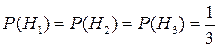

Событие А по условию задачи должно произойти с одним из событий Н₁, Н₂ или Н₃ (шар должен быть вынут либо из первого, либо из второго, либо из третьего ящика). Используя алгебру событий можно событие А записать в следующем виде:

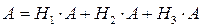Последнее равенство по сути означает, что событие А произойдет тогда, когда белый шар будет вынут из первого ящика (Н₁А) или белый шар будет вынут из второго ящика (Н₂А) или белый шар будет вынут из третьего ящика (Н₃А). Найдем вероятность события А, получим

Последнее равенство следует из очевидной несовместности событий Н₁А, Н₂А и Н₃А. Применим далее теорему умножения вероятностей, тогда

Так как событие А/Н₁ означает, что выбран белый шар при условии, что его выбирают из первого ящика, то вероятность этого события по классической формуле равна . Аналогично можно найти и . Окончательно получаем .

В рассмотренном примере по существу приведен вывод так называемой формулы полной вероятности. Дадим математическую формулировку и доказательство этой формулы.

Теорема 3.7.Пусть Н₁, Н₂, …, Н_n – полная группа событий для некоторого испытания и событие А может произойти вместе с одним из событий полной группы. Тогда справедлива формула

(3.12)

Доказательство. Напомним, что по определению полной группы события Н₁, Н₂, …, Н_n являются несовместными.

По условию теоремы событие А происходит с одним из событий полной группы, следовательно,

Последнее равенство легко понять из следующей геометрической интерпретации:

Н₁ . . . . . . . . . . . . . . . . . . . . . . . . . . . Н₂

. . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . .А . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Н₃ . . . . . . . . . . . . . . . . . . . . . . . . . . . Н₄

Рис.3.1.

Кроме этого, рис.3.1 позволяет понять тот факт, что из несовместности событий Н₁, Н₂, …, Н_n следует и несовместность событий Н₁А, Н₂ А, …, Н_n А. Применяя теорему сложения несовместных событий, а затем теорему умножения вероятностей, получим

Теорема доказана.

Формула (3.12) носит название формулы полной вероятности, а события Н₁, Н₂, …, Н_n называются гипотезами.

Формула полной вероятности применяется в тех случаях, когда само испытание как бы распадается на два этапа: на первом этапе определяются возможные условия опыта, т.е. гипотезы, на втором происходит сам опыт одновременно с какой-то гипотезой.

Пример 3.10. Для приема зачета преподаватель подготовил 50 задач: 20 задач по дифференциальному и 30 задач по интегральному исчислению. Для получения зачета студент должен решить первую попавшуюся ему задачу. Какова вероятность для студента получить зачет, если он знает решение 18 задач по дифференциальному и 15 по интегральному исчислению?

Решение. Пусть событие А означает, что студент получит зачет, т.е. решит предложенную ему задачу. Задача может быть по одной из двух тем, поэтому гипотезами будут следующие события: Н₁ – получена задача по дифференциальному исчислению; Н₂ – получена задача по интегральному исчислению.

Так как по условию задачи имеется 20 задач по дифференциальному и 30 задач по интегральному исчислению, то

и .

Событие А/Н₁ означает, что студент решит задачу, если эта задача по дифференциальному исчислению, следовательно,

Событие А/Н₂ означает, что студент решит задачу, если эта задача по интегральному исчислению, следовательно,

По формуле (3.12) получим

Формулы Байеса

Обратимся к примеру 3.9 и несколько изменим его условие.

Пример 3.11. В условиях примера 3.9, предположим, что шар вынут и известно, что он оказался белым, т.е. событие А произошло. Какова вероятность того, что шар был вынут из первого ящика?

Таким образом, требуется найти вероятность того, что шар был вынут из первого ящика, если он оказался белым, т.е. Р(Н₁/А). Необходимо различать две вероятности: Р(Н₁) и Р(Н₁/А). Уточним их смысл.

Р(Н₁) – вероятность того, что шар будет вынут из первого ящика, т.е вероятность события Н₁, вычисленная до испытания.

Р(Н₁/А) – вероятность того, что шар был выбран из первого ящика, если он оказался белым, т.е. вероятность события Н₁, вычисленная при условии, что событие А уже произошло или, иначе, вероятность, вычисленная после опыта.

Аналогичные вероятности могут быть получены и для остальных гипотез Н₂ и Н₃ в примере и для Н_i , i = 1, 2, …, n в общем случае.

Вероятности гипотез Р(Н_i), i = 1, 2, …, n называются априорными вероятностями, т.е. «доопытными».

Условные вероятности гипотез Р(Н_i/A), i = 1, 2, …, n называются апостериорными вероятностями, т.е. «послеопытными».

Итак, в результате решения подобного рода задач, известные до опыта априорные вероятности гипотез Р(Н_i)подвергаются переоценке после того, как в результате испытания произошло событие А, т.е. происходит переход к апостериорным вероятностям гипотез Р(Н_i/A).

Выведем общую формулу для условных вероятностей гипотез.

Пусть Н₁, Н₂, …, Н_n – полная группа событий (гипотезы) для некоторого испытания. Событие А может произойти вместе с одним из событий полной группы, следовательно, . По теореме умножения вероятностей (формулы (3.8)) получим

, i = 1, 2, …, n.

Левые части последних равенств равны, следовательно, равны и их правые части, т.е.

Отсюда, с учетом того, что , получаем

(3.13)

или, применяя к знаменателю формулу (3.12):

(3.14)

Формулы (3.13) и (3.14) называются формулами Байеса.

Формулы Байеса позволяют определить для любого события А, вероятность которого не равна нулю, условную вероятность Р(Н_i/A), когда известно, что событие А уже произошло в результате испытания.

Заметим, что имеет место формула

так как события, вероятности которых суммируются в левой части предлагаемой формулы, образуют полную группу событий для данного испытания.

Вернемся к примеру 3.11 и найдем вероятность того, что шар был вынут из первого ящика:

Пример 3.12. 30% кинескопов, имеющихся на складе, изготовлены на заводе №1, остальные – на заводе №2. Вероятность того, что кинескоп, изготовленный на заводе №1, не выйдет из строя в течение гарантийного срока службы, равна 0,9, для кинескопов с завода №2 эта вероятность равна 0,8. Случайным образом для проверки со склада выбрали кинескоп, который выдержал гарантийный срок. Определить вероятность того, что его изготовили на заводе №2.

Решение. В условиях примера известно, что опыт произошел, т.е кинескоп выбран со склада и исследована его работа в течение гарантийного срока службы. Обозначим через А событие, состоящее в том, что кинескоп выдержит гарантийный срок службы. Гипотезами будут следующие события:

Н₁ – кинескоп изготовлен на заводе №1;

Н₂ – кинескоп изготовлен на заводе №2.

Так как 30% кинескопов изготовлены на заводе №1 и, следовательно, 70% изготовлены на заводе №2, то Р(Н₁) = 0,3 и Р(Н₂) = 0,7.

По условию Р(A/Н₁) = 0,9 и Р(A/Н₂) = 0,8, следовательно, полная вероятность события А равна

И, наконец, . Нетрудно сообразить, что .

Формулы Байеса находят широкое применение. В книге Б.В.Гнеденко и А.Я.Хинчина «Элементарное введение в теорию вероятностей» показано применение этих формул в артиллерийской практике, где производится так называема пристрелка, имеющая цель – уточнить наши знания об условиях стрельбы. На основе результатов нескольких пробных выстрелов ставится задача о вычислении новых вероятностей гипотез, связанных с поражением некоторой цели. Однако формулы Байеса широко применяются и при решении многих других, в том числе и экономических, задач.

В общем случае формулы Байеса могут применяться в следующей ситуации. Пусть рассматривается некоторое событие или явление, которое может происходить при некоторых условиях-предположениях (гипотезах). Предположений несколько и они взаимно исключают друг друга. Как правило, до опыта возможность появления тех или иных условий, того или иного предположения неизвестна. Поэтому вероятность каждого предположения или гипотезы до опыта определяется интуитивно или на основе каких-то общих рассуждений. После проведения опыта эти интуитивно найденные вероятности уточняются на основании результата опыта. Необходимо отметить, что опыт можно повторить и провести дальнейшее уточнение вероятностей гипотез. Так, например, если решается какая-то экономическая задача с недостаточной информацией, то по мере расширения информации может быть проведена и корректировка найденного ранее решения.