Постановка задачи и метод решения.

Курсовая работа

по дисциплине «Прикладное программное обеспечение
для математических исследований»

на тему:

«Моделирование физических процессов в твёрдых телах»

 

Студент: Ильина Галина Александровна

Группа: ТМБО-01-13(ВТ-11), 4 курс

Форма обучения: дневная

Доля авторского текста (оригинальности)

в результате автоматизированной проверки составила ______%.

Работа защищена на оценку ____________ «___» _____________ 2016 г.

 

Преподаватель: к.ф.-м.н., доцент Шмелева А. Г.

 

Москва, 2016 г.

 

Оглавление

1 Введение……………………………………………………………………..…3

2 Задания………………………………………………………………...……. . ..5

3 Задача Коши…………………………………………………............................9

4 Листинг программы прогонки…………………………………………..…..13

5 Задача Дирихле для уравнения Лапласа …………………………………....15

6 Листинг программы ………………………………………………………....21

7 Вывод………………………………………………………………………....22

8 Список используемых источников………………………………………….23

 

 

Введение

Прикладное программное обеспечение (ППО) составляют программы конечного пользователя. Это самый обширный класс программного обеспечения. В настоящее время в большинстве сфер человеческой деятельности разработаны и применяются прикладные программные продукты. Везде, где требуется выполнить большие математические расчеты или производится обработка больших объемов разнообразных данных, или требуется быстрый анализ ситуации с принятием управляющего решения, – компьютеры под управлением прикладного программного обеспечения с успехом заменяют человека.
Прикладное программное обеспечения специального назначения используется для более узких задач, а также задач профессионального характера. К ним относятся СУБД информационных систем, программные средства для решения математических задач, экспертные системы и т.д. Рассмотрим программные средства для решения математических задач. Существуют различные программы для решения математических задач такие как Scilab, Maple, Matcad и другие. В этих программах выделяются различные операции: вычисление выражения в аналитическом и в комплексном виде, разложения в ряд, преобразования Лапласа, пределы, интегрирования и другие операций, включающие в эти программы. В данной курсовой работе рассмотрим два задания. В первом задание рассмотрим задачу Коши, решим задачу методом прогонки и вычислим точное решение. Целью данной работе будет подробное решение задачи Коши аналитическим методом, а так же методом прогонки, предварительно запрограммированном в системе wxMaxima.

Хочется заметить что задача Коши очень похожа на обыкновенное решение дифференциальных уравнений, основная разница заключается в том, что в нашей задаче требуется отыскать частное решение, такое решение которое будет удовлетворять какому то конкретному условию поставленной нам задачи.

Одной из интереснейших задач теории дифференциальных уравнений (обыкновенных и с частными производными) является задача Коши, цель которой сводится к поиску правильного решения (интеграла) дифференциального уравнения, удовлетворяющего данным нам изначально так называемым начальным условиям (начальным данным).
Задача Коши в большинстве случаев предстаёт перед нами при пристальном рассмотрении анализа процессов, построенных на основании дифференциального закона эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие).

Во втором задание рассмотрим задачу Дирихле для уравнения Лапласа на прямоугольнике методом конечных разностей. Для решения использовать явную трёхслойную схему «крест». Построить диаграмму распределения значений функции в виде линий уровня. В итоге мы получим пять линейных векторных уравнений с пятью неизвестными векторами.

 

 

Задания

Задание № 1.

1.Решить аналитически задачу Коши. Варианты взять из таблицы 1. Краевое условие в точке b: y(b)=B вычислить, решив аналитически соответствующую задачу Коши:

 

 

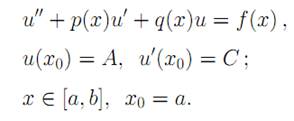
после нахождения точного решения поставить в него точку b=1, т.е. В=y(1)).

Значения a и b во всех вариантах равны 0 и 1, соответственно [a,b]=[0,1].

 

2. Решить задачу методом прогонки, шаг h=(b-a)/n.

3. Вычислить точное решение с тем же шагом и величину .

 

 

Таблица 1- Исходные данные

Задание № 2.

Формулировка задачи: решить задачу Дирихле для уравнения Лапласа на прямоугольнике методом конечных разностей с шагом по осям x и y соответственно hx и hy.,а uл , uп , uн , uв - соответственно значения функции на левой, правой, нижней и верхней сторонах прямоугольника. Для решения использовать явную трёхслойную схему «крест». Построить диаграмму распределения значений функции в виде линий уровня.

 

Вариант	A	b	hx	hy	uл	uп	uн	uв
		1.2		0.2

 

Задача 1

 

Постановка задачи и метод решения.

.

Уравнение

,

является линейным неоднородным уравнение второго порядка с постоянными коэффициентами. Его общее решение имеет вид

,

где – общее решение соответствующего однородного уравнения , а – произвольное решение уравнения (1.2).

Характеристическим уравнением для однородного уравнения является . Его корни . Следовательно, общее решение уравнения имеет вид . Таким образом,

.

Согласно общей теории линейных дифференциальных уравнений с постоянными коэффициентами, правая часть уравнения (1.2) имеет специальный вид. Будем искать частное решение как

.

 

 

Дифференцируя данное выражение

 

Находим, что . Приравнивая правую часть полученного выражения к правой части уравнения (1.2), находим, что . Таким образом, мы нашли частное решение уравнения (1.2) в виде .

Согласно формулам (1.3) и (1.4), общее решение уравнения (1.2) имеет вид

Имея данное общее решение легко получить решение задачи Коши (1.1).

Очевидно, что и . То есть .

Итак, решение задачи Коши (1.1): .

 

Метод прогонки.

Найдем приближенное решение задачи (1.1) на отрезке с шагом .

Соответствующая разностная схема имеет вид.

 

 

где – номера узлов, – искомые значения аппроксимирующей функции в узлах, . Напомню, что последняя функция является функцией из условия.

 

Перепишем схему в виде.

 

(2.1)

 

Значения и нам известны, поэтому нам нужно решить линейную неоднородную систему из 9 уравнений (2.1).

 

Приведем ее к виду, пригодному к методу прогонки. Именно, перепишем первое и последнее уравнения:

 

(2.2)

 

где , и для остальных индексов.

Результатом метода прогонки, примененной к данной системе, являются соотношениями

 

,

 

в которых числа определяются соотношениями.

 

 

Далее приведены соответствующие массивы.

Таблица 1-массивы

		2.1207	2.2847	2.4955	2.7574	3.0751	3.454	3.9003	4.421	5.024	5.7183
		2.1205	2.2843	2.495	2.7567	3.0744	3.4533	3.8996	4.4204	5.0236	5.7183
Модуль разности		0.0002	0.0004	0.0006	0.0007	0.0007	0.0007	0.0007	0.0005	0.0003

 

 

Графики практически сливаются

Рисунок 1- Значения в узлах приближенного и точного решений значения в узлах приближенного и точного решений

 

 

Листинг программы прогонки в системе wxMaxima

В последней таблице (окно результатов) первая и вторая колонки – это значения в узлах приближенного и точного решений. Последний столбец – абсолютные величины их разностей. Параметр здесь не число интервалов аппроксимации, а число узло. В силу специфики программной среды – индексы начинаются с 1 – они сдвинуты, то есть , и т.д. Значения точного решения в точках сетки обозначены .

 

 

 

Задача 2