Графический метод решения ЗЛП

 

Рассмотрим ОЗЛП (1)-(5) с геометрической точки зрения.

Всякую упорядоченную совокупность n чисел x₁, …, x_n можно рассматривать как точку или вектор n-мерного пространства.

В связи с этим и планы ЗЛП будем трактовать как точки n-мерного пространства.

Они образуют выпуклое множество.

 

Выпуклым называется множество, которое вместе с любыми своими точками х₁ и х₂ содержит также и все точки х отрезка х₁х₂ (рис. 2), т.е. точки вида х = х₁ + (1-)х₂, где 0 1, т. е. вместе с любыми точками х₁ и х₂ множество содержит их произвольную выпуклую линейную комбинацию.

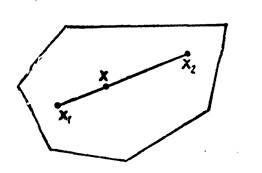
Рисунок 2

 

Теорема 2. Множество планов ОЗЛП является выпуклым.

 

Множество м.б. ограниченным или неограниченным.

Множество точек х называется ограниченным, если существует такое М>0, что для всех точек, принадлежащих множеству, х М.

В противном случае множество называется неограниченным.

 

Множество планов ЗЛП м.б. ограниченным (выпуклый многогранник, рис. 3, а) или неограниченным (выпуклая многогранная область, рис. 3, б), м.б. единственной точкой (рис. 3, в) или пустым множеством (рис. 3, г), прямой линией или лучом, отрезком прямой.

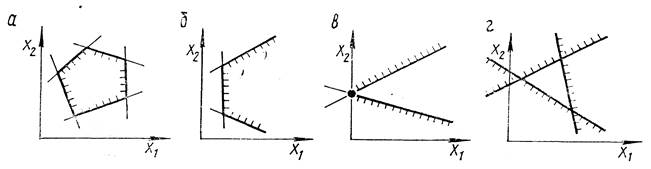
Рисунок 3

 

Множество точек (х₁, …, х_n), координаты которых удовлетворяют уравнению а₁х₁+…+а_nx_n = a, называют гиперплоскостью.

В связи с этим целевую функцию (1) в записи с₁х₁+…+с_nx_n = f геометрически можно рассматривать, как семейство параллельных гиперплоскостей, каждой из которых соответствует определённое значение р функции f (рис. 5).

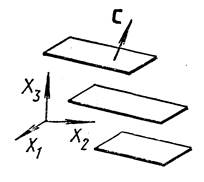
Рисунок 5

 

Вектор с = (с₁; …; с_n), перпендикулярный к гиперплоскостям, указывает направление наискорейшего возрастания функции f.

Поскольку в любой точке каждой гиперплоскости функция f принимает одно и тоже значение (сохраняет значение на постоянном уровне), то их называют плоскостями уровня.

 

Формулировка ЗЛП на геометрическом языке:

найти точку х^* = (х^*₁; …; х^*_n) многогранника планов, определяемого системой (2)-(5), через которую проходит гиперплоскость семейства (1), соответствующая наибольшему (наименьшему) значению функции f.

В частности, при n = 2 и ограничениях-неравенствах модель ЗЛП имеет вид:

Геометрически задача (31)-(33) формулируется так:

найти точку х^* = (х^*₁, х^*₂) многоугольника (многоугольной области) планов, определяемого системой (32)-(33), через которую проходит прямая семейства (31), соответствующая наибольшему (наименьшему) значению функции f (рис. 6).

Прямые f = const являются линиями уровня.

Рисунок 6

 

Используя данную интерпретацию, можно предложить следующий порядок графического решения задачи (31)-(33) (рис. 7):

1) построить многоугольник (многоугольную области) планов;

2) построить вектор с = (с₁, с₂) и одну из прямых семейства f= const, например f = 0;

3) параллельным перемещением прямой f = 0 в направлении вектора с (-с) найти точку А_max (B_min), в которой f достигает максимума (минимума);

4) решая совместно уравнения прямых, пересекающихся в точке оптимума, найти ее координаты, а затем f_max (f_min).

Рисунок 7

 

В зависимости от особенностей области планов (ограничена или нет) и взаимного расположения области и вектора с возможны различные случаи (рис. 8).

На рисунке 8, а функция достигает минимума в единственной точке А, а максимума – в любой точке отрезка ВС; на рис. 8, б максимум достигается в точке А, минимума функция не имеет (f -); на рис. 8, в функция не имеет ни максимума (f +) ни минимума (f -).

 

Рисунок 8

Вывод: если целевая функция ЗЛП достигает оптимума, то это имеет место по крайней мере в одной из вершин области планов.

 

Пример.

Найти максимум или минимум функции f = х₁ + 3х₂ при условиях

Решение.

Построим допустимую область. Каждое из неравенств определяет некоторую полуплоскость вместе с граничной прямой, уравнение которой получается заменой знака неравенства на знак равенства.

Общая часть этих полуплоскостей и образует допустимую область.

Чтобы установить, какая же из двух полуплоскостей, на которые граничная прямая делит плоскость х₁Ох₂, является решением данного неравенства, надо подставить в него координаты какой-либо точки, лежащей по ту или другую сторону от граничной прямой.

Если они удовлетворяют данному неравенству, то искомой будет полуплоскость, в которой расположена взятая точка; если же неравенство не удовлетворяется, то искомой будет другая полуплоскость.

Построив граничную прямую 1 по уравнению 3х₁ + 2х₂ = 6, подставим в неравенство 3х₁ + 2х₂ 6 координаты, например, точки О (0; 0): 3·0+2·06 или 0<6.

Видим, что координаты точки О (0; 0) удовлетворяют неравенству.

Следовательно, данному неравенству соответствует полуплоскость, в которой лежит точка О.

Построив прямые 2 и 3 соответственно по уравнениям х₁=0,5 и х₂ = 1, аналогично определяем и другие полуплоскости, соответствующие остальным неравенствам, а затем и пересечение всех найденных полуплоскостей – многоугольник АВСD, являющийся областью допустимых решений задачи.

Далее строим вектор с = (с₁; с₂) = (1; 3) и линию уровня f = 0, перпендикулярную к нему.

После этого параллельным перемещением вспомогательной прямой f = 0 находим точку А(1/2; 0) (см. прямую f_min), в которой функция достигает минимума f_min = 0,5, и точку С (4/3; 1) (см. прямую f_max), где f имеет максимум f_max = 4,33.

end.

 

Пример 2.

Найти графическим методом максимум функции f = х₁ + х₂ при условиях

х₁ + х₂ -1;

х₁ 0;

х₂ 0;

Решение:

 

Условие неотрицательности переменных означает, что множество допустимых планов должно лежать в неотрицательном квадранте.

Линейное неравенство х₁ + х₂ -1 определяет полуплоскость, лежащую ниже прямой, задаваемой аналитически уравнением х₁ + х₂ -1.

Эта полуплоскость не имеет общих точек с неотрицательным квадрантом (рисунок Х), значит, множество допустимых планов пусто и задача не имеет решения.

 

Пример 3.

Найти графическим методом максимум функции f = х₁ + х₂ при условиях

х₁ - х₂ 1;

х₁ 0;

х₂ 0;

 

 

Пример 4.

 

Найти графическим методом максимум функции f = х₁ + х₂ при условиях

х₁ + 2х₂ 1;

2х₁ + х₂ 1;

х₁ 0;

х₂ 0;

Решение:

В этом примере множество допустимых планов Х представляет собой пересечение положительного квадранта и двух полуплоскостей, ограниченных сверху прямыми, задаваемыми уравнениями х₁ + 2х₂ 1; 2х₁ + х₂ 1; (рисунок )

Т. к. множество Х замкнуто и ограничено, а целевая функция непрерывна, то задача имеет решение.

Линия наивысшего уровня функции х₁ + х₂ на многограннике Х проходит через вершину с координатами х⁰₁ + х⁰₂ = 1/3.

Это и есть решение задачи.

 

Пример 5.

Найти графическим методом максимум функции f = х₁ + х₂ при условиях

х₁ + 2х₂ 1;

2х₁ + х₂ 1;

х₁ + х₂ 3/5;

х₁ 0;

х₂ 0;

 

Решение:

Решение задачи заполняет отрезок [А, В], включая в том числе две вершины допустимого многогранника А и В.