Свойства алгебраических операций

Известно, что сложение и умножение чисел обладает свойствами коммутативности, ассоциативности, умножение дистрибутивно относительно сложения. Аналогичными свойствами обладают объединение и пересечение множеств.

Рассмотрим свойства алгебраических операций, определив их в общем виде. При этом условимся алгебраические операции обозначать символами: * (читается - «звездочка») и (читается - «кружок»).

Важнейшим свойством алгебраических операций является свойство ассоциативности.

Определение. Алгебраическая операция *, заданная на множестве X, называется ассоциативной, если для любых элементов x,y и z из множества X выполняется равенство

(x*y)*z =x*(y*z).

Если операция * обладает свойством ассоциативности, то можно опускать скобки и писать x*y*z вместо (x*y)*z и х+(y*z).

Например, ассоциативно сложение натуральных чисел: для любых натуральных чисел х, у и z выполняется равенство (х + у) + z = х + (у + z). Ассоциативно сложение рациональных и действительных чисел. Поэтому сумму нескольких чисел можно записывать без скобок.

Существуют алгебраические операции, не обладающие свойством ассоциативности. Так, не является ассоциативным вычитание целых чисел: существуют целые числа х, у и z, для которых (х -у) – z х - (у - z). Например, (12 - 7) - 3 12 - (7 - 3).

Ассоциативность алгебраической операции позволяет записывать без скобок все выражения, содержащие лишь эту операцию, но переставлять входящие в это выражение элементы, вообще говоря, нельзя. Перестановка элементов возможна лишь в случае, когда операция * коммутативна.

Определение. Алгебраическая операция * на множестве X называется коммутативной, если для любых двух элементов х и у из множества X выполняется равенство

х*у =у*х.

Примерами коммутативных операций могут служить сложение и умножение натуральных чисел, поскольку для любых натуральных чисел х и у выполняются равенства х + у = у + х, ху = ух. Эти равенства справедливы не только для натуральных чисел, но и для любых действительных чисел, следовательно, на множестве действительных чисел сложение и умножение тоже коммутативны.

Существуют алгебраические операции, не обладающие свойством коммутативности. Так, не является коммутативным вычитание целых чисел: существуют целые числа хну, для которых х – у у - х. Например, 12-7 7-12.

Если на множестве X заданы две алгебраические операции * и , то они могут быть связаны друг с другом свойством дистрибутивности.

Определение. Алгебраическая операция называется дистрибутивной относительно алгебраической операции *, если для любых элементов х, у и z из множества X выполняются равенства:

1) (х*у) z = (z x)*(z y) и 2) z(х*z)=( zх) *(zу).

Если выполняется только равенство 1), то операцию называют дистрибутивной справа относительно операции *; если же выполняется только равенство 2), то операцию называют дистрибутивной слева относительно операции *.

Выясним, в каких случаях различают дистрибутивность справа и слева.

Рассмотрим на множестве натуральных чисел две операции возведение в степень (она соответствует операции в равенствах 1 и 2) и умножение (она соответствует операции * в равенствах 1 и 2). Тогда, согласно равенству 1, имеем: (ху)^z= х^zу^z. Как известно из алгебры, полученное равенство справедливо для любых натуральных чисел х,у и z, т.е. возведение в степень дистрибутивно справа относительно умножения. В соответствии с равенством 2, получаем x^yz = x^yx^z. Но это равенство выполняется не всегда, т.е. операция возведения в степень не является дистрибутивной слева относительно умножения. Такая ситуация является следствием того, что возведение в степень - операция, не обладающая свойством коммутативности.

Если взять сложение и умножение натуральных чисел, то, как известно, умножение дистрибутивно относительно сложения: для любых натуральных чисел х, у и z выполняются равенства

(x + y) z = xz + yz и z(x + y) = zx + zy.

А так как умножение коммутативно, то не имеет значения, где писать множитель z - справа от суммы х + у или слева от нее. Поэтому в школьном курсе математики не различают дистрибутивность слева и справа, а говорят просто о дистрибутивности умножения относительно сложения.

Выясним роль свойства дистрибутивности в преобразованиях выражений. Если операция о дистрибутивна относительно операции * и обе операции ассоциативны, то в любом выражении, содержащем лишь эти две операции, можно раскрыть все скобки, перед которыми (или за которыми) стоит знак . Проиллюстрируем сказанное на примере преобразования выражения (х + y) (z + p). Так как умножение дистрибутивно относительно сложения, то

(x+y) (z+p) = x (z+p) + y (z+p) = (xz+xp) + (yz+yp).

А поскольку сложение ассоциативно, то последнюю запись можно записать без скобок. Следовательно, (x+y) (z+p) = xz+xp+yz+yp.

Часто в множестве, на котором рассматривается алгебраическая операция, выделяются особые элементы, называемые в алгебре нейтральными и поглощающими.

Определение. Элемент е из множества X называется нейтральным относительно алгебраической операции *, если для любого элемента х из множества X выполняются равенства х*е =е*х =х.

Доказано, что если нейтральный элемент относительно алгебраической операции существует, то он единственный.

Определение. Элемент р из множества X называется поглощающим относительно алгебраической операции *, если для любого элемента х из множества X выполняются равенства х*р =р*х=р.

Если поглощающий элемент относительно алгебраической операции существует, то он единственный.

Так, в множестве Z целых неотрицательных чисел нуль является нейтральным элементом относительно сложения, поскольку для любого х из множества Z выполняются равенства x + 0 = 0 + x = х. Это же число нуль является поглощающим элементом относительно умножения: для любого х из множества Z верны равенства: х0 = 0х = 0.

Как известно, вычитание чисел является операцией, обратной сложению. Но чтобы дать определение обратной операции в общем виде, надо определить понятие сократимой операции.

Определение. Алгебраическая операция *, заданная на множестве X, называется сократимой, если из условий а*х = а*у и х*а = у*а следует, что х =у.

Например, сократимо сложение натуральных чисел: из равенства а+х=а+у и х+а=у+а следует, что х = у.

Определение. Пусть * - сократимая и коммутативная алгебраическая операция, заданная на множестве X. Тогда операция называется обратной для операции *, если х у = z тогда и только тогда, когда y*z=x.

Тот факт, что вычитание на множестве целых чисел есть операция, обратная сложению, означает: z = х - у тогда и только тогда, когда у + z = х.

Множество X с заданными на нем алгебраическими операциями принято называть алгеброй. В начальном курсе математики в основном изучают множество Z целых неотрицательных чисел, которое является объединением натуральных чисел и нуля: Z_o = N {0}. На этом множестве рассматриваются алгебраические операции сложения и умножения. Используя язык современной математики, можно сказать, что в начальной школе изучают алгебру (Z_o, +, ). Ее основные характеристики:

1) Сложение и умножение на множестве Z_o ассоциативно и коммутативно, а умножение дистрибутивно относительно сложения, т.е.:

( х, у 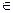Z_o) x + у=у + х;

( х,y 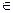Z_o) ху = ух;

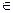( x,y,z Z_o) (x + y) + z = x + (y + z);

( x,y,z 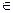Z_o) (xy) z = x (yz)

( x,y,z 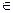Z_o) (x + y) z = xz + yz

2) Сложение и умножение сократимы (исключая сокращение произведения на нуль), т.е. для любых целых неотрицательных чисел х,у и а справедливы утверждения:

х+а=у+а х=у

ха=уа х=у

3) Нуль является нейтральным элементом относительно сложения и поглощающим относительно умножения:

( х 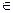Z_o) х + 0 = 0 + х = х;

( х Z_o) x0 = 0x = 0.

Единица является нейтральным элементом относительно умножения:

( х 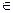Z_o) х1 = lx = x.

4) Сократимость сложения и умножения целых неотрицательных чисел позволяет определить в Z_o частичные алгебраические операции вычитания и деления как обратные соответственно сложению и умножению (исключая деление на нуль):

х-у =z <=> у + z = х

х:у = z <=> yz = х.

5) Вычитание и деление обладают свойствами:

Названные характеристики алгебры (Z_o, +, ) присутствует (явно или неявно) в любом начальном курсе математики.